Курсовая работа по дисциплине ТЭС. Курсовая ТЭС. Расчёт основных характеристик цифровой системы связи с использованием квадратурной модуляции
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
ДекодерТребуется: 1. В соответствии с табл. 2, полученной для этого варианта в разд. 4.3, выписать из 2-й строки численные значения кодовых символов (КС), которые передавались по каналу связи. Из табл. 1 исходных данных определить номер тактового интервала 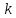 , на котором произошла ошибка на выходе демодулятора, т. е. , на котором произошла ошибка на выходе демодулятора, т. е. 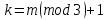 . . 2. Построить решетчатую диаграмму декодера с учетом полученной последовательности 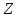 . Построить диаграммы выживших путей от момента времени . Построить диаграммы выживших путей от момента времени 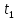 до момента времени до момента времени 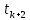 по аналогии с решетчатыми диаграммами, когда от момента по аналогии с решетчатыми диаграммами, когда от момента 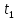 до момента до момента 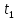 выживает только один путь. выживает только один путь.3. Построить диаграммы выживших путей. Определить момент времени 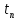 , когда останется только один выживший путь. Этот путь с решетчатой диаграммы декодера перенести на решетчатую диаграмму кодера и по этой диаграмме определить кодовые символы (КС), которые действительно передавались по каналу связи. Перенести один выживший путь от момента времени , когда останется только один выживший путь. Этот путь с решетчатой диаграммы декодера перенести на решетчатую диаграмму кодера и по этой диаграмме определить кодовые символы (КС), которые действительно передавались по каналу связи. Перенести один выживший путь от момента времени 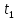 до момента до момента 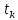 с решетчатой диаграммы декодера на решетчатую диаграмму кодера. По этому пути на диаграмме кодера определить те кодовые символы, которые поступали на вход сверточного кодера и передавались по каналу связи от момента с решетчатой диаграммы декодера на решетчатую диаграмму кодера. По этому пути на диаграмме кодера определить те кодовые символы, которые поступали на вход сверточного кодера и передавались по каналу связи от момента 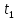 до момента до момента 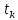 . .В результате этой операции ошибка, полученная на выходе демодулятора, будет исправлена. Численные значения кодовых символов будут записаны следующим образом: 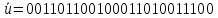 (73) (73)Определим номер тактового интервала 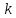 , на котором произошла ошибка: , на котором произошла ошибка: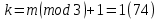 Это значит, что ошибка произошла на первом тактовом интервале. Таким образом, последовательность ошибок примет вид: 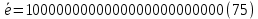 Поэтому с демодулятора на декодер будет поступать последовательность кодовых символов 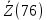 : :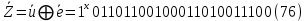 Ошибку необходимо исправить. Неправильно принятый бит отметим крестиком. Решётчатая диаграмма декодера изображена на рис.33.  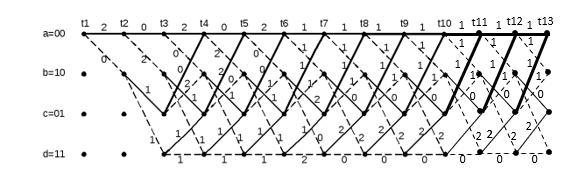 Рис. 33 Решётчатая диаграмма декодера  10 11 01 10 01 00 01 10 10 01 11 00                                                                                        1 1 2 0 0 2 1 2 0 1 2 0 1 1 1 1 2 1 1 1 0 1 1 1 1 1 1 0 1 1 1 1 0 1 1 1 1 1 1 1 1 1 1 0 2 2 0 1 0 2 0 1 1 0 2 2 0 1 0 2 1 1 1 2 0 0 2 1 2 0 2 0 0 1 1 1 1 0 1 1 1 0 2 1 1 1 1 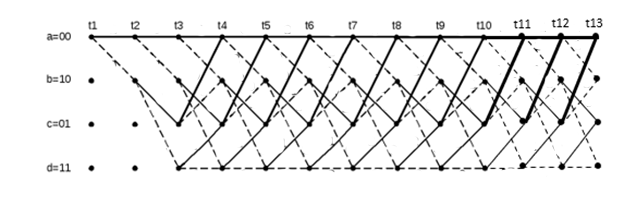 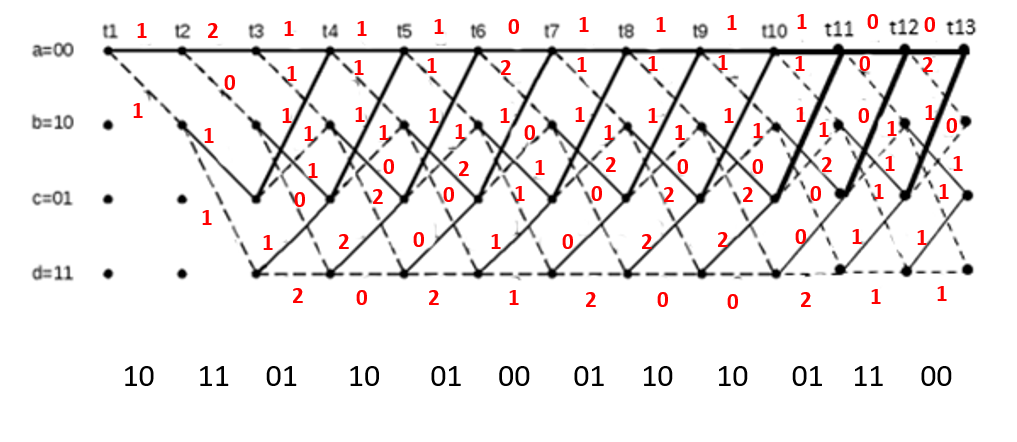         10 11 01 10 01 00 01 10 10 01 11 00  |
