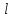Курсовая работа по дисциплине ТЭС. Курсовая ТЭС. Расчёт основных характеристик цифровой системы связи с использованием квадратурной модуляции
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
Исходные данныеТаблица 1
Источник сообщенияТребуется: Написать аналитические выражения для плотности вероятности w(a) мгновенных значений сообщения, функции распределения F(a) и построить их графики; Рассчитать математическое ожидание A(t) и дисперсию DA(t) сообщения A(t); Написать аналитическое выражение для спектральной плотности мощности GA(f) сообщения A(t) и построить график; Найти аналитическое выражение для корреляционной функции BA(τ) сообщения A(t) и построить график. По форме графика BA(τ) определить, является ли сообщение A(t) эргодическим случайным процессом или не является таковым; 1) Для того, чтобы рассчитать функцию плотности распределения вероятностей w(a), необходимо воспользоваться условием нормировки, которое имеет вид: 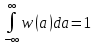 (1) (1)Это равенство показывает, что площадь ограничения кривой w(a) от 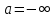 до до 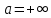 будет рана единице. будет рана единице.Поскольку появление мгновенных значений случайного процесса A(t) является равновероятным на интервале ( 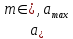 ), то это означает, что функция w(a) является равномерной. Это значит, что она рана постоянной величине C на интервале ( ), то это означает, что функция w(a) является равномерной. Это значит, что она рана постоянной величине C на интервале (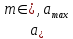 ), а вне этого интервала равна нулю. Отсюда: ), а вне этого интервала равна нулю. Отсюда: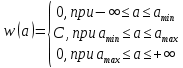 (2) (2)где: С – постоянная величина, которая из условия нормировки имеет значение равное 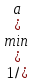 ; ;Функция распределения F(a) напрямую зависит от функции w(a) и определяется интегральным равенством (3): 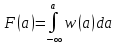 (3) (3)Зная значения функции w(a) на трёх интервалах, F(a) можно представить в виде: 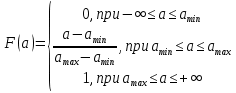 (4) (4)Таким образом, имея аналитические выражения (2) и (4) для функций F(a) и w(a), построим их графики (рис.2 и рис.3). 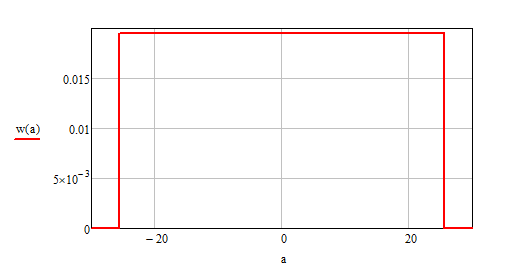 Рис.2 График функции плотности распределения вероятностей w(a) 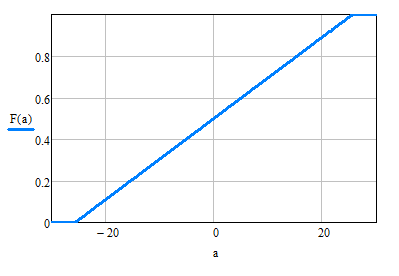 Рис.3 График функции распределения вероятностей F(a) 2) Для того, чтобы рассчитать математическое ожидание 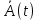 , воспользуемся интегральным выражением (5), имеющим вид: , воспользуемся интегральным выражением (5), имеющим вид: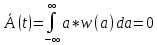 (5) (5)Математическое ожидание равно нулю. Это означает, что случайный процесс является центрированным. Дисперсию 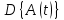 определим с помощью интегрального выражения (6): определим с помощью интегрального выражения (6):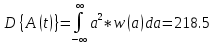 (6) (6)3) Поскольку сообщение A(t) является случайным процессом типа квазибелого шума, то спектральная плотность мощности 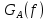 постоянна на частотном интервале ( постоянна на частотном интервале ( ) и равна нулю вне этого интервала. Обозначит через ) и равна нулю вне этого интервала. Обозначит через  значение функции значение функции 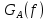 на интервале ( на интервале (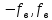 ). ).Односторонняя спектральная плотность, которая задаётся равенством 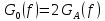 равномерна на частотном интервале ( равномерна на частотном интервале (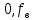 ) и равна нулю вне этого интервала. ) и равна нулю вне этого интервала.Поскольку мощность 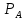 случайного процесса A(t) равна площади прямоугольника с основанием случайного процесса A(t) равна площади прямоугольника с основанием 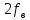 и высотой и высотой 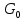 , то: , то: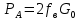 (7) (7)Эта мощность так же равна дисперсии 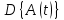 , которая была получена в выражении (6), то есть: , которая была получена в выражении (6), то есть: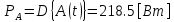 (8) (8)Отсюда следует: 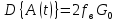 (7) (7)Таким образом, выполнив преобразования равенства (8), получим, что постоянная величина 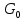 равняется: равняется: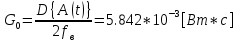 (9) (9)Зная величину 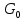 , можно записать аналитическое выражение (10) для спектральной плотности мощности , можно записать аналитическое выражение (10) для спектральной плотности мощности 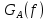 : :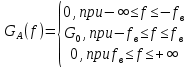 (9) (9)На основе аналитического выражения (10) построим график спектральной плотности мощности 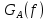 (рис.4). (рис.4).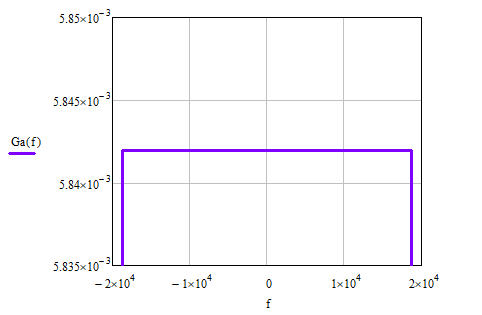 Рис.4 График спектральной плотности мощности 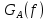 4) Корреляционную функцию 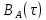 найдём с помощью теоремы Винера-Хинчина, которая утверждает, что спектральная плотность мощности случайного процесса есть преобразование Фурье соответствующей автокорреляционной функции. Поэтому для нахождения корреляционной функции воспользуемся выражением (11): найдём с помощью теоремы Винера-Хинчина, которая утверждает, что спектральная плотность мощности случайного процесса есть преобразование Фурье соответствующей автокорреляционной функции. Поэтому для нахождения корреляционной функции воспользуемся выражением (11):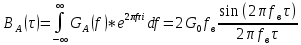 (11) (11)Поскольку 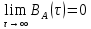 , то случайный процесс A(t) является эргодическим, то есть такой, у которого статистика, полученная по ансамблю реализаций, совпадает со статистикой одной из реализаций. , то случайный процесс A(t) является эргодическим, то есть такой, у которого статистика, полученная по ансамблю реализаций, совпадает со статистикой одной из реализаций.На основе выражения (10) изобразим график корреляционной функции  (рис.5). (рис.5).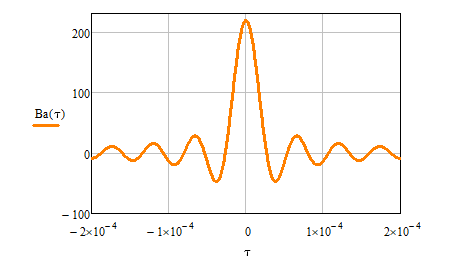 Рис. 5 График корреляционной функции 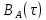 сообщения A(t) сообщения A(t) |

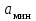 ,
, 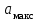 (В)
(В)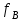
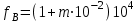 (Гц)
(Гц)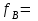 1,87 ∙10 4 (Гц)
1,87 ∙10 4 (Гц)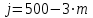
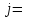 239
239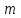
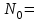 1,85∙10-7
1,85∙10-7 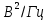
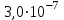
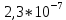
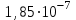
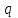 –
– 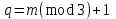
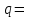 1
1