Модулятор
В состав модулятора структурной схемы цифровой системы связи (ЦСС), рис. 1, между блоками ФМС и перемножителями входят сглаживающие формирующие фильтры СФФ, необходимые для оптимизации ЦСС в отношении межсимвольной помехи, а также инвертор и сумматор, на выходе которого получаем сигнал заданного вида модуляции.
Сглаживающий формирующий фильтр
Требуется:
1) Изобразить структурную схему модулятора в составе ЦСС;
2) написать аналитические выражения для сигнала 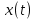 со «спектром приподнятого косинуса» (импульса Найквиста) и его спектральной плотности со «спектром приподнятого косинуса» (импульса Найквиста) и его спектральной плотности 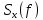 для значений коэффициента сглаживания для значений коэффициента сглаживания 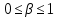 . Изобразить графики сигналов . Изобразить графики сигналов 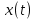 и соответствующие спектральные плотности при и соответствующие спектральные плотности при 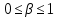 ; ;
3) На одном рисунке изобразить графики спектральных плотностей 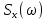 и и 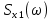 сигналов сигналов 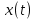 и и 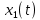 , где , где 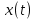 – импульс Найквиста при коэффициенте сглаживания – импульс Найквиста при коэффициенте сглаживания 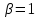 ; 1 ; 1 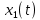 – импульс со спектральной плотностью – импульс со спектральной плотностью 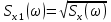 ; ;
4) На одном рисунке изобразить графики импульсов 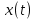 и и 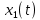 ; ;
5) Написать аналитические выражения для случайных процессов 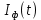 и и 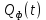 ; ;
6) Написать аналитические выражения для корреляционных функций и спектральных плотностей мощности случайных процессов 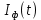 и и 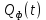 и построить графики этих функций. и построить графики этих функций.
1) Структурная схема модулятора изображена на рис.21.
             
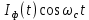
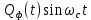
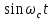
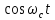
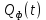
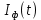
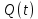
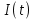
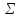

-1
СФФ2
СФФ1
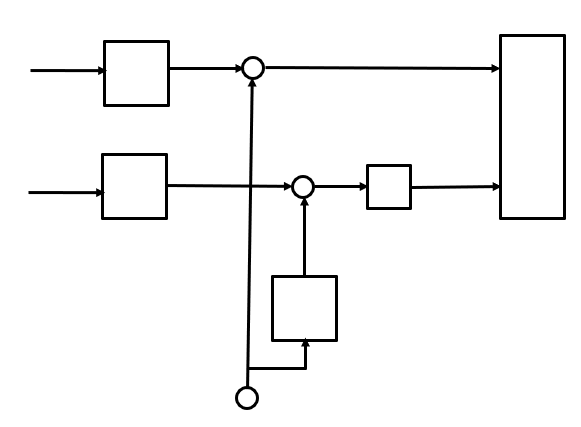
Рис. 21 Структурная схема модулятора
2) Использование импульсов Найквиста для транспортировки информационных символов (ИС) по каналу связи позволяет построить цифровую систему связи (ЦСС), в которой не возникают межканальная и межсимвольная помехи. Оптимизируется приём в условиях флуктационной помехи типа белого шума.
Импульсы Найквиста и их спектральные плотности характеризуются аналитическими выражениями (30) и (31):
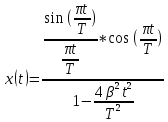 (30) (30)
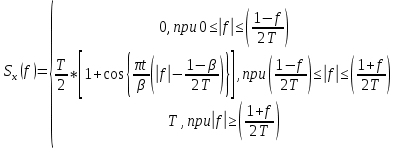 (31) (31)
где:
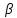 -коэффициент сглаживания, который может принимать значения на интервале -коэффициент сглаживания, который может принимать значения на интервале 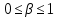 ; ;
Графики для выражений (30) и (31) показаны ниже на рис.22 и рис.23.
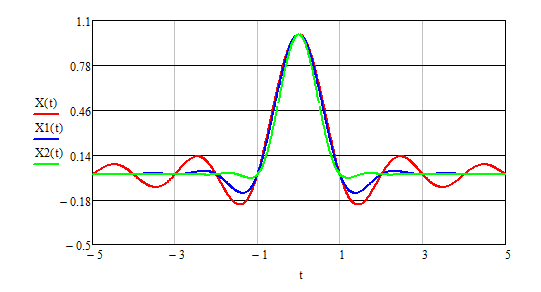
Рис. 22 График сигнала x(t) со спектром «приподнятого косинуса» (импульса Найквиста) при 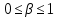
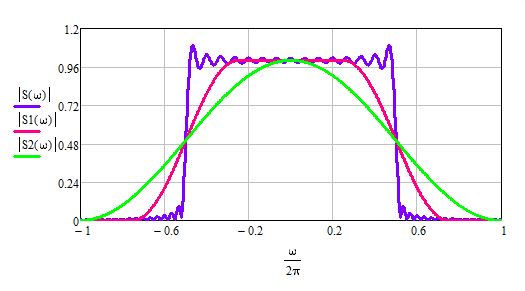
Рис. 23 Спектральные плотности для сигнала x(t) при 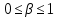
3) На рис.24 изображены графики спектральных плотностей 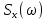 и и 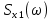 сигналов сигналов 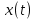 и и 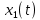 , где , где 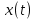 – импульс Найквиста при коэффициенте сглаживания – импульс Найквиста при коэффициенте сглаживания 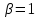 ; ; 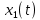 - импульс со спектральной плотностью - импульс со спектральной плотностью 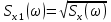 . .
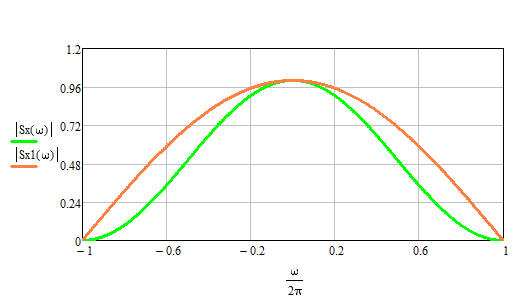
Рис. 24 График спектральных плотностей 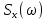 и и 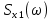
4) На рис.25 изображены сигналы 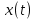 и и 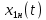 , где , где 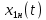 – нормированный импульс – нормированный импульс 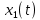 . Так как амплитуда сигнала . Так как амплитуда сигнала 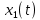 на два порядка больше амплитуды импульса Найквиста на два порядка больше амплитуды импульса Найквиста 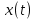 , то необходимо перейти к нормированному импульсу , то необходимо перейти к нормированному импульсу 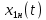 , который записывается в виде: , который записывается в виде:
 (32) (32)
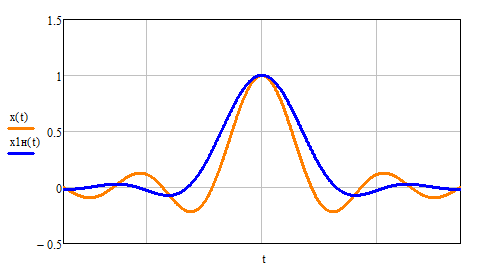
Рис. 25 Графики сигналов 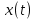 и и 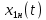
5) Прямоугольные импульсы 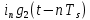 (где (где 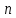 – номер символьного интервала) после прохождения через СФФ преобразуются в импульсы – номер символьного интервала) после прохождения через СФФ преобразуются в импульсы 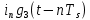 . .
Форма этих импульсов 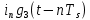 соответствует форме усеченного нормированного импульса соответствует форме усеченного нормированного импульса 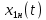 . Но эти импульсы сдвинуты вправо на время . Но эти импульсы сдвинуты вправо на время 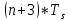 относительно импульса относительно импульса 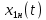 , т. е: , т. е:
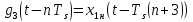 (33) (33)
При 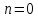 получаем: получаем:
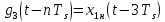 (34) (34)
Импульс 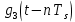 подаётся на согласованные фильтры (СФ1 и СФ2) вместе с импульсами подаётся на согласованные фильтры (СФ1 и СФ2) вместе с импульсами 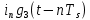 и и 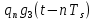 , в результате чего на выходе сглаживающего фильтра формируются соответствующие импульсы Найквиста, которые обеспечивают отсутствие межсимвольной помехи при взятии отсчётов главных максимумов этих импульсов. , в результате чего на выходе сглаживающего фильтра формируются соответствующие импульсы Найквиста, которые обеспечивают отсутствие межсимвольной помехи при взятии отсчётов главных максимумов этих импульсов.
В результате, на выход сумматора поступают случайные величины 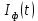 и и 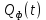 , которые задаются следующими формулами: , которые задаются следующими формулами:
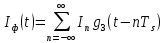 (35) (35)
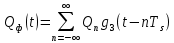 (36) (36)
6) Корреляционные функции 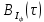 и и 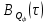 равны друг другу, поскольку ансамбли реализаций равны друг другу, поскольку ансамбли реализаций 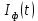 и и 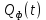 имеют одинаковые статистические характеристики. Таким образом, аналитические выражения для корреляционных функций имеют одинаковые статистические характеристики. Таким образом, аналитические выражения для корреляционных функций 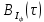 и и 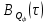 записываются в виде: записываются в виде:
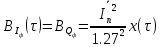 (37) (37)
где:
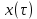 – импульс Найквиста при значении коэффициента сглаживания – импульс Найквиста при значении коэффициента сглаживания 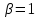 ; ;
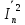 - величина равная - величина равная 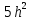 в соответствии с сигнальным созвездием КАМ-16; в соответствии с сигнальным созвездием КАМ-16;
На основе теоремы Винера-Хинчина можно рассчитать спектральные плотности мощности 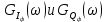 . Они так же будут равны. Отсюда получаем выражение (38): . Они так же будут равны. Отсюда получаем выражение (38):
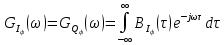 (38) (38)
Преобразуем выражение (38). Будем иметь:
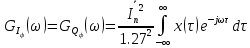 (39) (39)
На основании выражения (31) по итогу получаем следующую систему:
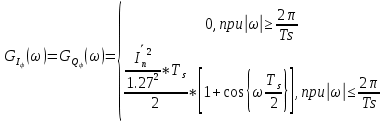 (40) (40)
Графики для выражений (38) и (40) представлены ниже на рис.26, рис.27, рис.28 и рис.29.
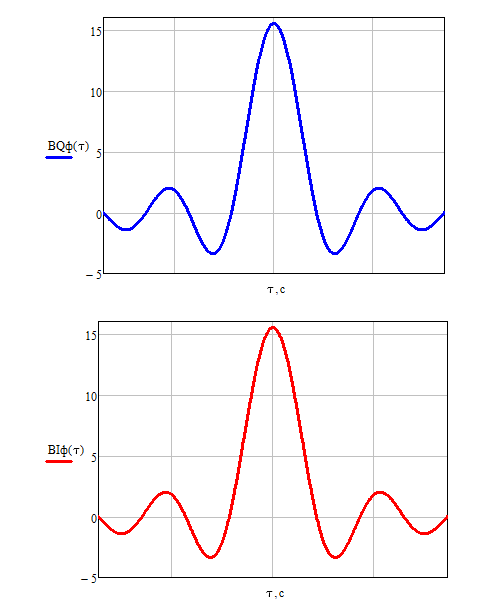
Рис. 26 Графики корреляционных функций 
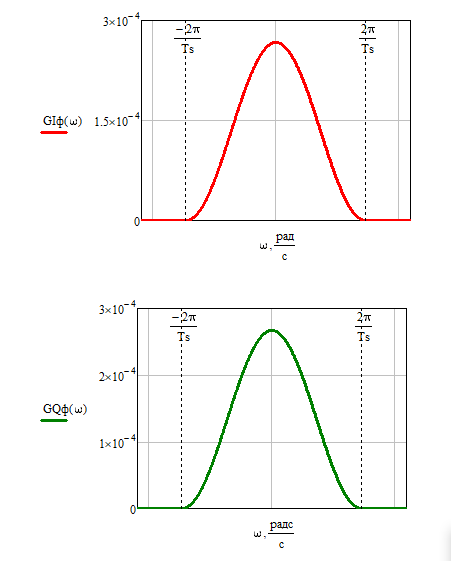
Рис.27 Графики спектральных плотностей мощности 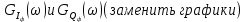
Блоки перемножителей, инвертор, сумматор
Требуется:
1) Написать аналитические выражения для корреляционных функций 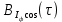 и и 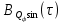 случайных сигналов случайных сигналов 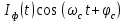 и и 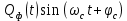 на выходах перемножителей, где на выходах перемножителей, где 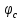 – случайная фаза с равномерной плотностью вероятности на интервале 0…2. Случайная фаза – случайная фаза с равномерной плотностью вероятности на интервале 0…2. Случайная фаза 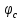 не зависит от случайных процессов не зависит от случайных процессов 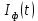 и и 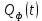 ; ;
2) Написать аналитические выражения для корреляционных функций 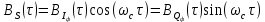 и для спектральной плотности мощности и для спектральной плотности мощности 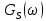 сигнала сигнала 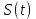 на выходе сумматора для заданного вида модуляции. Построить графики этих функций. на выходе сумматора для заданного вида модуляции. Построить графики этих функций.
1) При прохождении сигналов 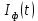 и и 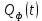 через перемножители, инвертор и дальнейшем их поступлении на вход сумматора формируется сигнал через перемножители, инвертор и дальнейшем их поступлении на вход сумматора формируется сигнал 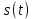 , выражение для которого задаётся в следующей форме: , выражение для которого задаётся в следующей форме:
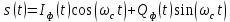 (41) (41)
Множители 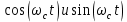 обеспечивают ортогональность сигналов обеспечивают ортогональность сигналов 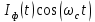 и и 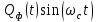 . Эти сигналы передаются одновременно, в одной и той же полосе частот по одной линии связи. Таким образом, обеспечивается линейная независимость сигналов. На приёмном конце канала возможно разделение этих двух сигналов. . Эти сигналы передаются одновременно, в одной и той же полосе частот по одной линии связи. Таким образом, обеспечивается линейная независимость сигналов. На приёмном конце канала возможно разделение этих двух сигналов.
При задании случайных процессов на выходе перемножителей, детерминированные функции 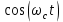 и и 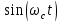 , необходимо расширить до случайных функций , необходимо расширить до случайных функций 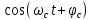 и и 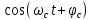 введением в аргумент детерминированных функций случайной фазы введением в аргумент детерминированных функций случайной фазы 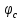 . Фаза . Фаза 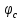 , в свою очередь, не зависит от величин , в свою очередь, не зависит от величин 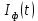 и и 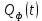 . .
Функция плотности вероятности 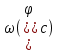 фазы фазы 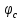 является равномерной. Задаётся выражение для функции является равномерной. Задаётся выражение для функции 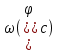 в виде: в виде:
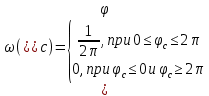 (42) (42)
Таким образом, вместо сигнала (41) на выходе сумматора получим случайный процесс в следующем виде:
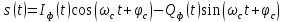 (43) (43)
Как итог, выражение (43) помогает определить корреляционную функции. случайного сигнала КАМ-16 на выходе сумматора.
На выходе верхнего перемножителя формируется сигнал:
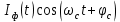 (44) (44)
На выходе нижнего перемножителя формируется сигнал:
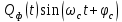 (45) (45)
Корреляционные функции 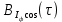 и и 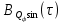 запишем в следующей форме: запишем в следующей форме:
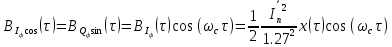 (46) (46)
где:
 - импульс Найквиста при значении коэффициента сглаживания - импульс Найквиста при значении коэффициента сглаживания  ; ;
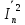 - величина равная - величина равная 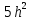 в соответствии с сигнальным созвездием КАМ-16; в соответствии с сигнальным созвездием КАМ-16;
2) Аналитические выражения для корреляционных функций 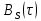 имеет вид: имеет вид:
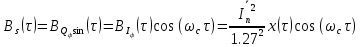 (47) (47)
где:
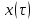 - импульс Найквиста при значении коэффициента сглаживания - импульс Найквиста при значении коэффициента сглаживания 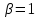 ; ;
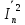 - величина равная - величина равная 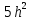 в соответствии с сигнальным созвездием КАМ-16; в соответствии с сигнальным созвездием КАМ-16;
Спектральную плотность мощности найдём с помощью теоремы Винера-Хинчина. Она определяется через преобразование Фурье корреляционной функцией 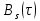 . Получим: . Получим:
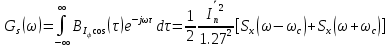 (48) (48)
Аналитические выражения для функций 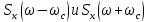 представлены ниже: представлены ниже:
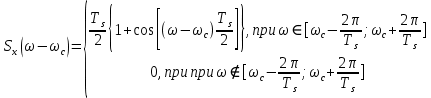 (49) (49)
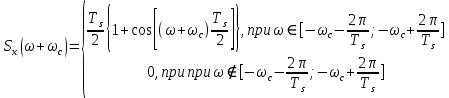 (50) (50)
Графики функций для выражений (47) и (48) изображены на рис.28 и рис.29.
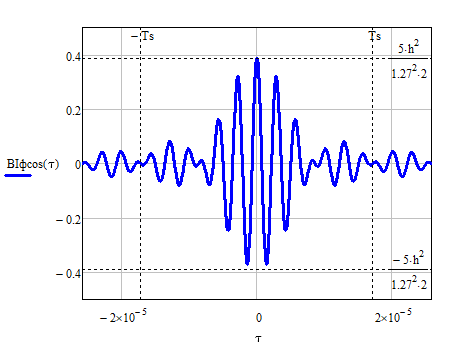
Рис. 28 График корреляционной функции 
|
 Скачать 1.25 Mb.
Скачать 1.25 Mb.