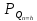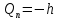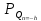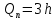Курсовая работа по дисциплине ТЭС. Курсовая ТЭС. Расчёт основных характеристик цифровой системы связи с использованием квадратурной модуляции
 Скачать 1.25 Mb. Скачать 1.25 Mb.
|
ДемодуляторТребуется: 1) Изобразить структурную схему когерентного демодулятора, оптимального по критерию максимального правдоподобия для заданного сигнала квадратурной модуляции; 2) Написать алгоритмы работы решающих устройств РУ1 и РУ2 в составе когерентного демодулятора; 3) Определить вероятности ошибок на выходах РУ1 и РУ2: а) В случае КАМ-16 при значениях символов 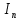 и и 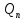 , равных , равных 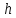 , , 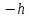 , , 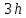 , , 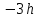 , когда , когда 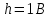 ; ; б) В случае КФМ-4 при значениях символов 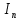 и и 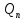 , равных , равных 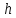 и и 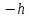 , когда , когда 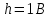 ; ;4) На четырех символьных интервалах длительностью 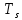 нарисовать сигналы на выходах РУ1 и РУ2 демодулятора, соответствующие сигналам на выходе блока ФМС, которые поступают на два входа преобразователя параллельного кода в последовательный код. Под двумя построенными графиками, используя сигнальное созвездие для заданного вида модуляции, изобразить график сигнала на выходе преобразователя кода в виде соответствующей последовательности прямоугольных импульсов на входе блока ФМС длительностью нарисовать сигналы на выходах РУ1 и РУ2 демодулятора, соответствующие сигналам на выходе блока ФМС, которые поступают на два входа преобразователя параллельного кода в последовательный код. Под двумя построенными графиками, используя сигнальное созвездие для заданного вида модуляции, изобразить график сигнала на выходе преобразователя кода в виде соответствующей последовательности прямоугольных импульсов на входе блока ФМС длительностью 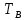 ; ; 5) Определить вероятности ошибок 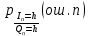 ; ; 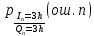 ; ; 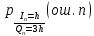 на выходе преобразователя параллельного кода в последовательный код, где 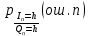 – обозначение вероятности ошибочного приема, если – обозначение вероятности ошибочного приема, если 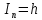 , , 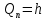 ; ;Определить среднюю вероятность ошибки на выходе преобразователя при условии, что имеют место равенства: 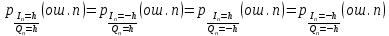 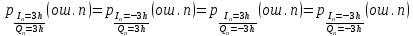 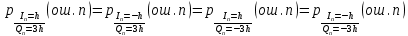 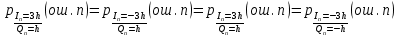 Структурная схема когерентного демодулятора оптимального по критерию максимального правдоподобия для заданного сигнала квадратурной модуляции изображена на рис.30. 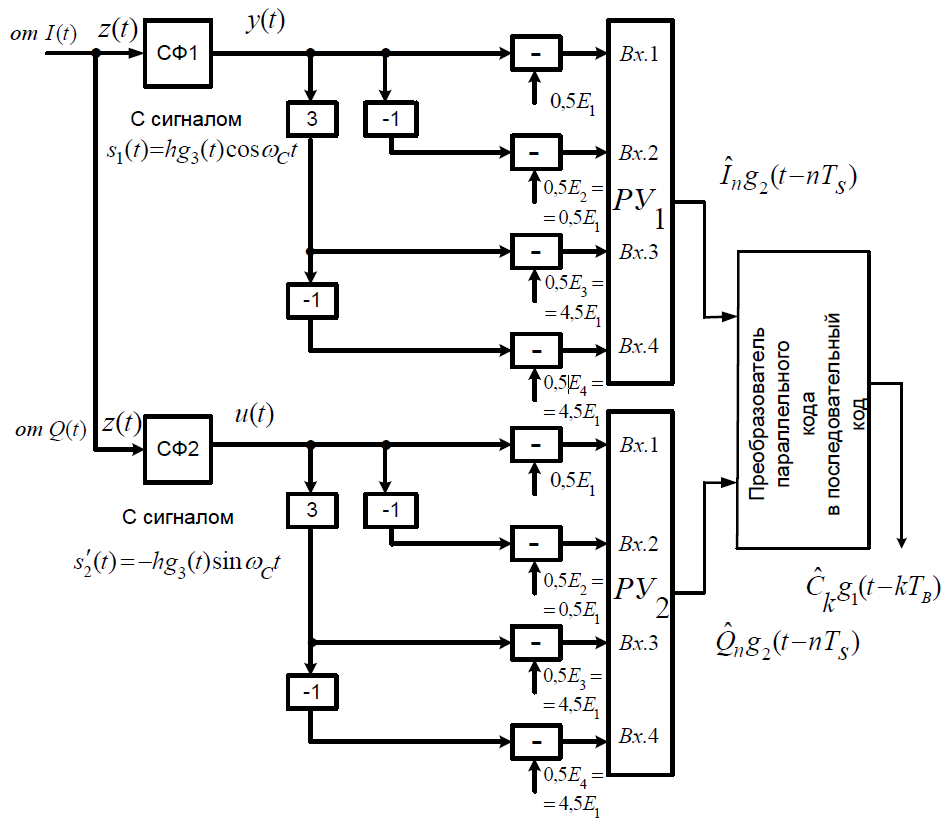 Рис. 30 Структурная схема когерентного демодулятора оптимального по критерию максимального правдоподобия для заданного сигнала квадратурной модуляции Алгоритмы работы решающих устройств РУ1 и РУ2 основаны на осуществлении оценки модулирующих символов 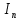 и и 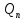 . В момент окончания символьного интервала . В момент окончания символьного интервала 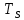 решающее устройство сравнивает 4 входных напряжения и выбирает из них максимальное. Таким образом, осуществляется процесс решения. Входные напряжения в свою очередь определяются следующими выражениями ((57), (58), (59) и (60) – для РУ1; (61), (62), (63) и (64) – для РУ2): решающее устройство сравнивает 4 входных напряжения и выбирает из них максимальное. Таким образом, осуществляется процесс решения. Входные напряжения в свою очередь определяются следующими выражениями ((57), (58), (59) и (60) – для РУ1; (61), (62), (63) и (64) – для РУ2):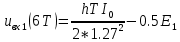 (57) (57)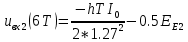 (58) (58)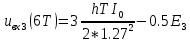 (59) (59)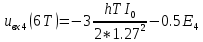 (60) (60)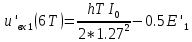 (61) (61)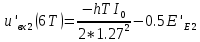 (62) (62)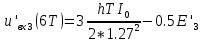 (63) (63)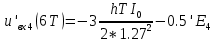 (64) (64)где: 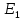 , , 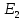 , , 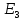 и и 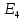 – энергии сигналов – энергии сигналов 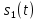 , , 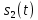 , , 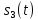 и и 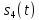 равные, соответственно: равные, соответственно: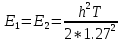 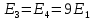 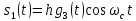 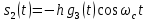 ; ;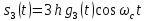 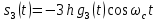 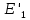 , , 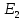 , , 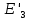 и и 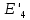 – энергии сигналов – энергии сигналов 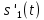 , , 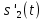 , , 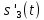 и и 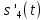 равные, соответственно: равные, соответственно: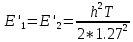 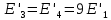 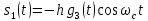 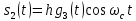 ; ;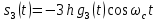 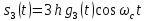 По итогу имеем выражение (65): 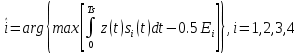 (65) (65)где: 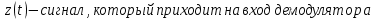 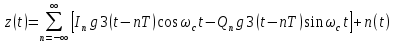 В момент окончания каждого символьного интервала длительностью Ts решающее устройство РУ1 (и РУ2) определяет номер входа 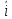 , на котором напряжение максимально, и формирует соответствующий дибит в параллельном формате: , на котором напряжение максимально, и формирует соответствующий дибит в параллельном формате: «00» при 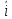 = 1, «10» при = 1, «10» при 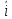 = 2, «01» при = 2, «01» при 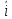 = 3, «11» при = 3, «11» при 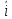 = 4. = 4.Для нахождения вероятностей ошибок на выходах решающих устройств РУ1 и РУ2 следует для начала рассчитать энергию 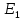 , которая будет равна из выражения (66): , которая будет равна из выражения (66):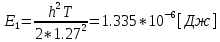 (66) (66)Далее определим ошибки 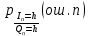 , , 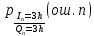 , , 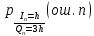 по формулам: по формулам: 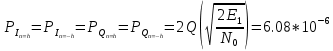 (67) (67)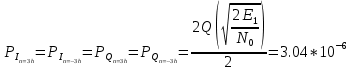 (68) (68)Таблица 3 Результат ошибки в решающем устройстве РУ1
Таблица 4 Результат ошибки в решающем устройстве РУ2
 Рис. 31 Сигналы на выходах РУ1 и РУ2 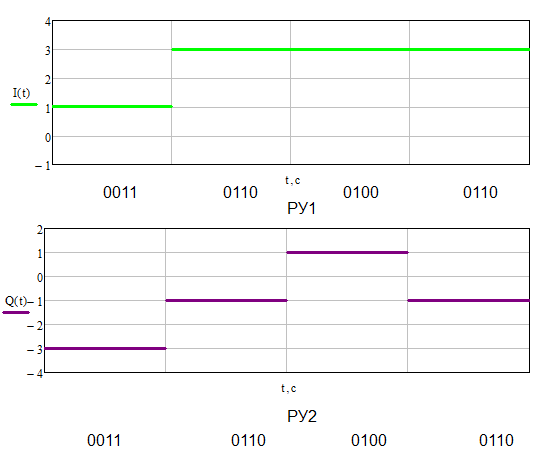 Сигналы на входах РУ1 и РУ2 представлены на рис.31: Сигналы на входах РУ1 и РУ2 представлены на рис.31:    Cигнал на выходе преобразователя кода примет вид (рис.32):    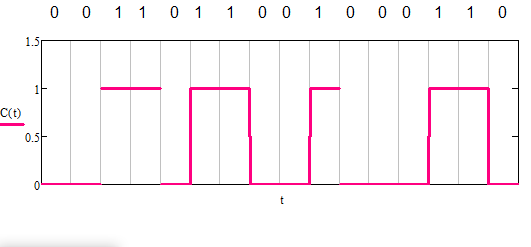 Рис. 32 Сигнал на выходе преобразователя кода 5) Определим вероятности ошибок на выходе преобразователя кода в последовательный код: 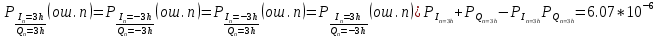 (69) (69)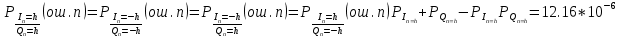 (70) (70)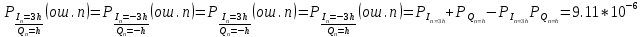 (71) (71)В результате, средняя величина вероятности ошибки на выходе преобразователя будет равна: 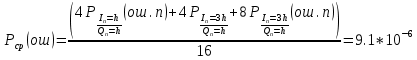 (72) (72) |

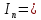 h
h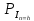
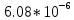
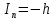
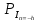
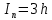
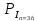
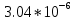
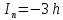
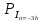
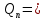 h
h