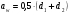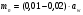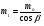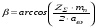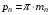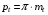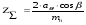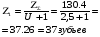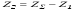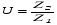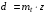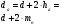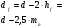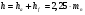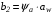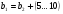Детали машин. Расчет основных характеристик редуктора. 1 Определяем мощность на исполнительном механизме
 Скачать 470.07 Kb. Скачать 470.07 Kb.
|
: 0,978).Суммарное число зубьев определим по формуле:  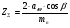 ; ; 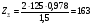 Разобьем суммарное число зубьев на число зубьев на шестерне и колесе. Минимальное число зубьев шестерен обычно ограничивается условием неподрезания зубьев у основания. Для некорригированных передач Zmin = 17, для корригированных Zmin = 12…14 и меньше. Число зубьев на шестерне: 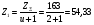 Число зубьев на колесе: 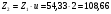 Округляем числа зубьев до целых значений 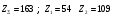 зубьев зубьевУточним угол β: 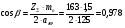 . .Т.е.угол 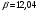 2.8 Определение диаметров колес. Диаметры делительных окружностей определяют по формуле:  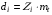 В нашем случае: 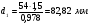 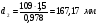 Проверка: 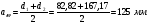 Параметры исходного контура цилиндрических зубчатых колес стандартизованы (ГОСТ 13755-81); угол профиля α = 20º; высота головки зуба hа = mn; высота ножки зуба hf = 1,25 mn; высота зуба h = hа + hf = 2,25 mn. Диаметры вершин зубчатых колес определим по формулам: 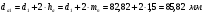 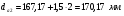 Диаметры впадин зубчатых колес найдем по формулам: 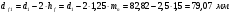 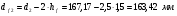 2.9 Выбор степени точности зубчатых колес Степень точности зубчатой передачи назначают в зависимости от окружной скорости. Окружная скорость колес по делительным окружностям находится по формуле: 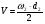 , ,где 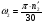 – угловая скорость зубчатого колеса – угловая скорость зубчатого колеса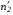 - уточненное число оборотов на колесе. - уточненное число оборотов на колесе.Итак, 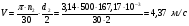 Степени точности зубчатых передач приведены в таблице 3. Таблица 3
Назначаем 8-ю степень точности зубчатого зацепления. Основные геометрические параметры приведены в таблице 4 Таблица 4
Продолжение таблицы 4
2.10 Определение числовых значения сил, действующих в зацеплении. В зацеплении действуют окружная сила Ft,радиальная сила Fr, и осевая сила Fa. 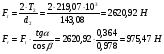 ( для стандартного угла 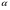 = =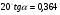 ) )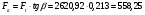 Н Н
3.1 Предварительный (проектный) расчёт вала. 3.1.1Выбор материала. Для валов редуктора общего назначения применяют углеродистые стали Ст3, Ст4, Ст5, 25, 30, 40 и 45 без термообработки. Валы, к которым предъявляются требования по несущей способности и долговечности, изготавливают из улучшенных среднеуглеродистых или легированных сталей 35, 40, 45, 40Х, 40ХН и др. Ответственные тяжелонагруженные валы изготавливают из легированных сталей 40ХН, 40ХН2МА, 30ХГТ и др. В данном случае для вала редуктора назначаем улучшенную сталь 30. σТ = 300 МПа; σ -1Р = 200 МПа; σ -1 = 250 МПа; σВ = 600 МПа; τ -1 = 140 МПа; НВ = 179; Е = 2∙10 11 МПа; μ = 0,27. 3.1.2 Определение минимального диаметра тихоходного вала. Так как конструкция вала (места приложения нагрузки, расположение опор и т.п.) на данном этапе неизвестна, то предварительно определяем диаметр вала из расчёта только на кручение по формуле: 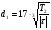 Т 2 – максимальный крутящий момент, передаваемый валом, |τ| - допускаемое напряжение, для сталей |τ| = 12 ÷ 35 МПа; 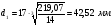 Диаметр вала (стандартный ряд чисел): 10; 10,5; 11; 11,5; 12; 13; 14; 15; 16; 17; 18; 19; 20; 21; 22; 24; 25; 26; 28; 30; 32; 34; 36; 38; 40; 42; 45; 48; 50; 52; 55; 60; 63; 65; 70; 75; 80; 85; 90; 95; 100; 105; 110; 120; 125; 130; 140; 150; 160 и т.д. Приравниваем полученное (расчётное) значение к стандартному. Из стандартного ряда чисел подходит – 42 (мм). d 1 = 42 (мм). 3.1.3 Определение размеров вала. 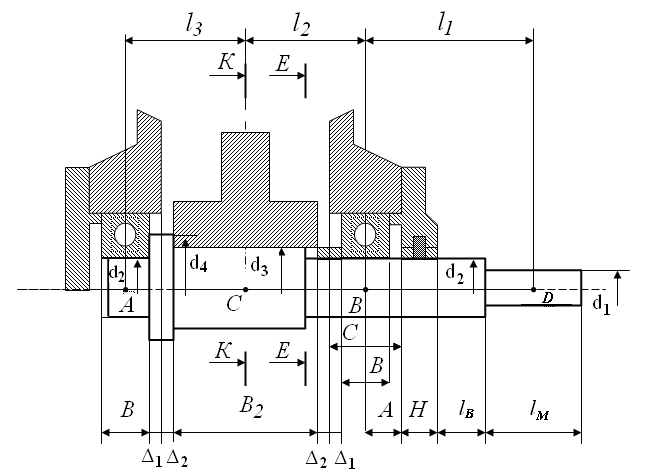 Рисунок 1. Конструкция тихоходного вала редуктора. Остальные диаметры вала назначаем по конструктивным соображениям с учётом удобства посадки на вал зубчатых колёс, подшипников качения и других деталей и необходимости их фиксации на валу в осевом направлении. Диаметр вала в месте посадки правого подшипника должен быть равен внутреннему диаметру ближайшего по типоразмеру подшипника; при этом высота заплечика должна быть больше фаски на ступице муфты. Исходя из этого выражения: d 2 = d 1 + 3…5 (мм); d 2 =42 + 3 = 45 (мм). Выбираем по таблице ГОСТ 8338–75 подшипник лёгкой серии с габаритными размерами D= 85 (мм), В = 19 (мм). Запомним, что подшипники в диапазоне внутренних диаметров 3…10 мм стандартизованы через 1 мм, до 20 мм – через 2…3 мм, до 110 мм – через 5 мм, до 200 мм – через10 мм, до 500 мм через 20 мм и .т.д. Поэтому диаметр d2, т.е. вала под подшипником округляется до стандартного размера внутреннего диаметра подшипника. Для унификации подшипники обеих опор принимаем одинаковыми. Диаметр вала в месте установки уплотнения можно принять также равным d 2 = 45 (мм). Диаметр вала в месте посадки зубчатого колеса рассчитываем по формуле: d 3 = d 2 + 3…5 (мм), d 3 = 45 + 5 = 50 (мм). Округляем полученное значение до ближайшего стандартного размера из ряда значений. d 3 = 50 (мм). Диаметр буртика вала (заплечика) рассчитываем по формуле: d 4 = d 3 +10…15 (мм), d 4 = 50 + 10 = 60 (мм). Округляем полученное значение до ближайшего стандартного из ряда значений. d 4 = 60 (мм). Между торцом муфты и крышкой подшипника рекомендуется оставлять зазор, принимаем ℓ В = 10 (мм). H = 10 (мм). Учитывая возможную неточность положения стенки корпуса, подшипники отодвигают от края стенки на расстояние Δ 1 = 3 ÷ 6 (мм), выбираем Δ 1 = 5 (мм). Расстояние между внутренними стенками корпуса и зубчатым колесом редуктора можно определить из выражения: Δ 2 ≥ 1,15∙(0,025∙ аw + 1), но Δ 2 должно быть не менее 8 (мм), Δ 2 = 1,15∙(0,025∙ 100 + 1) = 4,03 (мм), принимаем Δ 2 = 8 (мм). Длина ℓ П.М.зависит от зубчатой муфты, по d 1= 42 (мм) выбираем муфту: тип 2, исполнение 2; D = 170 (мм);ℓ = 169 (мм); ℓ П.М. = 38 (мм). Длину вала на участке ВD рассчитываем по следующей формуле: ℓ 1 = ℓ П.М. / 2 + Н + ℓВ + А, А = С – В / 2 – 5 (мм), С = 2,5∙d 1(болта) + δ, δ – толщина стенки, δ = 6…10 (мм), dф=(0,03 аw +12) мм d 1(болта) = 0,75∙d фунд., d фунд. = 0,03∙aW + 12 (мм); d фунд. = 0,03∙125 + 12 = 16 (мм), d 1(болта) = 0,75∙16 = 12 (мм), Округляем полученное значение до ближайшего стандартного из ряда значений. d 1(болта)= 12 (мм), С = 2,5∙12 + 10 = 40 (мм), А = 40 – 19 / 2 – 5 = 25,5 (мм), ℓ 1= 84,5/ 2 + 10 + 10 + 25,5 = 87,75 (мм). Длину вала на участках АС и СВ рассчитываем по следующей формуле: ℓ 2 = ℓ3 = В / 2 + Δ 1 + Δ 2 + b 2 / 2; ℓ 2 = ℓ 3 = 19 / 2 + 5 + 8 + 50 / 2 = 47,5 (мм). Диаметры крепёжных болтов: d 1(болта) = 12 (мм). d 2(болта) = 0,5∙d фунд., d 2(болта) = 0,5∙16 = 8 (мм). Округляем полученное значение до ближайшего стандартного из ряда значений. d 2(болта) = 8 (мм). d 3(болта) = 0,3...0,4∙ d фунд., d 3(болта) = 0,3∙16 = 4,8 (мм). Округляем полученное значение до ближайшего стандартного из ряда значений. d 3(болта) = 4 (мм). 3.2 Проверочный (уточнённый) расчёт вала. 3.2.1 Составление расчётной схемы вала редуктора (Рис.2). XВ d 2 / 2 ℓ 3 ℓ 1 D B C XА y Fr Ft Fa YВ YА z x ℓ 2 Рис.2. Расчётная схема вала редуктора. 3.2.2 Построение эпюр моментов в вертикальной плоскости (Рис.3). 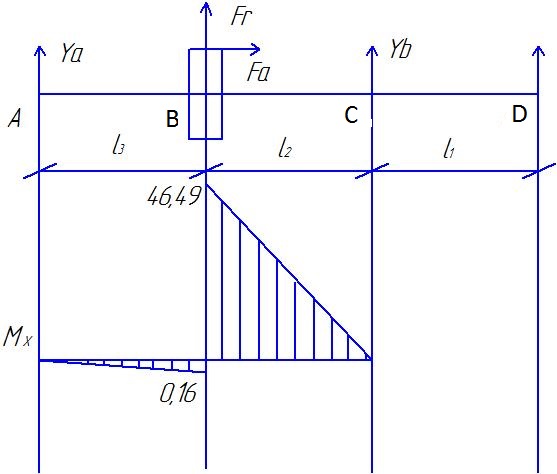 Рис.3. Схема действия сил (а), эпюра изгибающих моментов (б) в плоскости уАz. Определение опорных реакций от сил Fr и Fa: ∑МВ = 0; -YA∙(ℓ3 + ℓ 2 ) + Fr∙ℓ 2 -Fa∙(d2 / 2) = 0; YA = (Fr∙ℓ 3 - Fa∙(d2 / 2)) / (ℓ 2 + ℓ 3 ); YA = -3,4 (Н); ∑МА = 0; YВ∙(ℓ 2 + ℓ 3 ) - Fr∙ℓ 3 - Fa∙(d2 / 2) = 0; YB= 978,87 (H) Проверяем правильность определения реакций: ∑Y = 0; YA – Fr + YВ = 0; -3,4 – 975,47 + 978,87= 0. Реакции найдены правильно. Строим эпюру изгибающих моментов от сил Frи Fa М XC1 = Y A∙ℓ 3·10-3, М XC1 = -3,4·47,5·10-3= - 0,16 (Нм). М XC2 = Y B∙ℓ 2·10-3, М XC2 = 978,87·47,5·10-3 = 46,49 (Нм). 3.2.3 Построение эпюр в горизонтальной плоскости (Рис.4) | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||