Детали машин. Расчет основных характеристик редуктора. 1 Определяем мощность на исполнительном механизме
 Скачать 470.07 Kb. Скачать 470.07 Kb.
|
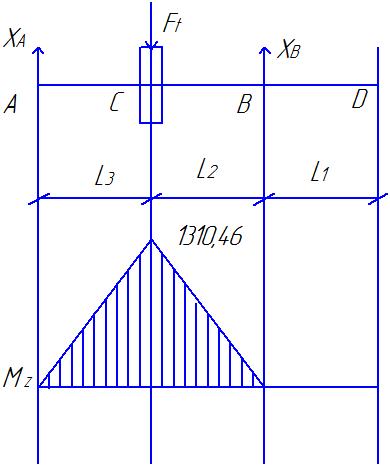 Рис.4. Схема действия сил (а) и эпюра изгибающих моментов (б) в плоскости xAz. Определяем опорные реакции от силы Ft ∑МВ = 0; -XA∙(ℓ 2 + ℓ 3 ) +Ft∙ℓ 2 = 0; XA = Ft∙ℓ 3 / (ℓ 2 + ℓ 3 ); XA = 2620,62·47,5/(47,5 + 47,5) = 1310,46 ∑МА = 0; XВ∙(ℓ 2 + ℓ 3 ) – Ftl3= 0; XВ = Ft∙ℓ 3 / (ℓ 2 + ℓ 3 ); XВ = 1310,46 Проверка правильности нахождения реакций: ∑X = 0; XВ+XА-Ft=0 1310,46+1310,46-2620,62=0 Реакции найдены правильно. Строим эпюру изгибающих моментов от силы Ft. МZC1 = XA∙ℓ 3·10-3, МZC1 = 1310,46·47,5·10-3 =62,24 (Н) МZC2 = X В∙ℓ 2·10-3, МZC2 = 1310,46·47,5·10-3 =62,24(Н) 3.2.4 Построение суммарной эпюры изгибающего момента от сил Fr, Ft и Fa (Рис.5). Ординаты суммарной эпюры изгибающих моментов от совместного действия сил (Рис.4) находим по формуле: МuC = (М2XC + М2ZC)1/2. 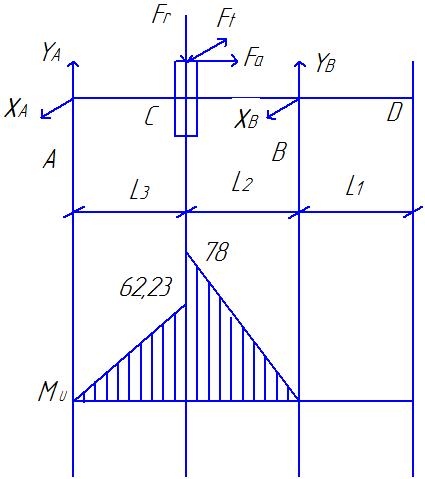 Рисунок 5. Эпюра изгибающего момента от совместного действия сил. Строим суммарную эпюру изгибающего момента. МuC1 = (М2XC1 + М2ZC)1/2, МuC1 = 62,23 (Нм). МuC2 = (М2XC2 + М2ZC)1/2, МuC2 = 78 (Нм). 3.2.5 Построение эпюры моментов от действия силы Q (Рис.6). 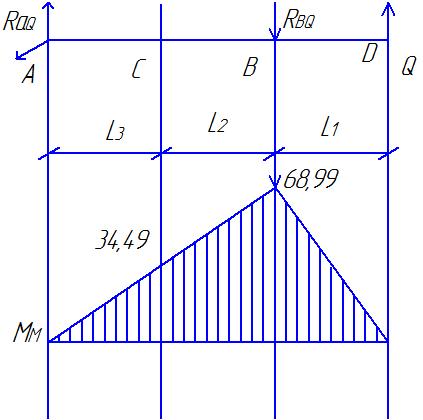 Рисунок 6. Схема действия силы Q и эпюра изгибающих моментов. В большинстве случаев муфты из-за несоосности соединяемых валов нагружают вал дополнительно поперечной силой Q. На тихоходном валу редуктора общего назначения должна быть предусмотрена расчётная консольная нагрузка, приложенная к середине выступающего конца вала и равная Q ≈0,3Ft. В нашем случае: Q ≈ 0,3∙ 2620,92=78,276 МПа Определяем опорные реакции от силы Q. ∑М В = 0; -RAQ∙(ℓ 2 + ℓ 3 ) + Q∙ℓ 1 = 0; RAQ = Q∙ℓ 1 / (ℓ 2 + ℓ 3 ), RAQ = 726,27 (Н). ∑М А = 0; -R ВQ∙(ℓ 2 + ℓ 3 ) + Q∙(ℓ 1 + ℓ 2 + ℓ 3) = 0; R ВQ = Q∙(ℓ 1 + ℓ 2 + ℓ 3) / (ℓ 2 + ℓ 3 ), R ВQ = 1512,54 (Н). Проверяем правильность определения реакций: RAQ - R ВQ + Q = 0, 726,27-1512,54+786,276 = 0. Реакции найдены правильно. Строим эпюру изгибающего момента от силы Q. М МВ = R АQ∙(ℓ 2 + ℓ 3 )·10-3, М МВ = 68,99 (Нм). М МС = ММВ / 2 М МС = 68,99/ 2 = 34,49 (Нм). 3.2.6 Построение суммарной эпюры изгибающих моментов от действия всех сил. Ординаты суммарной эпюры изгибающих моментов от совместного действия всех сил находим по формуле: М ∑ = Мu + М М. Строим суммарную эпюру изгибающих моментов от действия всех сил (Рис.7). М ∑С1 = МuС1 + М МС = 96,72 (Нм). М ∑С2 = МuС2 + М МС = 112,49 (Нм). МΣВ = МuВ + ММВ = 68,99 (Нм). 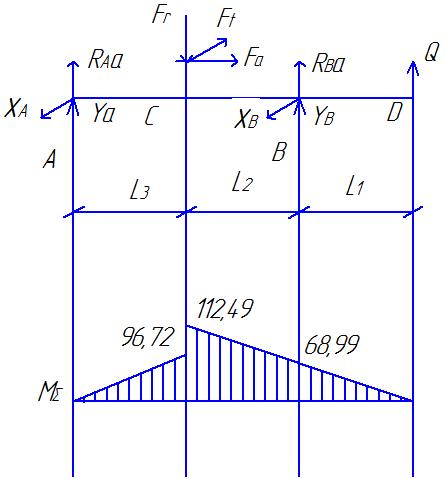 Рисунок 7. Суммарная эпюра изгибающих моментов. 3.2.7 Построение эпюры крутящих моментов. 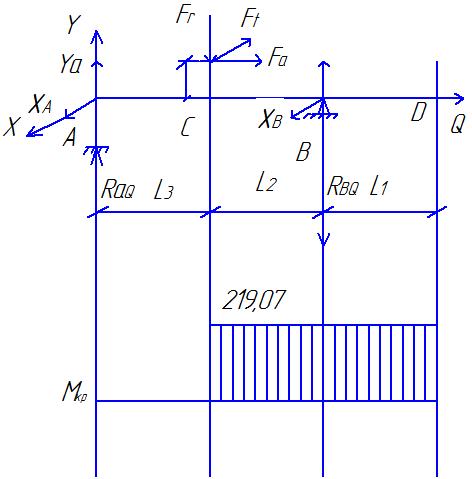 Рисунок 8. Эпюра крутящих моментов. 3.2.8 Определение опасных сечений вала. Намечаем опасные сечения вала, которые подлежат проверке на предел выносливости: сечение С (шпоночный паз и действует Mmax) и Е (канавка с галтелью). При расчёте учитываем напряжения от совместного действия изгибающих и крутящих моментов. Действующие на вал нормальные и поперечные силы не учитываем, так как они вызывают в сечениях вала напряжения, значительно меньшие, чем от изгибающих и крутящих моментов. 3.2.9 Проверка прочности сечения в точке С (Рис.1, сечение К – К). В сечении К – К действует изгибающий момент М и = 112,49 (Нм) и крутящий момент М к = 219,07 (Нм). Напряжения изгиба изменяются по симметричному циклу, напряжение кручения – по отнулевому (пульсирующему) циклу. σ а = σ и = М и / W и. нетто, τ а = τm = τ к / 2 = М к / 2∙ W к. нетто, W и. нетто – момент сопротивления изгибу сечения, ослабленного шпоночной канавкой, W к. нетто – момент сопротивления кручения сечения, ослабленного шпоночной канавкой. В нашем случае диаметр вала равен 50 мм (d 3 = 50 мм), тогда: b = 14 (мм), h = 9 (мм), b и t 1 – ширина и высота шпонки. W и. нетто = (π∙d 3 / 32) – (b∙t 1∙(d – t 1) 2 / 2∙d), W к. нетто = (π∙d 3 / 16) – (b∙t 1∙(d – t 1) 2 / 2∙d), W и. нетто=10,65 (см 3), W к. нетто = 22,9 (см 3). σ а = σ и = 112,49 / 10,65 = 10,56 (МПа). σm = 0. τ а = τm = 219,07 / (2∙22,9) = 4,78 (МПа). Коэффициенты запаса прочности по нормальным и касательным напряжениям вычисляем по формулам: n σ = σ -1 / ((к σ / ε σ∙β)∙σа + ψ σ∙σm), n τ = τ -1 / ((к τ / ε τ∙β)∙τа + ψ τ∙τm); σ -1 – предел выносливости при изгибе для симметричного цикла напряжений, τ -1 – предел выносливости при кручении для симметричного цикла напряжений, кσ – коэффициент концентрации нагрузки для нормальных напряжений, кτ – коэффициент концентрации нагрузки для касательных напряжений, εσ – масштабный фактор для нормальных напряжений, ετ – масштабный фактор для касательных напряжений, β – коэффициент, учитывающий шероховатость поверхности, ψσ, ψτ – коэффициенты, учитывающие соотношение между пределами выносливости при симметричном и пульсационным циклами напряжений. σ -1 = 250 (МПа); τ -1 = 140 (МПа); к σ = 1,89; к τ = 1,71; ε σ = 0,82; ε τ = 0,82; β = 0,95; ψσ = 0,15; ψτ = 0,1. nσ = 250 / ((1,89 / 0,82∙0,95)∙10,56 + 0,15∙0) = 10,81 nτ = 140 / ((1,71 / 0,82∙0,95)∙4,78 + 0,1∙4,78) = 14,07 Коэффициенты концентрации напряжений при изгибе 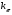 и кручении и кручении 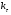 вала вала
Масштабные факторы при изгибе и кручении 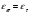
Коэффициент 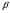
Расчётный коэффициент запаса прочности вала в сечении К – К определяем из выражения: n = nσ∙nτ / (n2σ + n2τ) 1/2; n = 16,59∙22,4 / (16,59 2 + 22,4 2) 1/2 = 13,33. Так как для валов редукторов допускаемое значение n ≥ 2,5, то работоспособность вала при расчёте на выносливость обеспечивается. 3.2.10 Проверка прочности вала в сечении Е – Е. Определяем коэффициент запаса усталостной прочности в сильно нагруженном сечении Е–Е, в котором концентрация напряжений обусловлена канавкой с галтелью. Это сечение расположено на расстоянии 20 мм от сечения К – К. В сечении Е – Е действует изгибающий момент М и = 94,17 (Нм) . Тогда номинальные напряжения в сечении Е – Е: W и. нетто = (π∙d 3 / 32), W к. нетто = (π∙d 3 / 16); W к. нетто = 24,54 (см 3), W и. нетто = 12,27 (см 3). σ а = σ и = М и / W и.нетто, τ а = τm = τ к / 2 = М к /( 2∙ W к. нетто), σ а = σ и = 112,49/12,27 = 9,16 (МПа), τ а = τm = 219,07 /( 2∙24,54) = 4,46 (МПа), σm = 0. Коэффициенты запаса прочности вала в сечении Е – Е по нормальным nσ и касательным nτ напряжениям определяем по формулам: n σ = σ -1 / ((к σ / ε σ∙β)∙σа + ψ σ∙σm), n τ = τ -1 / ((к τ / ε τ∙β)∙τа + ψ τ∙τm); σ -1 = 250 (МПа); τ -1 = 140 (МПа); к σ = 1,55; к τ = 1,42; ε σ = 0,82; ε τ = 0,82; β = 0,95; ψσ = 0,15; ψτ = 0,1. nσ = 250 / ((1,55 / 0,82∙0,95)∙9,16 + 0,15∙0) = 15,19 nτ = 140 / ((1,42 / 0,85∙0,95)∙4,46 + 0,1∙4,46) = 18,61 Расчётный коэффициент запаса прочности вала в сечении Е – Е: n = nσ∙nτ / (n2σ + n2τ) 1/2; n = 11,77 Следовательно, прочность вала в сечении Е – Е также обеспечена.
С целью компенсации радиальных, осевых и угловых смещений валов при эксплуатации привода, тихоходный вал редуктора и вал шестерни открытой зубчатой передачи соединены зубчатой муфтой (МЗ), типоразмер которой выбираем по диаметру вала редуктора с учетом ограничения: 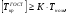 где К - коэффициент режима работы; Т. - номинальный длительно действующий момент (Т2) К = 1,1... 1,4 - при спокойной работе и небольших разгоняемых массах (приводы конвейеров, испытательны установок); К = 1,5...2,0 - при переменной нагрузки и средних разгоняемых массах (поршневые компрессоры, мельницы, металлорежущие станки); К = 2,5.. .4,0 - при ударной нагрузке и больших разгоняемых массах (молоты, прокатные станы). В нашем случае, при диаметре d = 42 мм выбираем по ГОСТ 50895-96 муфту МЗ с Ткр = 0,71 кН • м , так как при Т2= 219,07 Нм, К = 1,5 получим: Трасч = 1,5∙219,07 = 328,6 Нм 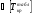 . .Следовательно, прочность муфты обеспечена. Для соединения вала электродвигателя с быстроходным валом редуктора используем упругую втулочно-пальцевую муфту (МУВП), типоразмер которой выбираем по величине наибольшего диаметра соединяемых валов с учетом ограничения Ткр<[Ткр], где Ткр -крутящий момент на валу (Т1); [Ткр] - табличное значение крутящего момента для выбранной муфты. В нашем случае при диаметре d = 42 мм выбираем по ГОСТ 21424-93 муфту МУВП с 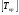 = 250Н • м >Т1=114,12 Нм. = 250Н • м >Т1=114,12 Нм. Поскольку в данном случае применяется стандартная муфта, проверку на смятие ее упругого элемента и пальцев на изгиб не производим.
Выбранные ранее шпонки проверим на смятие рабочих поверхностей. Расчет сводится к выполнению условия в 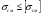 , ,где [ 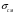 ] - допустимые напряжения смятия. ] - допустимые напряжения смятия.Если ступица стальная, то [ 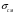 ] = 100…150 Мпа; ] = 100…150 Мпа; если ступица чугунная - [ 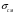 ] = 60...90 Мпа. ] = 60...90 Мпа.Меньшие значения допускаемых напряжений принимают при передаче неравномерных или ударных нагрузок. Напряжение смятия найдем по формуле: 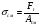 ; ;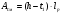 ; ;Где Ft - окружная сила, 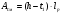 - расчетная площадь смятия паза в ступице, - расчетная площадь смятия паза в ступице,h - высота шпонки, t1 - глубина паза вала, lp – расчетная длина шпонки (для призматических шпонок со скругленными концами lp = l – b, где l – стандартная длина шпонки; b – ширина шпонки). lp = 45-14 = 31 (мм) Асм = (9-5,5)∙31= 108,5 Ft = 2620,92 Н 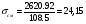 5.2 Проверка шпонок на срез. Напряжения среза найдем по формуле: 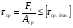 Где Аср = b·l – площадь среза шпонки, b - ширина шпонки, l – стандартная длина шпонки, 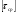 - допускаемое напряжение среза, - допускаемое напряжение среза,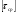 = 60…100 Мпа (меньшие значения принимают при неравномерной или ударной нагрузке). = 60…100 Мпа (меньшие значения принимают при неравномерной или ударной нагрузке).Ft = 2620,92 (Н) Аср = 14·45 = 630 (мм2) 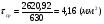 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

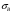
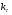 при
при 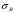
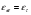 при диаметре вала
при диаметре вала 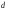 ,мм
,мм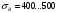 )
)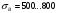 )
)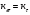 при
при 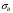 =400…500 МПа
=400…500 МПа