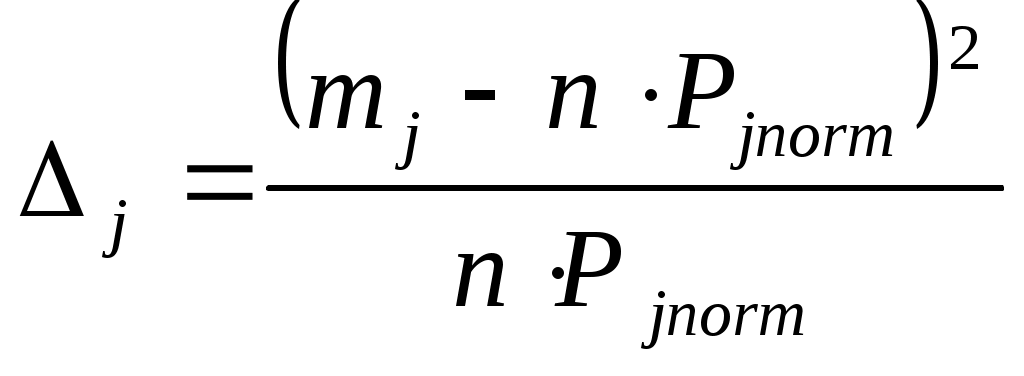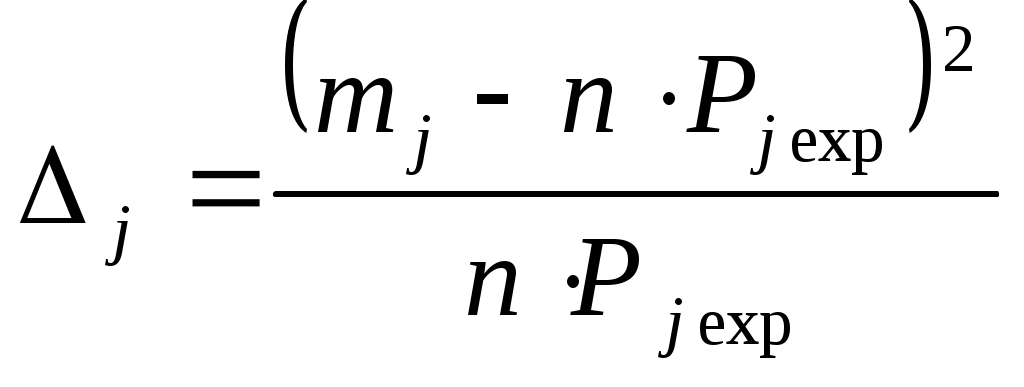Расчет показателей надежности. Отчет о выполнении РАСЧЕТ. Расчет показателей надежности радиоэлектронных систем по результатам испытаний

• Название: Расчет показателей надежности радиоэлектронных систем по результатам испытаний
• Анкор: Расчет показателей надежности
• Дата: 15.09.2022
• Размер: 475.5 Kb.
• Имя файла: Отчет о выполнении РАСЧЕТ.doc
• Тип: Документы; #678173
• страница: 6 из 6

Составляем таблицу 11 для РЭС 1 с новыми интервалами, где: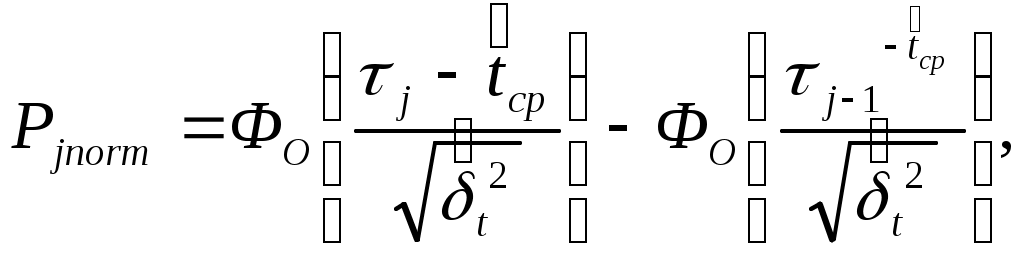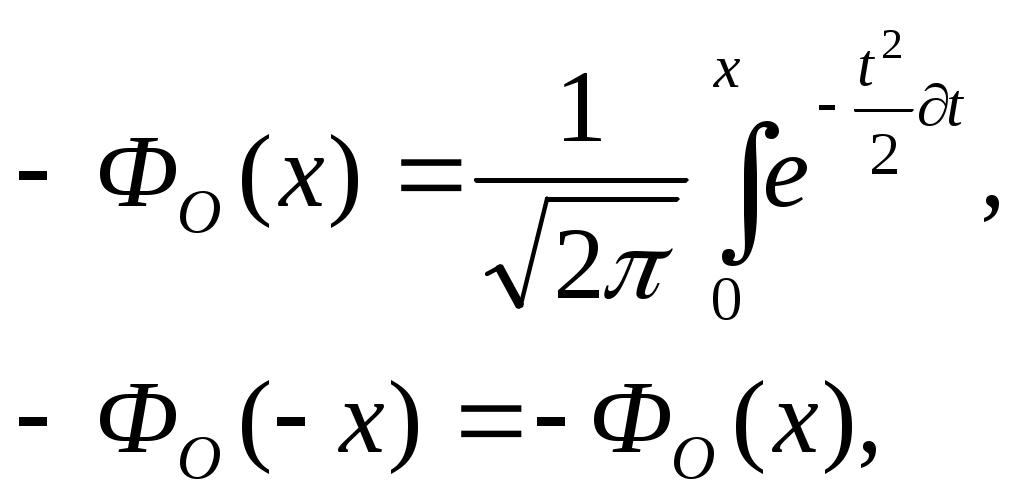

- теоретическое значение вероятности попадания случайной величины в интервал разбиения для нормальной и экспоненциальной модели соответственно;

-



- - значение статистики Пирсона.

Число интервалов разбиения выбирается так, чтобы число попаданий случайной величины в интервал . При следует объединить соседние интервалы.

Гипотеза об адекватности теоретической модели отвергается, если



где - точка - распределения с степенями свободы и заданным уровнем значимости .

- уровень значимости критерия, равный вероятности отвергнуть верную гипотезу (ошибка 1 рода);

- число степеней свободы,

- число параметров распределения ( - для экспоненциального распределения, - для нормального распределения).

Таблица 11

Для РЭС 1
j	mj	Рjnorm		Pjexp
1	8	0,067343503	10,45253	0,005306	285,7386
2	9	0,025712974	61,78254	0,003843	509,0503
3	7	0,023183829	39,76591	0,003451	341,0616
4	6	0,015713484	45,90419	0,0025	348,1279
5	9	0,011497671	158,5825	0,001811	1100,515
			316,4877		2584,493

Значение статистики Пирсона получено для нормального распределения (∆k=316,487)и экспоненциального распределения (∆k=2584,493).

Значение уровня значимости задано: q=0,1.

Число степеней свободы определим по формуле :

для нормального распределения r=5-2-1= 2;

для экспоненциального распределения r=5-1-1=3.

Для нормального распределения =4,602

>4,602, таким образом, гипотеза об адекватности нормального распределения (нормальной модели) отвергается т.к. выполнено .

Для экспоненциального распределения =4,602

>4,602, таким образом, гипотеза об адекватности экспоненциального распределения (экспоненциальной модели) отвергается т.к. выполнено .
Составляем таблицу 12 для РЭС 2 с новыми интервалами.
Таблица 12

Для РЭС 2
j	∆τj	mj	Pjexp
1	24	8	0,009479	153,1736
2	45	8	0,007264	204,5439
3	66	5	0,005567	102,4887
4	87	6	0,004266	199,1203
5	129	7	0,002506	474,9922
6	255	6	0,000508	1761,32
				2895,639

Значение статистики Пирсона, полученное для экспоненциального распределения, ∆k=2895,639. Число степеней свободы определим по формуле:

для экспоненциального распределения r=6-1-1=4.

Для экспоненциального распределения =7,773.

>7,773, значит гипотеза об адекватности экспоненциального распределения (экспоненциальной модели) отвергается т.к. выполнено .
Вывод: на данном этапе осуществлялась проверка согласия эмпирических распределений теоретическим моделям по критерию Пирсона. Анализ полученных результатов показал, что гипотеза об адекватности теоретической модели анализируемых последовательностей выборок для РЭС1 и РЭС2 отвергается.

5.2 Проверка по критерию Колмогорова-Смирнова
Данные для РЭС 1 в таблице 13.
Таблица 13

j	∆τj	F*j	Fjexp	Fjnorm
1	52	0,075	0,398488	8,391868	0,323488	8,316868
2	63	0,2	0,459811	2,1466	0,259811	1,9466
3	74	0,25	0,514882	0,834075	0,264882	0,584075
4	85	0,375	0,564338	0,056043	0,189338	0,318957
5	96	0,425	0,608753	0,338008	0,183753	0,086992
6	107	0,6	0,64864	0,608964	0,04864	0,008964
7	118	0,675	0,68446	0,792147	0,00946	0,117147
8	129	0,725	0,716629	0,971994	0,008371	0,246994
9	140	0,75	0,745518	1,092398	0,004482	0,342398
10	151	0,875	0,771462	1,131855	0,103538	0,256855
11	162	0,95	0,794761	1,209484	0,155239	0,259484
12	173	0,975	0,815684	1,312885	0,159316	0,337885
					0,323488	8,316868
					2,045918	52,60049

Для экспоненциальной модели :

= 1,36, 2,045918>1,36

Для нормальной модели :

= 1,36, 52,60049>1,36

Данные для РЭС 2 представлены в таблице 14.

Таблица 14

j	∆τj	F*j	Fjexp
1	24	0,2	0,263919	0,063919
2	45	0,4	0,43703	0,03703
3	66	0,525	0,569429	0,044429
4	87	0,675	0,67069	0,00431
5	108	0,75	0,748137	0,001863
6	129	0,85	0,80737	0,04263
7	150	0,875	0,852673	0,022327
8	171	0,9	0,887321	0,012679
9	192	0,925	0,913821	0,011179
10	213	0,95	0,934088	0,015912
11	234	0,975	0,949589	0,025411
12	255	1	0,961445	0,038555
				0,063919
				0,404261

Для экспоненциальной модели :

= 1,36, 0,404261<1,36

Вывод: на данном этапе осуществлялась проверка согласия эмпирических распределений теоретическим моделям по критерию Колмогорова-Смирнова. Анализ полученных результатов показал, что гипотеза об адекватности нормального распределения (нормальной модели) для РЭС 1 отвергается. Гипотеза об адекватности экспоненциального распределения (экспоненциальной модели) для РЭС 1 отвергается, а для РЭС 2 не отвергается. Таким образом, построенная экспоненциальная модель для РЭС 2 является адекватной реальному распределению.

6. Интервальное оценивание величины средней наработки на отказ
При экспоненциальном распределении наработки на отказ: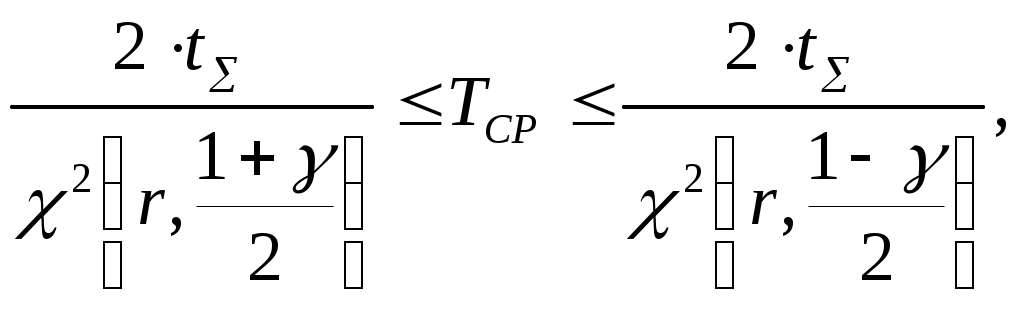



- где - коэффициент доверия;

- - число степеней свободы - распределения.

При нормальном распределении наработки на отказ, учитывая симметрию кривой теоретического распределения, при заданном коэффициенте доверия :

,

где - процентная точка нормального распределения.

Для РЭС 1:

84,74≤T_ср≤127,32 при =0,8;

94,72≤T_ср≤109,88 при =0,9.
Для РЭС 2:

64,88≤T_ср≤97,48 при =0,8;

64,63≤T_ср≤90,03 при =0,9.
Вывод: на данном этапе осуществлялось интервальное оценивание величины средней наработки на отказ. Полученные результаты показывают интервал средней наработки на отказ для РЭС1 и РЭС2.

Заключение
В данной работе была исследована вероятностная модель реальных физических процессов, обладающая тем свойством, что хотя результат отдельного наблюдения физической величины х не может быть предсказан с достаточной точностью, значение функции от множества результатов повторных наблюдений может быть предсказано с существенной точностью. Такая функция называется статистикой, а указанное свойство физического процесса его статистической устойчивостью. Статистическая устойчивость есть эмпирический физический закон, который может быть проверен только опытным путём.