кори №1. Расчет стального настила

• Название: Расчет стального настила
• Дата: 14.11.2021
• Размер: 0.58 Mb.
• Имя файла: кори №1.docx
• Тип: Документы; #271407
• страница: 2 из 7

+++++++++++++++++++++++

4. 
   Расчет главной балки
   

1. 
   Подбор сечения балки
   

Подберем сечение сварной главной балки для балочной клетки. Материал балки – сталь марки ВСт3пс6-2 (табл. П1) с R_y= 260 МПа = 26 кН/см² для листа t=11÷20 мм и R_s = 150 МПа = 13,5 кН/см²; вес настила и балок настила q₁ = 1,13 кН/м² . Предельный прогиб (f /l) = 1/400 (0,0025); шаг главных балок В = 5,8 м; пролет L = 13,5 м. Максимально возможная строительная высота перекрытия – h_стр = 1,75 м.

Расчет производим на равномерно распределенную нагрузку, эквивалентную по интенсивности сосредоточенным грузам. Определяем нормативную и расчетную нагрузки на балку (рис. 3, а):

qⁿ = (pⁿ + gⁿ)·k·В = (16 + 1,13)·1,02·5,5 = 101,4 кН/м;

q = (γ_fp·pⁿ+ γ_fg·gⁿ)·k·В = (1,2·16 + 1,05·1,13)·1,02·5,8 = 175 кН/м,

где k – коэффициент, учитывающий собственный вес балки, ориентировочно 1 – 2%, В – шаг балок.

Определяем расчетный изгибающий момент в середине пролета

М_max = ql²/8 = 175·18²/8 = 7087,5 кН·м = 708 750 кН·см.

Поперечная сила на опоре

Q_max= ql/2 = 175 · 18/2 = 1575 кН.

Определяем требуемый момент сопротивления балки с учетом развития пластических деформаций. Предварительно принимаем с₁ = 1,1:

W_d= М_max/(с₁·R_y·γ_c) = 708 750/(1,1·23·1) = 28 014 см³.

Определяем оптимальную высоту балки, предварительно задав h≈ (1/12)l=

= (18/12) = 1,5м и рассчитав толщину стенки по формуле t_w = 7 + 3h/1000мм = 7 + 3 ·

1500/1000 = 10,5 мм. Принимаем толщину стенки 12 мм.

h_opt=k · √ W/t_w = 1,15 · √ 28 014/1,2 = 175,7 см.

Минимальную высоту балки определяем по формуле:

h_min= (5/24) · (c₁· R_y ·l/E) · [l/ f] · (pⁿ + gⁿ)/( γ_fp·pⁿ+ γ_fg·gⁿ) = (5/24) · (1,1 ·

· 23 · 1800/2,06 · 10⁴) · [400] ·146,7/175 = 154,4 см.

Строительную высоту балки определяем исходя из максимально возможной заданной высоты перекрытия и его конструкции

h_гб = h_стр– h_бн– t_d = 190 – 30 – 1,0 = 159 см.

Сравнивая полученные высоты, принимаем высоту балки h= 160 см, на 1 см больше h_гб.

Проверяем принятую толщину стенки:

t_w= 7 + 3 · 1600/1000 = 11,8 мм;

из условия работы стенки на касательные напряжения на опоре по формуле

t_w = (3/2) · (Q_max/h · R_s) = 3 ·1575/2 · 160 · 13,5= 1,09 см.

Чтобы не применять продольных ребер жесткости, необходимо выполнение

условия t_w≥ (h_w· √R_y/E)/5,5, t_w= (154 · √23/2,06 · 10⁴)/5,5 = 0,94 см.

Сравнивая полученную расчетным путем толщину стенки с принятой (12 мм), приходим к выводу, что она удовлетворяет условию прочности на действие касательных напряжений и не требует укрепления ее продольным ребром жесткости для обеспечения местной устойчивости.

Размеры горизонтальных поясных листов находим исходя из необходимой несущей способности балки. Для этого вычисляем требуемый момент инерции сечения балки

I = W · h/2 = 28 014 · 160/2 = 2 241 120 см⁴.

Находим момент инерции стенки балки, принимая толщину поясов 3 см:

h_w=h – 2t_f = 160– 2 · 3 = 154 см;

I_w= t_wh_w³/12 = 1,2 · 154³/12 ≈ 365 230 см⁴.

Момент инерции, приходящиеся на поясные листы,

I_f= I – I_w = 2 241 120 – 365 230 = 1 875 890 см⁴.

Момент инерции поясных листов балки относительно ее нейтральной оси I_f ≈ 2A_f(h_ef/2)², где А_f – площадь сечение пояса. Моментом инерции поясов относительно их собственной оси ввиду его малости пренебрегаем.

Отсюда получаем требуемую площадь сечения поясов балки

А_f= 2I_f/h_ef² = 2 · 1 875 890/157² = 152,2 см,

где h_ef= h – t_f = 160 – 3 = 157 см.

Тогда b_f= А_f/ t_f = 152,2/3 = 50,7 см. Ширину листа поясов принимаем по таблицы П16. Ближайший больший размер 53 см.

Таким образом, принимаем пояса из универсальной стали 530 х 30 мм, для которой b_f/h = 530/1600 = 1/3,02 находится в пределах рекомендуемого отношения (1/2 -1/5). Уточняем принятый ранее коэффициент учета пластической работы с исходя из

А_f= b_f· t_f= 53 · 3 = 159см²; А_w= h_w· t_w = 154 · 1,2 = 184,8 см²;

А_f/А_w = 159/184,8 = 0,860.

По табл. П5 принимаем с₁= 1,084, которое близка к ранее принятому с₁= 1,1.

Проверяем принятую ширину (свес) поясов по формуле

b_ef /t_f = [(b_f – t_w)/2]/t_f = [(53 – 1,2)/2]/ 3 = 8,63 < 0,11 · h_ef /t_w = 0,11 · 157/1,2 =

= 14,39 < 0,5 · √ E/R_y= 14,96.

Проверяем несущую способность балки по формуле

М ≤ R_y · γ_c · h_ef²· t_w· (А_f/А_w+ α)

исходя из устойчивости стенки в области пластических деформаций балки в месте действия максимального момента, где Q и τ= 0:

λ_w = (h_w/t_w) · √ R_y/E = (154/1,2) · √ 23/2,06 · 10⁴ = 4,29;

М_max= 708 750 < R_y · γ_c · h_ef²· t_w· (А_f/А_w+α) = 23 · 1 · 157²· 1,2 · (159/184,8+

+0,203) =723 440 кН·см,

где α = 0,24 – 0,15(τ/R_s)² – 8,5·10^-3·(λ_w-2,2)² = 0,24 – 8,5·10^-3(4,29 – 2,2)² = 0,203.

Подобранное сечение балки проверяем на прочность. Для этого определяем момент инерции и момент сопротивления балки

I = I_w+ I_f= I_w+ 2b_f·t_f·(h_ef /2)² = 365 230 + 2·53·3·(157/2)² = 365 230 + 1 959 600 ≈ ≈2 324 830 см⁴.

W = 2·I / h = 2·2 324 830/160 = 29 060 см³.

Наибольшее нормальное напряжение в балке

σ = М_max / (с₁·W)= 708 750/(1,084·29 060) = 22,50 кН/см² < R_y = 23 кН/см².

Недонапряжение составляет (23-22,5)·100% / 23 = 2,2 % < 5 %.

Подобранное сечение балки удовлетворяет проверке прочности и не имеет недонапряжение больше 5%. Проверку прогиба балки делать не нужно, так как принятая высота сечения больше минимальной и регламентированный прогиб будет обеспечен.

Сечение главной балки приведено на рис. 3.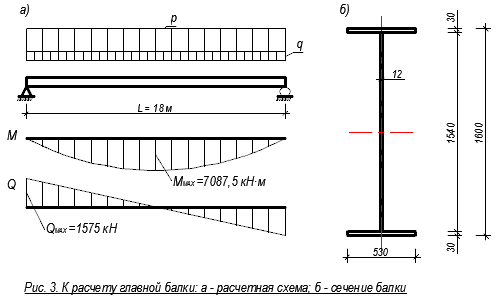



3.2. Изменения сечения главной балки

При равномерно распределенной нагрузке наивыгоднейшее по расходу стали место изменения сечения поясов однопролетной сварной балки находится на расстоянии х ≈ (1/5 ÷ 1/6)l = (1/5 ÷ 1/6)·18 =3,6÷3м от опоры.

Место изменения сечения принимаем на расстоянии х = 3 м от опоры (рис. 4). Сечение изменяем уменьшением ширины поясов. Разные сечения поясов соединяем сварным швом встык электродами Э46 без применения физических методов контроля, т.е. для растянутого пояса R_wy = 0,85R_y = 0,85·23 = 19,55 кН/см².

Определяем расчетный изгибающий момент и перерезывающую силу в сечении:

х =l/6 = 18/6 = 3 м;

М₁ = [q · x · (l – x)]/2 = [175·3 ·(18-3)]/2 = 3937,5 кН ·м = 393 750 кН · см;

Q₁ = q · (l/2 – x) = 175 · (18/2 – 3) = 1050 кН.

Подбор измененного сечения ведем по упругой стадии работы материала по формуле

W_d= М_max/ R_y · γ_c.

Определяем требуемый момент сопротивления и момент инерции

измененного сечения исходя из прочности сварного стыкового шва, работающего на растяжение:

W_d1 = М₁ / R_wy= 393 750/19,55 = 20 140 см³;

I_d1 =W_d1· h/2 = 20140 · 160/2 = 1 611 200 см⁴.

Определяем требуемый момент инерции поясов (I_w= 365 230 см⁴):

I_f1= I_d1 – I_w= 1 611 200 – 365 230 = 1 245 970 см⁴

Требуемая площадь сечения поясов А_f1 определяется из формулы

I_f1 = А_f1· (h_ef /2)²· 2 = А_f1· h_ef²/2; А_f1 = 2 · I_f1/h_ef² = 2 · 1 245 970 /157² =

= 101 cм².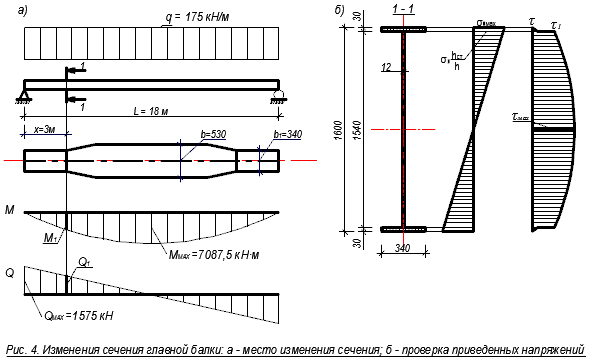



Принимаем пояс 340 х 30 мм, А_f1 = 34 · 3 = 102 см². Принятый пояс удовлетворяет рекомендациям b_f1 >18 см; b_f1 >h/10 = 160/10 = 16 см и b_f1 >b_f/2 =

=53/2 = 26,5 см.

Определяем момент инерции и момент сопротивления уменьшенного сечения (рис. 4):

I₁ = I_w+ 2 · b_f1· t_f· (h_ef /2)² = 365 230 + 2 · 34 · 3 · (157/2)² = 365 230 +

+1 257 100 = 1 622 330 см⁴.

W₁ = 2 · I₁/h = 2 ·1 622 330/160 = 20 279 см³.

Наибольшие напряжения в месте изменения сечения балки равны:

σ₁ = М₁/W₁ = 393750/20279 = 19,42 кН/см² < R_wy = 0,85 · 23 = 19,55 кН/см².
3.3. Проверка и обеспечение общей устойчивости балки

1. 
   Проверка прочности балки.
   

Проверяем максимальные нормальные напряжения в поясах в середине балки по формуле

σ = М_maqx / с₁W= 708 750 / 1,084 ·29 060 = 22,50 кН/см² < R_y = 23 кН/см².

Проверяем максимальные касательные напряжения в стенке на опоре балки по формуле

τ= Q_{max ·} S₁ / I₁ · t_w = 1575 · 11564 /1 622 300 · 1,2 = 9,36 кН/см² < R_s= 13,5 кН/см²,

статический момент полусечения балки

S₁ = b_f1· t_f· h_ef/ 2 + t_w· h_w² / 8 = 34 · 3 · 157 / 2 + 1,2· 154² /8 = 8007 + 3557=

=11564 см³.

Проверяем местные напряжения в стенке под балками настила по формуле

σ_loc = F / t_w·l_loc= 169,4 / 1,2 · 19,5 = 7,24 кН/см²,

где F = Q_max^бн · 2 = 84,70 · 2 = 169,4 кН – опорные реакции балок настила; l_loc = b + 2 · t_f = 13,5 + 2 · 3 = 19,5 см – длина передачи нагрузки на стенку балки.

Ввиду наличия местных напряжений, действующих на стенку балки, надо проверять совместное действие нормальных, касательных и местных напряжений по формуле

σ_red= √ σ₁² + σ_loc– σ₁ · σ_loc+ 3 ·τ₁² ≤ 1,15 · R_y · γ_c

на уровне поясного шва (рис. 4, б) под балкой настила, по уменьшенному сечению вблизи места изменения сечения пояса. Под ближайшей балкой настила будет стоят ребро жесткости, которое воспримет давление балок настила, и передачи давления на стенку в этом месте не будет, поэтому проверяем приведенные напряжения по формуле

σ_red= √ σ₁² + 3 ·τ₁² ≤ 1,15 · R_y · γ_c

в сечении 1 – 1 - месте изменения сечения балки (где они будут максимальны):

σ_red= √ σ₁² + 3 ·τ₁² = √ 18,69² + 3 · 4,32² = √ 349,3 + 56 = 20,1 ≤

≤ 1,15 · R_y · γ_c = 1,15 · 23 · 1 = 26,45 кН/см²;

σ₁ = (М₁ / W₁) · (h_w/ h) = (393 750 / 20 279) · (154 / 160) = 19,42 · 0,9625 =

= 18,69 кН/см²;

τ₁ = (Q₁ · S_f1) / (I₁ ·t_w) = (1050 · 8007) / (1 622 330 · 1,2) = 4,32 кН/см²;

S_f1 = b_f1 · t_f · (h_ef / 2) = 34 · 3 · (157/2) = 8007 см³.

Прочность балки обеспечена.

2. 
   Проверка общей устойчивости балки.
   

Проверка общей устойчивости балки в месте действия максимальных нормальных напряжений, принимая за расчетный пролет l₀- расстояние между балками настила: в середине пролета балки, где учтены пластические деформации, проверяем применимость формулы (7.14) [ 1 ]: 1 <h/b_f= 160/53 = 3,02 < 6 и b_f/t_f= 53/3 = 17,7 < 35:

l₀/ b = 100/53 = 1,89 < δ· [ 0,41 + 0,0032 · b_f/t_f + (0,73 – 0,016 · b_f/t_f ) · b_f/h_ef ] · √ E/R_y=

= 0,3 · [0,41 + 0,0032 · 53/3 + (0,73 – 0,016 · 53/3) · 53/157] · √ 2,06 · 10⁴/23 =

= 0,3 · [0,41 + 0,0565 + 0,1510] · 29,927 = 5,54,

где δ = [ 1 – 0,7· (с₁ – 1) / (с-1)] = 0,3, так как τ= 0 и с₁ = с. В месте уменьшенного сечения балки (балка работает упруго и δ = 1); l₀ = 100 см – расстояние между балками настила

l_ef/ b_f1 = 100 / 34 = 2,94 < 1 · [0,41 + 0,0032 · 34 / 3 + (0,73 – 0,016 · 34 /3) · 34 / 157] · √ 2,06 · 10⁴ / /23 = 1 · [0,41 + 0,0362 + 0,1188] · 29,927 = 16,91.

Обе проверки показали, что общая устойчивость балки обеспечена.

3. 
   Проверка прогиба балки может не производиться, так как принятая высота балки больше минимальной h = 160 см > h_min= 154,4 см.
   

3.4. Проверка местной устойчивости элементов балки

1. Устойчивость сжатого пояса

Проверка устойчивости сжатого пояса производится в месте максимальных нормальных напряжений в нем – в середине пролета балки, где возможны пластические деформации. Проверка производиться по формуле

b_ef/ t_f ≤ 0,11 · h_ef/ t_w, но не более 0,5 · √ E / R_y.

Рассчитываем h_ef/ t_w = 157 / 1,2 = 130,8 > 2,7 · √ E / R_y = 2,7 · √ 2,06 ·10⁴ / 23 = 80,8; b_ef/ t_f= (53 – 1,2) / (3 · 2) = 8,63 < 0,11· h_ef/t_w= 0,11 · 157 / 1,2 = 14,39, т.е. местная устойчивость пояса обеспечена.

2. Устойчивость стенки

Первоначально определяем необходимость постановки ребер жесткости по формуле λ_w= (h_w/ t_w) · √ R_y / E = (154 / 1,2) · √ 23 / 2,06 · 10⁴ = 4,29 > 2,2, т.е. вертикальные ребра жесткости необходимы. Кроме того, в зоне учета пластических

деформаций необходима постановка ребер жесткости под каждой балкой настила, так как местные напряжения в стенке в этой зоне недопустимы. Определяем длину зоны использования пластических деформаций в стенке по формуле:

а =l· √ 1 – (1 / c₁) · (h / h_w) = 1800 · √ 1 – (1/1,084) · (160 / 154) = 366,9 см.

Расстановку вертикальных ребер жесткости принимаем по рис. 5.

Нормами разрешается не проверять устойчивость стенок балок с поперечными ребрами жесткости для балок с двусторонними поясными швами и местной нагрузкой на пояс при λ_w ≤ 2,5. Устанавливаем необходимость проверки устойчивости стенки. Расчет λ_w= 4,29 > 2,5 показал, что проверку устойчивости стенки следует производить.

Проверяем отсек «а». В соответствии с расшифровкой к формуле (7.46) [ 3 ] определяем средние значения М и Q в сечении 2 – 2 на расстоянии х = 350 см от опоры (под балкой настила), что почти совпадает с рекомендацией расстояния в h_ef/ 2 от края отсека:

М₂ = [q · х · (l– х)] / 2 = [175 · 3,5 · (18– 3,5)] / 2 = 4 440 кН·м = 444 000 кН·см;

Q₂ = q·(l/ 2– х) = 175 · (18 /2 – 3,5) = 963 кН.

Определяем действующие напряжения

σ = (М₂ / W) · (h_w/ h) = (444 000/ 29 060) · (154/ 160) = 14,7 кН/см^2;

τ= Q₂ / (h_w ·t_w) = 963 / (154 · 1,2) = 5,2кН/см²;

σ_loc= 7,24 кН/см².

Определяем критические напряжения. По формуле (7.40) [ 3 ] находим

τ_cr= 10,3 · (1 + 0,76 / μ²) · R_s/ λ_ef² = 10,3 · (1 + 0,76 / 1,95²) ∙13,5/4,29² = 9,06 кН/см²,

где h_ef= h_w; λ_ef = λ_w= 4,29; μ = а / h_ef= 300 / 154 = 1,95, R_s= 13,5 кН/см². σ_loc/ σ = 7,24 /14,7 = 0,49. По формуле (7.44) [ 3 ] определяем

δ = β · (b_f/ h_ef) · (t_f/ t_w)³ = 0,8 · (53 / 154) · (3 / 1,2)³ = 4,30.

По табл. П8 при δ = 4,30 и а / h_ef= 1,95 предельное значение σ_loc/ σ = 1,177. Расчетное значение σ_loc/ σ = 0,49 < 1,177, поэтому σ_crопределяем по формуле (7.45) [ 3 ]:

σ_cr= (с_cr ·R_y) / λ_w² = (34,63 · 23) / 4,29² = 43,27 кН/см²,

где с_cr= 34,63 получено по табл. П6 при δ = 4,30.

По формуле (7.48) [ 3 ] определяем σ_loc.cr, подставляя в нее из табл. П7 значение а / 2 вместо а:

σ_loc.cr = (c₁ · R_y) / λ_а² = (21,6 · 23) / 4,18² = 28,4 кН/см²,

где λ_а = (а/ 2 · t_w) · √ R_y / E= (300 / 2 · 1,2) · √ 23 / 2,06·10⁴ = 4,18; По табл. П7 при δ = 4,3, а / 2h_w = 300 / 2 · 154 = 0,974 с₁ = 21,02.

Теперь подставляем все значения в формулу (7.47) [ 3 ]

√ (σ / σ_cr+ σ_loc/ σ_loc.cr)² + (τ/ τ_cr)² = √ (14,7 / 43,27+ 7,24 / 28,4)² + (5,2/ 9,06)² =

√ (0,340+ 0,255)² + 0,574² = √ 0,354+ 0,329 = √ 0,683 = 0,83 < γ_c = 1.

Проверка показала, что устойчивость стенки обеспечена.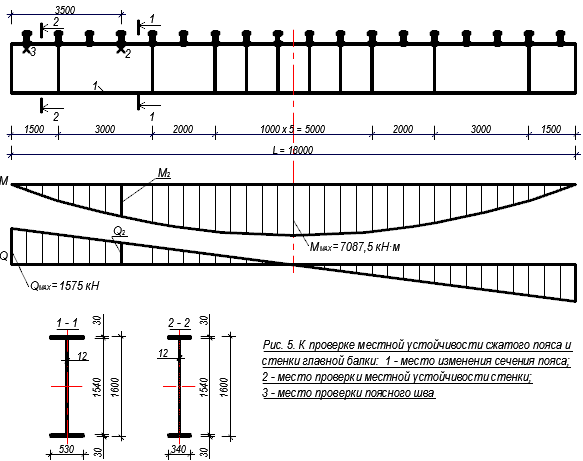



3.5. Соединение поясов балки со стенкой

Так как балка рассчитана с учетом пластических деформаций, то швы выполняем двусторонние, автоматической сваркой в лодочку, сварочной проволокой Св – 0,8ГА. По формуле (7.57) [ 3 ] определяем толщину шва в сечении х = 50 см (рис. 5), под первой от опоры балкой настила, где сдвигающая сила максимальна

k_f= [ 1 / n · (β · R_w)_min] · √ (Q · S_f / I)² + (F / l_loc)² = (1 / 2 · 18,4) · √ (1575 · 8007 / 1 622 330)² + (169,4 / 19,5)² = 0,02717 · √ 60,42 + 75,46 = 0,316см.

По табл. П2 определяем R_wf= 200 МПа = 20 кН/см², а по табл. П1 R_wz = 160МПа = 16 кН/см². По табл. П3 определяем β_f = 1,1, β_z = 1,15. Далее определяем более опасное сечение шва

β_fR_wf = 1,1 · 20 = 22 кН/см² > β_z · R_wz = 1,15 · 16 = 18,4 кН/см².

Значения Q, I, F, l_locвычислены ранее.

S_f = b₁ · t_f · (h_ef / 2) = 34 · 3 · (157/2) = 8007 см³.

По табл. П4 принимаем минимально допустимый при толщине пояса t_f= 30 мм шов k_f= 7 мм, что больше получившегося по расчету k_f = 3,16 мм.

3.6. Расчет монтажного стыка главной балки на высокопрочных болтах

Стык выполняем в середине пролета балки, где М = 7087,5 кН·м и Q = 0, конструкция стыка представлена на рис. 6.

Стык осуществляем высокопрочными болтами d = 24 мм из стали 38ХС «селект», имеющий R_bun =1350 МПа = 135 кН/см² (табл. П9); обработка поверхности газопламенная. Несущая способность болта, имеющего две плоскости трения, по формуле (6.4) [ 3 ]

Q_bh = R_bh· А_bn· (γ_b· μ / γ_h) · k_s = 94,5 · 3,52 · (0,85 · 0,42 / 1,02) · 2 = 232,8 кН,

где R_bh = 0,7 · R_bun= 0,7 · 135 = 94,5 кН/см², А_bn = 3,52 см² (табл. П10); γ_b= 0,85, так как разница в номинальных диаметрах отверстия и болта больше 1 мм; μ = 0,42 и γ_h = 1,02 (табл. П11); принимая способ регулирования натяжения болта по углу закручивания, k_s = 2 – две плоскости трения.

Стык поясов. Каждый пояс балки перекрываем тремя накладками сечениями 530 х 16 мм и 2 х 245 х 16 мм, общей площадью сечения

А_н = 1,6 · (53 + 2 · 24,5) = 163,2 см² > А_f= 53 х 3 =159 см².

Усилие в поясе определяем по формуле (7.62)

М_f = М · I_f / I = 7087,5 · 1 959 600 / 2 324 830 = 5974 кН·м;

N_f = М_f / h_ef = 5974 / 1,57 = 3 805 кН,

где I, I_f и h_ef– определены выше.

Количество болтов для прикрепления накладок рассчитывается по формуле (7.63)

n = N_f /Q_bh = 3805 / 232,8 = 16,3

Принимаем 18 болтов и размещаем их согласно рис. 6.

Стык стенки. Стенку перекрываем двумя вертикальными накладками сечением 430 х 1460 х 8 мм.

Момент, действующий на стенку, определяем по формуле (7.64) [3]:

М_w= М · I_w/ I = 7087,5 · 365 230 / 2 324 830 = 1 113 кН·м.

Принимаем расстояние между крайними по высоте рядами болтов

a_max= 1540 –2 · 110 = 1320 мм.

Из формулы (7.66) находим коэффициент стыка α

α = М_w/ (m· а_max· Q_bh) = 111 300 / (2 · 132 · 232,8) = 1,81.

Из табл. П12 находим количество рядов болтов по вертикали k при α = 1,81, k = 9 и α = 1,87 > 1,81. Принимаем 9 рядов с шагом 165 мм. Проверяем стык стенки по формуле (7.65) [ 1 ]:

N_max= М_w· а_max / (m· ∑ а_i²) = 1 113 ·1,32 / ( 2 · 3,267) = 224,8 кН < Q_bh = 232,8 кН,

где ∑ а_i²= 0,33² + 0,66² + 0,99² + 1,32² = 0,1089 + 0,4356 + 0,9801 + 1,7424 = 3,267 м².

Проверяем ослабление нижнего растянутого пояса отверстиями под болты d_О = 27 мм (на 3 мм больше диаметра болта). Пояс ослаблен двумя отверстиями по краю стыка

А_fn = 3,0 · (53 – 2 · 2,7) = 142,8 см² > 0,85 · А_f = 0,85 ·53 · 3 = 135,2 см².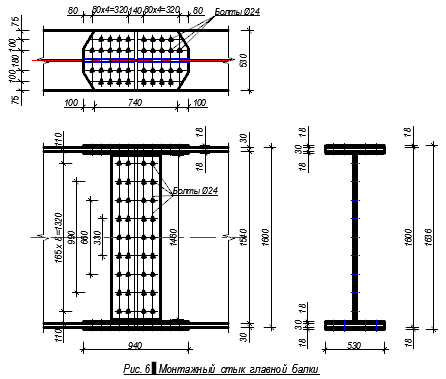



Ослабление пояса можно не учитывать.

Проверяем ослабление накладок в середине стыка четырьмя отверстиями

А_n^накл = 163,2 – 4 · 2 · 1,6 · 2,7 = 163,2 – 34,56 = 128,64 см² <

< 0,85 · А_f = 0,85 · 53 · 3 = 135,2 см².

Приходится увеличивать толщину накладок. Принимаем накладки толщиной 18 мм

А_n^накл = 1,8 · (53 + 2 · 24,5) – 4 · 2 · 1,8 · 2,7 = 183,6 – 38,88 = 144,72 см² >

> 0,85 · А_f= 135,2 см².