задача. Головня И.И. ЭСб-20-1 Задача 19. Расчет установившегося режима разомкнутой электрической сети матричным методом с использованием нелинейных уравнений узловых напряжений в форме баланса токов в узлах Задание

• Название: Расчет установившегося режима разомкнутой электрической сети матричным методом с использованием нелинейных уравнений узловых напряжений в форме баланса токов в узлах Задание
• Анкор: задача
• Дата: 18.05.2022
• Размер: 396.59 Kb.
• Имя файла: Головня И.И. ЭСб-20-1 Задача 19.docx
• Тип: Документы; #535705

Головня И.И. ЭСб-20-1 Вариант 13

Раздел 3. Расчет установившегося режима разомкнутой электрической сети матричным методом с использованием нелинейных уравнений узловых напряжений в форме баланса токов в узлах
Задание:

Рассчитать параметры установившегося режима разомкнутой электрической сети (рисунок 2.1) матричным методом с использованием нелинейных уравнений узловых напряжений в форме баланса токов в узлах.

3.1 Исходные данные

Разомкнутая электрическая сеть: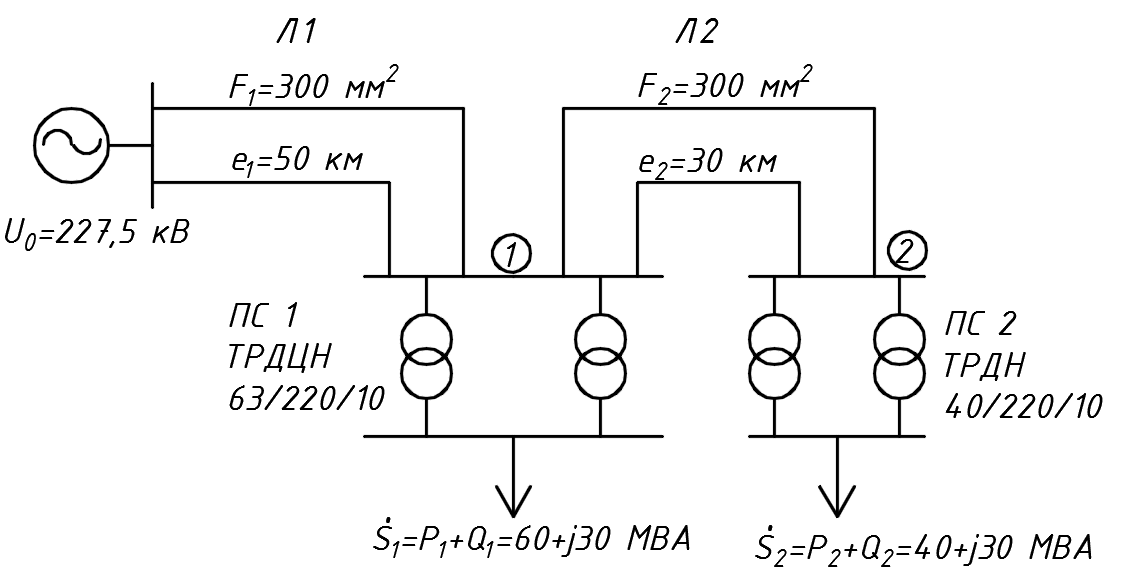

Рисунок 3.1. - Схема разомкнутой электрической сети

Определить:

1. Потоки(токи) и потери мощности в элементах сети;

2. Напряжение в узлах и падения напряжения в элементах сети.

3.2 Схема замещения

Для линии 220 кВ составляем схему замещения (рисунок 3.2) без учёта потерь активной мощности на корону (то есть без активных поперечных проводимостей в схемах замещения линий).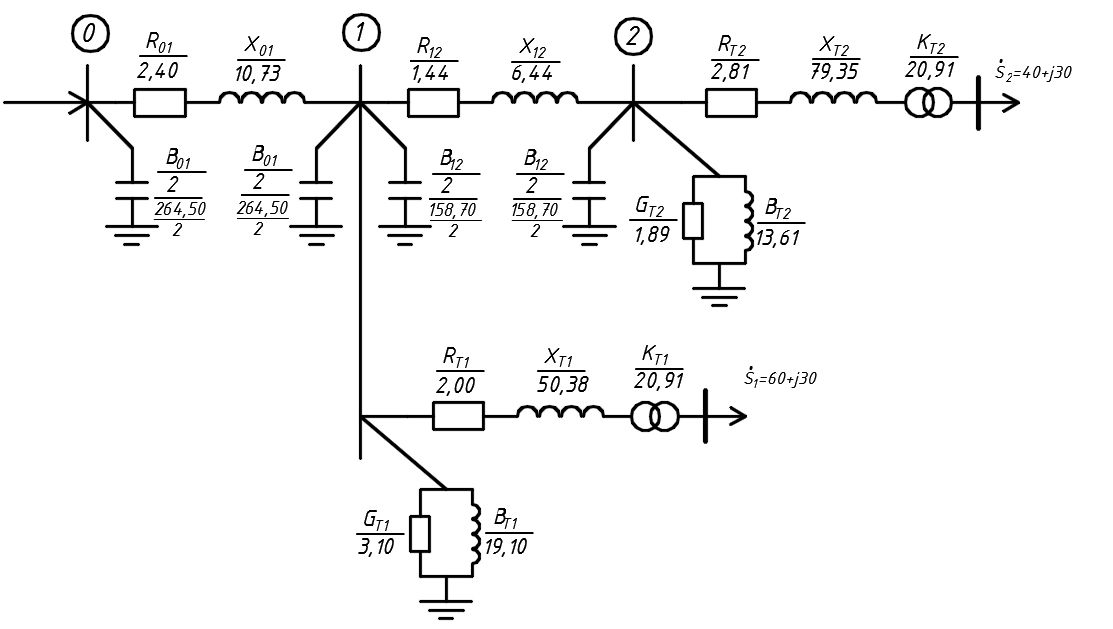



Рисунок 3.2. - Схема замещения разомкнутой сети
Подробный расчет параметров схемы замещения приведен ниже

Рассчитаем активное и реактивное сопротивления, и емкостную проводимость в линиях:

Определяем параметры схемы замещения

ВЛ-1

Активное сопротивление: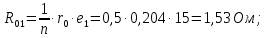


Индуктивное сопротивление: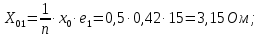


Ёмкостная проводимость: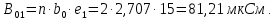


ВЛ-2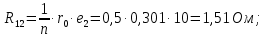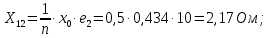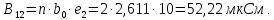






ПС 1-ТРДН-40/110/10

Активное сопротивление: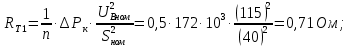


Индуктивное сопротивление: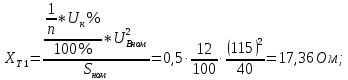


Активная проводимость: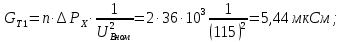


Ёмкостная проводимость: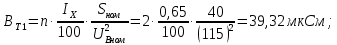


Коэффициент трансформации: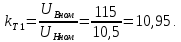


ПС 2-ТРДН-40/110/10
Активное сопротивление: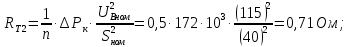


Индуктивное сопротивление: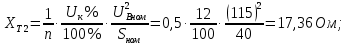


Активная проводимость: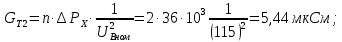


Емкостная проводимость: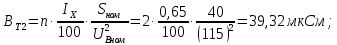


Коэффициент трансформации: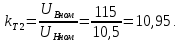



3.3 Граф электрической сети

Для расчёта установившегося режима электрической сети матричным методом составляем граф сети (см. рис. 3.3). Величины проводимостей ветвей графа рассчитываем, исходя из определённых ранее параметров схемы замещения.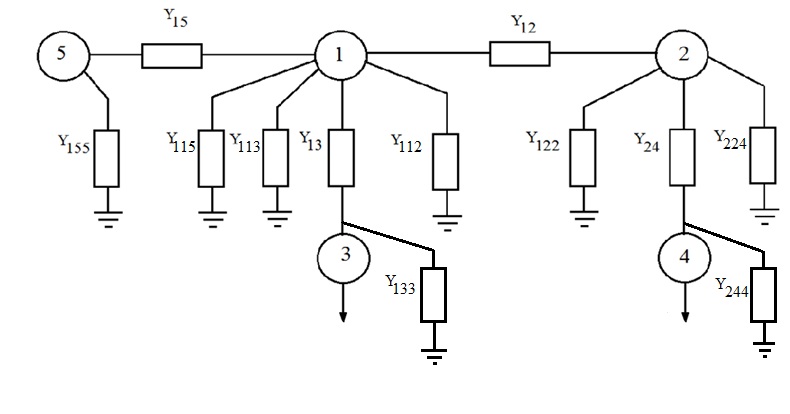

Риунок. 3.3 – Граф заданной электрической сети
Проводимости ветвей графа сети: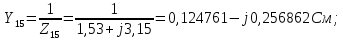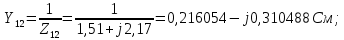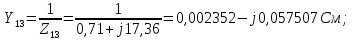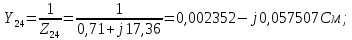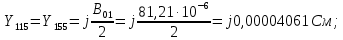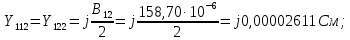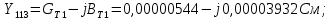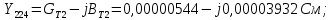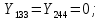









Проводимости узлов графа сети: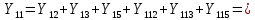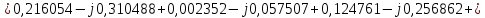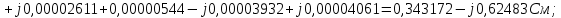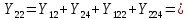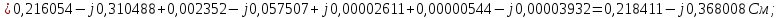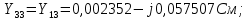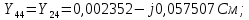










Квадратная матрица собственных и взаимных проводимостей узлов графа сети имеет вид: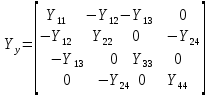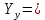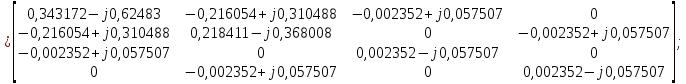





3.4 Формирование уравнений узловых напряжений

Для расчёта установившегося режима воспользуемся уравнениями узловых напряжений в форме балансов токов в узлах. Запишем их в общем матричном виде:

(1)
Составим матрицы, входящие в выражение (1):
Матрица собственных и взаимных проводимостей: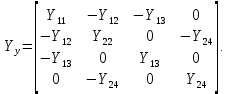

Вектор-столбец узловых напряжений: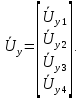



Обратная диагональная матрица напряжений в узлах: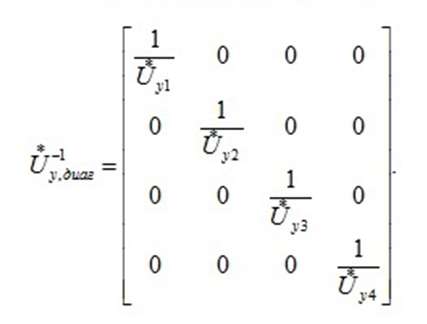


Вектор-столбец заданных мощностей в узлах: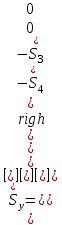
.
Вектор-столбец проводимости базисного узла: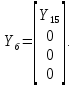


Напряжение базисного узла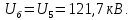
Получаем следующую систему: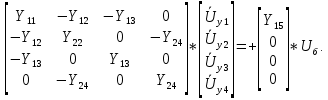



Преобразуем правую часть к одному вектор-столбцу: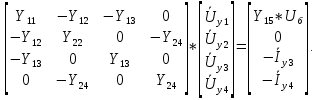

Найдем обратную матрицу собственных и взаимных проводимостей: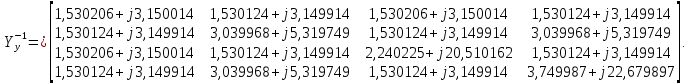


3.5 Численное решение систем нелинейных уравнений методом линеаризации

Зададимся начальными приближениями напряжений в узлах 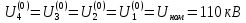и точностью вычислений .
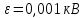Алгоритм решения:

1. Вычисляем приближения токов в узлах .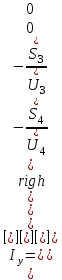
2. Вычисляем обратную матрицу проводимостей :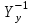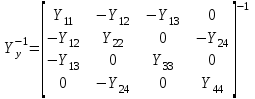

.

3. Вычисляем узловые напряжения по формуле:

U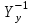_у= ·I_у= · .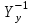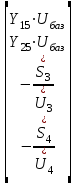

4. Проверяем условие окончания: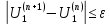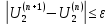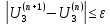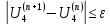

;

;

;

.

Если хотя бы одно из условий не выполняется, возвращаемся к пункту 1.
Итерационный процесс

Вычислим значения элементов вектор-столбца, находящегося в правой части системы, при выбранных начальных приближениях. Решим полученную систему линеаризованных уравнений методом обратной матрицы.

Первая итерация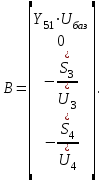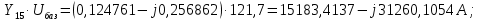





Найдем приближения токов в узлах 3 и 4: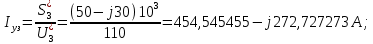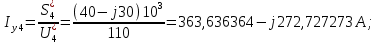





Найдем вектор-столбец B: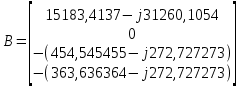

Подставляем вычисленное значение токов в узлах в уравнение узловых напряжений. В результате получаем линеаризованную систему уравнений, которая решается методом обратной матрицы: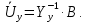

Тогда вектор-столбец узловых напряжений равен:

Проверяем условие окончания: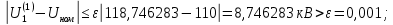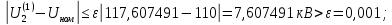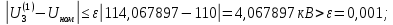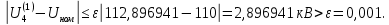







Ни одно из условий окончания не выполняется, переходим ко второй итерации.
Вторая итерация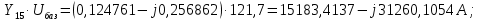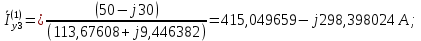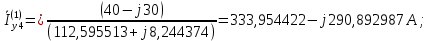






Находим вектор-столбец B: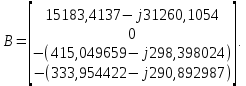

Тогда вектор-столбец узловых напряжений: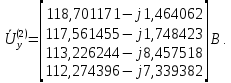

Проверяем условие окончания: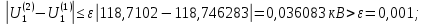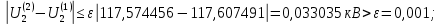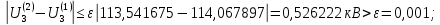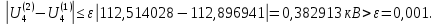







Ни одно из условий окончания не выполняется, переходим к третьей итерации.
Третья итерация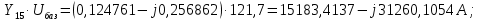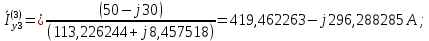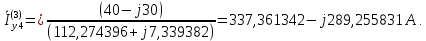



Находим вектор-столбец B: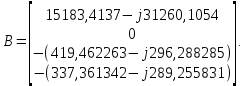


Тогда вектор-столбец узловых напряжений:


Проверяем условие окончания: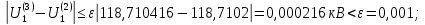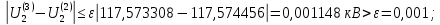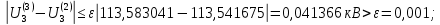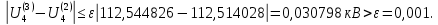







Три условия окончания не выполняются, переходим к четвертой итерации.
Четвертая итерация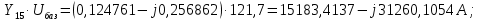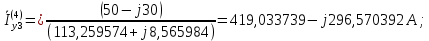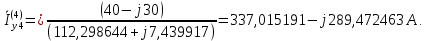




Находим вектор-столбец B: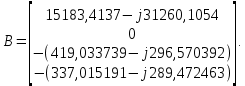


Тогда вектор-столбец узловых напряжений: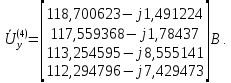

Проверяем условие окончания: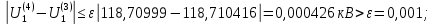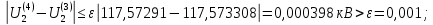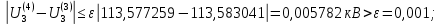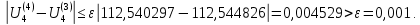








Все условия окончания итерационного процесса выполнены, значит заканчиваем итерационный процесс.
3.6 Определение параметров установившегося режима

Определяем все параметры установившегося режима по известным формулам и наносим их на карту режима (рисунок 3.5).
Ветвь 2-4:
1) Падение напряжение в ветви 2-4: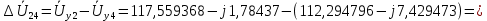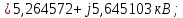

2) Ток в ветви 2-4: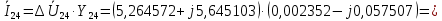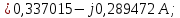


3) Поток мощности в конце ветви 2-4: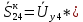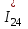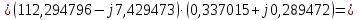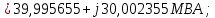


4) Поток мощности в начале ветви 2-4: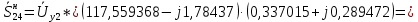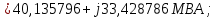


5) Потери мощности в продольных сопротивлениях ветви 2-4: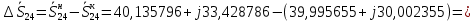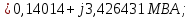

6) Находим потери мощности в поперечных проводимостях ветви 2-4: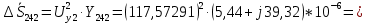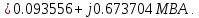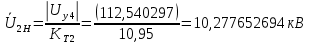



Ветвь 1-2:
1) Падение напряжение в ветви 1-2: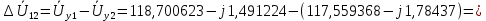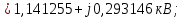

2) Ток в ветви 1-2: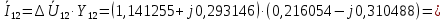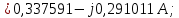


3) Поток мощности в конце ветви 1-2: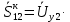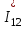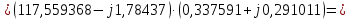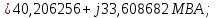


4) Поток мощности в начале ветви 1-2: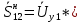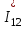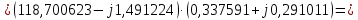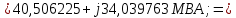


5) Потери мощности в продольных сопротивлениях ветви 1-2: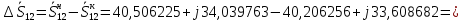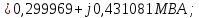

6) Находим потери мощности в поперечных проводимостях ветви 2-4 (зарядная мощность):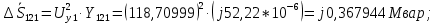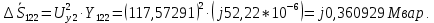



Ветвь 1-3:
1) Падение напряжение в ветви 1-3: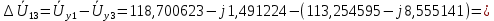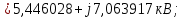


2) Ток в ветви 1-3: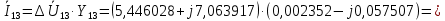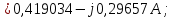


3) Поток мощности в конце ветви 1-3: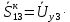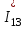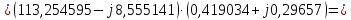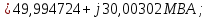


4) Поток мощности в начале ветви 1-3: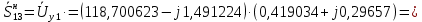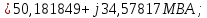


5) Потери мощности в продольных сопротивлениях ветви 1-3: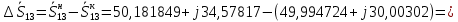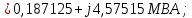


6) Находим потери мощности в поперечных проводимостях ветви 1-3: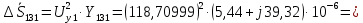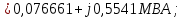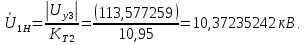



Ветвь 5-1:

1) Падение напряжение в ветви 5-1: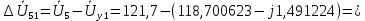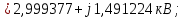


2) Ток в ветви 5-1: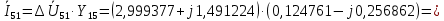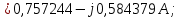


3) Поток мощности в конце ветви 5-1: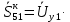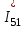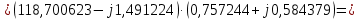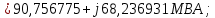


4) Поток мощности в начале ветви 5-1: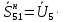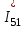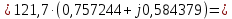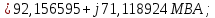


5) Потери мощности в продольных сопротивлениях ветви 5-1: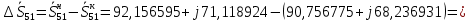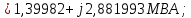

6) Находим потери мощности в поперечных проводимостях ветви 5-1 (зарядная мощность):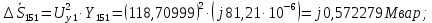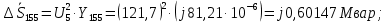


7) Мощность генерации: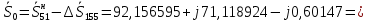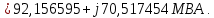



3.7 Баланс мощностей

1) Баланс по активной мощности: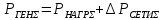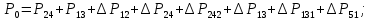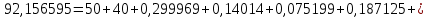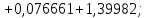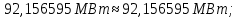
;



2) Баланс по реактивной мощности: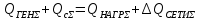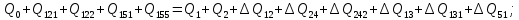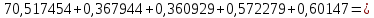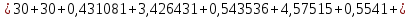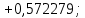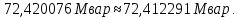





Таблица 3.1 Суммарные показатели установившегося режима

Суммарные показатели установившегося режима	Мощность
	Активная, МВт	Реактивная, Мвар
Генерация
Нагрузка		60
Потери	( %)	12,412291 (20,687151667%)
Зарядная мощность	-	1,902622

Потери активной и реактивной мощности в сети в процентах: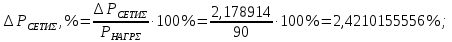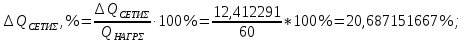





3.8 Карта установившегося режима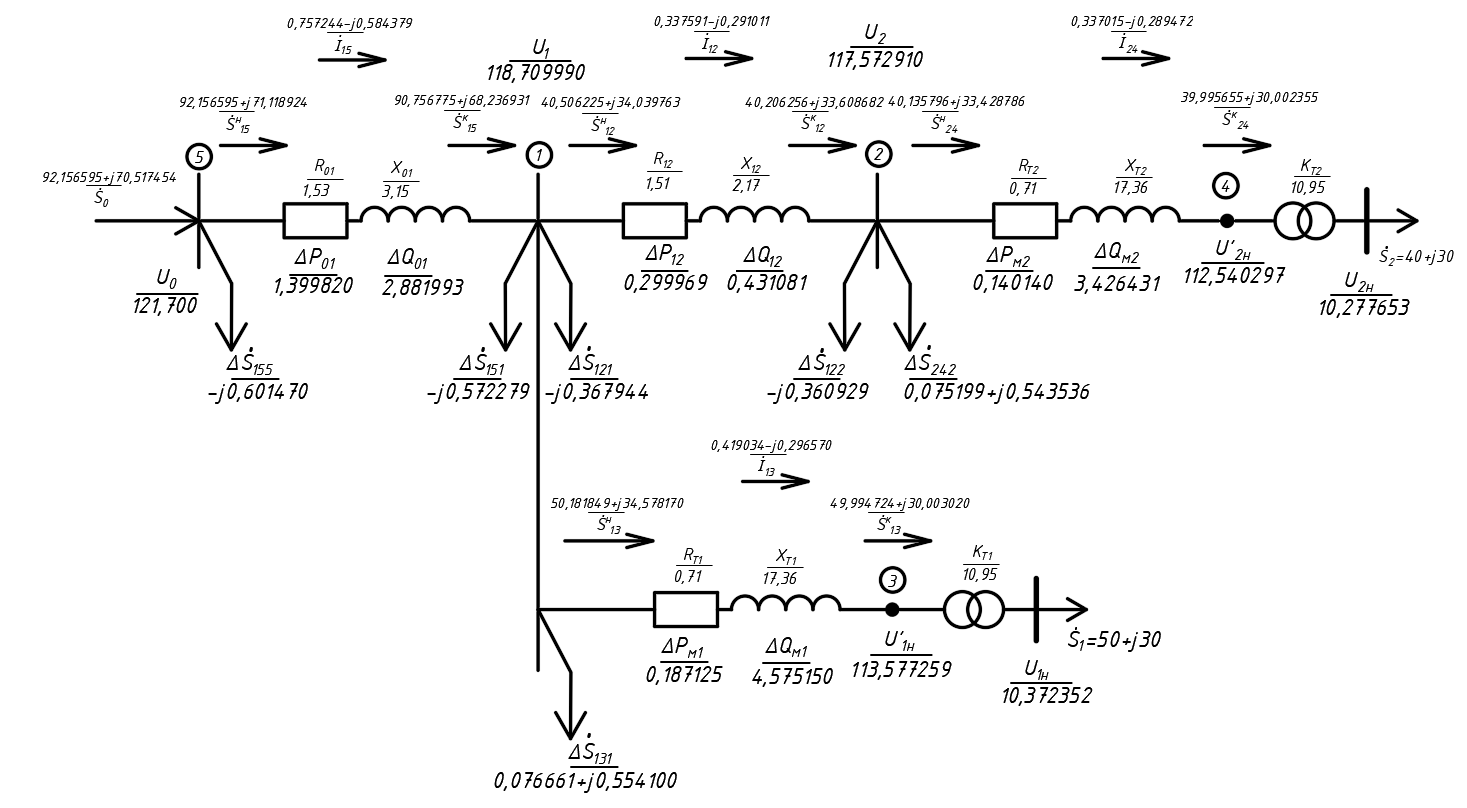


Рисунок 3.4 – Карта установившегося режима
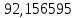
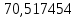
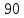
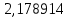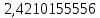