уравнительный резервуар. ПЗ Берлин. Расчеты колебаний уровня в уравнительном резервуаре гэс с дополнительным сопротивлением и определением его размеров
 Скачать 479.2 Kb. Скачать 479.2 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ» Институт гидротехнического и энергетического строительства Кафедра «Гидравлики и гидротехнического строительства» КУРСОВАЯ РАБОТА по теме «Расчеты колебаний уровня в уравнительном резервуаре ГЭС с дополнительным сопротивлением и определением его размеров» Выполнил студент ИГЭС 4 – 12 Симонов М.Д. Руководитель работы Берлин В.В. К защите Работа защищена с оценкой г. Москва 2019 год ОглавлениеВведение 2 Задачи и исходные данные 3 Расчет уравнительного резервуара 4 2.1. Определение критической площади уравнительного резервуара 4 2.2. Подбор оптимального значения коэффициента дополнительного сопротивления 5 2.3. Расчеты колебаний уровня в уравнительном резервуаре 8 2.3.1. Режим сброса максимальной нагрузки 8 2.3.2. Режим набора нагрузки 9 2.4. Вычисление высоты уравнительного резервуара 11 Список литературы 12 ВведениеВ гидроэлектростанциях деривационного типа одним из важнейших элементов, отвечающим за надежную и безаварийную эксплуатацию всего гидросооружения, являются уравнительные резервуары. Любое изменение расхода через напорный деривационный туннель при регулировании нагрузки гидроэлектростанции или при полном ее сбросе (авария, короткое замыкание) влечет за собой изменение скорости воды в нём, а главное - давления. Быстрое изменение давления в туннеле становится причиной гидравлического удара, который в свою очередь, в зависимости от своей силы, может повредить туннель, нарушив его внутреннюю облицовку, или полностью вывести его из эксплуатации. Устройство уравнительных резервуаров в конце напорной деривационной трассы снижает повышенное давление, исключая тем самым негативные последствия гидравлического удара. Наиболее эффективные параметры уравнительных резервуаров находятся из условия их сопряжения с туннелем. Помимо предотвращения повышения давления, уравнительные резервуары также ограничивают и минимальное его значение, которое может способствовать образованию вакуума, что также наносит вред водоводам и турбинному оборудованию. 1. Задачи и исходные данныеВ курсовой работе, исходя из заданных начальных условий, требуется: 1. Определить критическую площадь 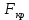 уравнительного резервуара и назначить диаметр уравнительного резервуара и назначить диаметр 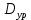 исходя из условия исходя из условия 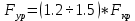 . .2. Подобрать оптимальное значение коэффициента 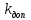 дополнительного сопротивления так, чтобы обеспечить равенство обоих максимумов повышения давления в водоводе при расчетном сбросе нагрузки дополнительного сопротивления так, чтобы обеспечить равенство обоих максимумов повышения давления в водоводе при расчетном сбросе нагрузки 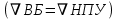 . Использовать значение полученного коэффициента . Использовать значение полученного коэффициента 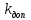 для дальнейших расчетов. для дальнейших расчетов.3. Выполнить расчеты колебаний уровня в уравнительном резервуаре ГЭС для двух режимов: а) сброс максимальной нагрузки при 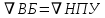 , коэффициент шероховатости принять минимальным для бетонной облицовки – , коэффициент шероховатости принять минимальным для бетонной облицовки – 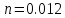 ; определить значение максимального подъема уровня в резервуаре; ; определить значение максимального подъема уровня в резервуаре;б) набор нагрузки от 50% до 100% при 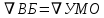 , коэффициент шероховатости принять максимальным для бетонной облицовки – , коэффициент шероховатости принять максимальным для бетонной облицовки – 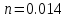 ; определить значение наибольшего опускания уровня в резервуаре. ; определить значение наибольшего опускания уровня в резервуаре.Исходные данные: Отметка НПУ, м = 0. Отметка УМО, м = -18. Отметка нижнего бьефа, м = - 200. Длина деривации Lдер ,м = 2200. Диаметр деривации Dдер ,м = 4,9. Максимальный расход ГЭС Qmax , м3/с = 79. Время изменения расхода при сбросе нагрузки – 10 с. Время изменения расхода при наборе половины сбросе нагрузки (половины расхода) – 15 с. 2. Расчет уравнительного резервуара2.1 Определение критической площади уравнительного резервуараКритическую площадь уравнительного резервуара определим по формуле: 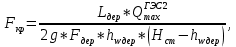 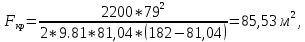 где: 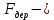 площадь сечения деривации, для круглого трубопровода определяется по формуле: площадь сечения деривации, для круглого трубопровода определяется по формуле: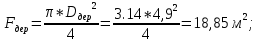 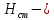 статический напор, определяемый по формуле: статический напор, определяемый по формуле: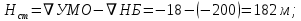 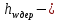 потери напора в деривации, для данного курсового учитываем только потери по длине, рассчитанные по формуле: потери напора в деривации, для данного курсового учитываем только потери по длине, рассчитанные по формуле: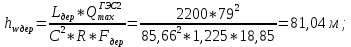 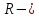 гидравлический радиус, для круглого трубопровода определяется по формуле: гидравлический радиус, для круглого трубопровода определяется по формуле: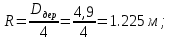 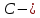 коэффициент Шези, определяемый по формуле: коэффициент Шези, определяемый по формуле: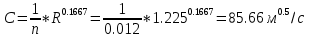 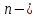 коэффициент шероховатости, для бетонной облицовки принимаем равным коэффициент шероховатости, для бетонной облицовки принимаем равным 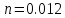 . .Определим площадь уравнительного резервуара 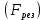 с учетом запаса с учетом запаса 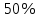 , получаем: , получаем:Fрез = 1,5*85,53 = 128,3 м2; Зная площадь определим диаметр уравнительного резервуара: 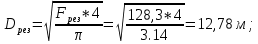 Принимаем диаметр уравнительного резервуара равным Dрез = 13 м. Уточняем площадь уравнительного резервуара: 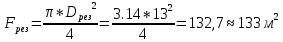 2.2 Подбор оптимального значение коэффициента дополнительного сопротивления Уравнительным резервуаром с дополнительным сопротивлением называют такой резервуар, в основании которого на проходном отверстии устраивается сужающая диафрагма, создающая дополнительные потери напора. Эти потери оказывают существенное влияние как на амплитуду колебаний уровня, так и на экстремумы давления в деривационном водоводе, поэтому при моделировании напорной системы важен их точный учет, путем поиска оптимального коэффициента дополнительного сопротивления. В схемах с уравнительными резервуарами, имеющими дополнительное сопротивление, имеют место три пика давления при закрытии турбины: первый - в момент наибольшего изменения расхода в развилке резервуара; второй — в момент поступления в резервуар наибольшего расхода; третий - в момент достижения уровнем наибольшей отметки. При проектировании уравнительных резервуаров с дополнительным сопротивлением добиваются того, чтобы второй и третий пики совпадали. Для определения локальных максимумов (пиков) давления будем использовать пользоваться программой RESER, которая позволяет рассчитывать колебания в напорной системе. При этом нужно использовать соответствующие граничные условия. Все построения графиков для определения локальных максимумов и оптимального коэффициента дополнительного сопротивления будем осуществлять с помощью программы EXCEL. 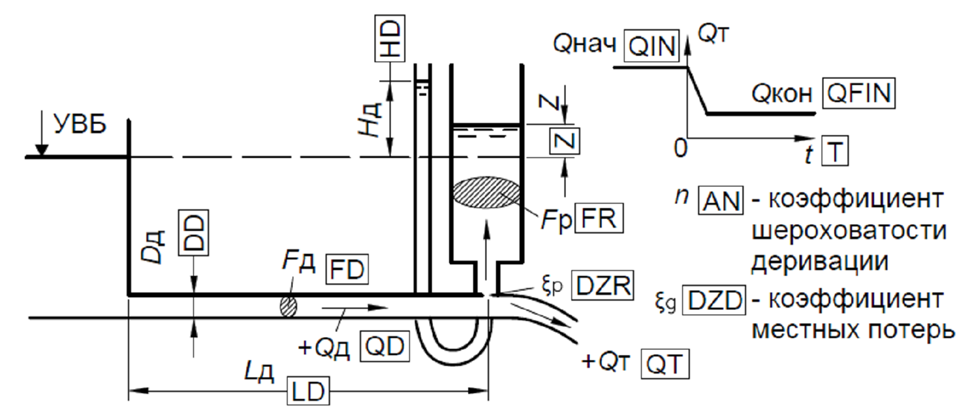 Ниже представлена схема (рис.1) деривационного водовода и уравнительного резервуара с дополнительным сопротивлением, с учетом обозначений в программе RESER: Ниже представлена схема (рис.1) деривационного водовода и уравнительного резервуара с дополнительным сопротивлением, с учетом обозначений в программе RESER:Рис.1 Расчёты будем проводить в следующем порядке: 1. Примем произвольное значение коэффициента дополнительного сопротивления 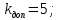 2. Произведем расчеты на сброс нагрузки при этом коэффициенте; 3. Определим значения локальных максимумов давления; 4. Примем значения коэффициента дополнительного сопротивления от 5 до 45 с шагом 5 и повторим пункты 2-3; 5. На основании полученных данных строим графики зависимости локальных максимумов от коэффициента дополнительного сопротивления. 6. За оптимальны коэффициент дополнительного сопротивления принимаем точку их пересечения. Все полученные результаты сведем в таблицу и построим график:
 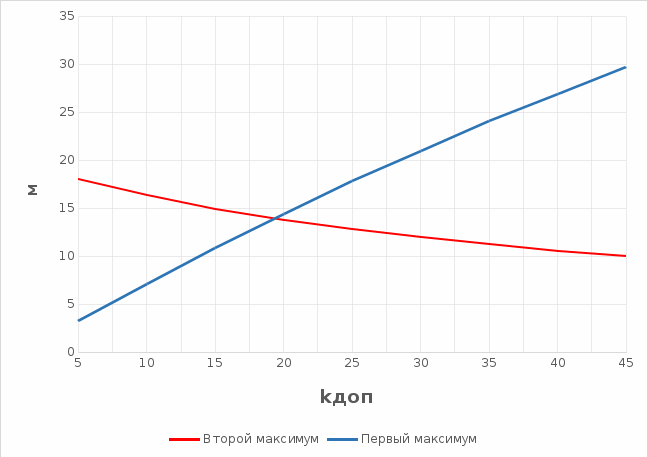 Из графика видно, что значение оптимального коэффициента дополнительного сопротивления исходя из равенства двух максимумов 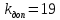 . . 2.3 Расчеты колебаний уровня в уравнительном резервуаре ГЭСДругими важными параметрами, влияющими на разработку конструкции уравнительных резервуаров, являются максимальная zmax и минимальная zmin высоты подъема уровня воды в нём. Значения zmax и zmin достигаются в переходных процессах, которые помимо изменения расхода через ГЭС учитывают также положение уровней верхнего и нижнего бьефа и условия расчета потерь напора. Рассмотрим по отдельности переходные процессы в которых достигаются соответствующие им значения zmax и zmin . 2.3.1 Режим сброса максимальной нагрузкиОтметка zmax в уравнительном резервуаре достигается в переходном процессе сброса нагрузки всеми агрегатами. Для расчета этого переходного процесса уровень верхнего бьефа принимается на отметке НПУ, а коэффициент шероховатости принимается минимальным для бетонной облицовки n = 0,012. Такие значения принимаются, чтобы получить максимальный подъем уровня воды в резервуаре: отметка в верхнем бьефе, т.е. и напор – максимальный, а за счет минимального коэффициента шероховатости будут обеспечены минимальные потери напора на трение по длине. В данном расчетном случае закон изменения расхода следующий: начальный расход соответствует суммарному расчетному расходу через турбины: Qнач = Qmax = 79 м3/с. За конечный принимается нулевой расход, соответствующий полному закрытию направляющего аппарата: Qкон= 0 м3/с. Коэффициент дополнительного сопротивления принимаем ранее найденный оптимальный 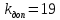 . .Время изменения расхода при сбросе нагрузки – 10 с. Для выполнения данного расчета также используем программу RESER. После расчета получили следующие графики: 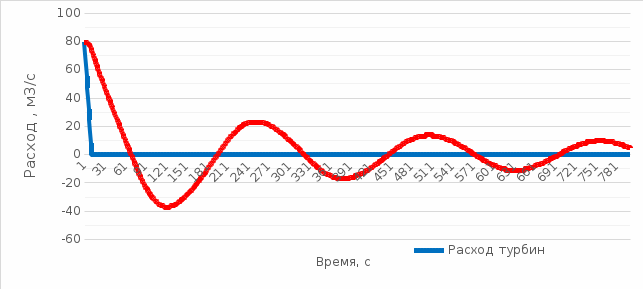 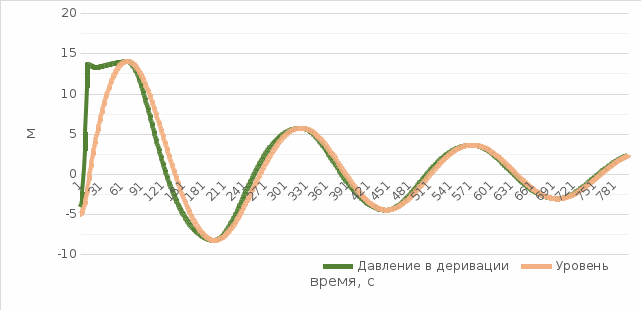 На втором графике наглядно видно, что максимальный уровень подъема воды в уравнительном резервуаре zmax = 14 м. 2.3.2 Режим набора нагрузки Отметка zmin в уравнительном резервуаре достигается в переходном процессе набора нагрузки всеми агрегатами. В данном расчетном случае уровень верхнего бьефа принимается на отметке УМО = - 18 м, коэффициент шероховатости принимается максимальным для бетонной облицовки n =0,014. Такие условия приняты для получения противоположной ситуации по сравнению с первым расчетным случаем: минимальный из возможных напор и максимальные потери на трение по длине, все это способствует минимальному току воды в уравнительный резервуар. В данном расчетном случае закон изменения расхода следующий: начальный расход принимается соответствующим нижней границе регулировочного диапазона, равный 50% от расчетного расход: Qнач = 0,5* Qmax = 0,5*79  40 м3/с; 40 м3/с;За конечный принимается суммарный расчетный расход через турбины: Qкон= Qmax = 79 м3/с. Коэффициент дополнительного сопротивления принимаем ранее найденный оптимальный 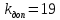 . .Время изменения расхода при наборе половины сбросе нагрузки – 15 с. Для выполнения данного расчета также используем программу RESER. После расчета получили следующие графики: 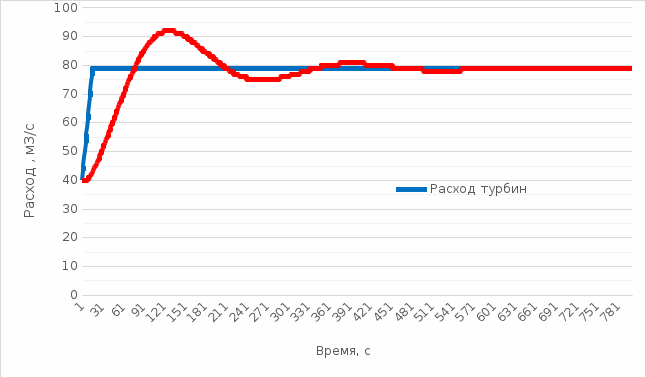 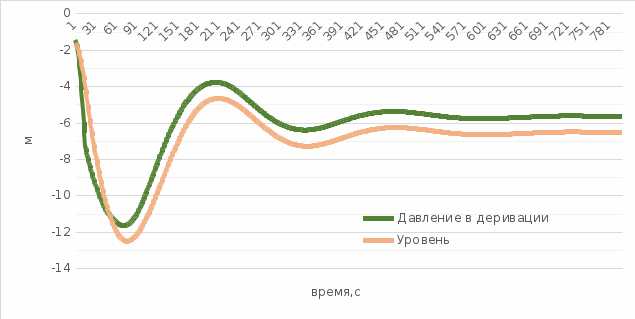 На втором графике наглядно видно, что минимальный уровень опускания воды в уравнительном резервуаре zmin = 12,2 м. 2.4. Вычисление высоты уравнительного резервуара Таким образом, исходя из полученных значений zmax и zmin, можем рассчитать высоту уравнительного резервуара: Нур = zmax + zmin + (1 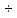 2 м) = 14 + 12,2 + 1,5 = 27,7 м. 2 м) = 14 + 12,2 + 1,5 = 27,7 м. Итоговые размеры уравнительного резервуара представлены на рис. 2. 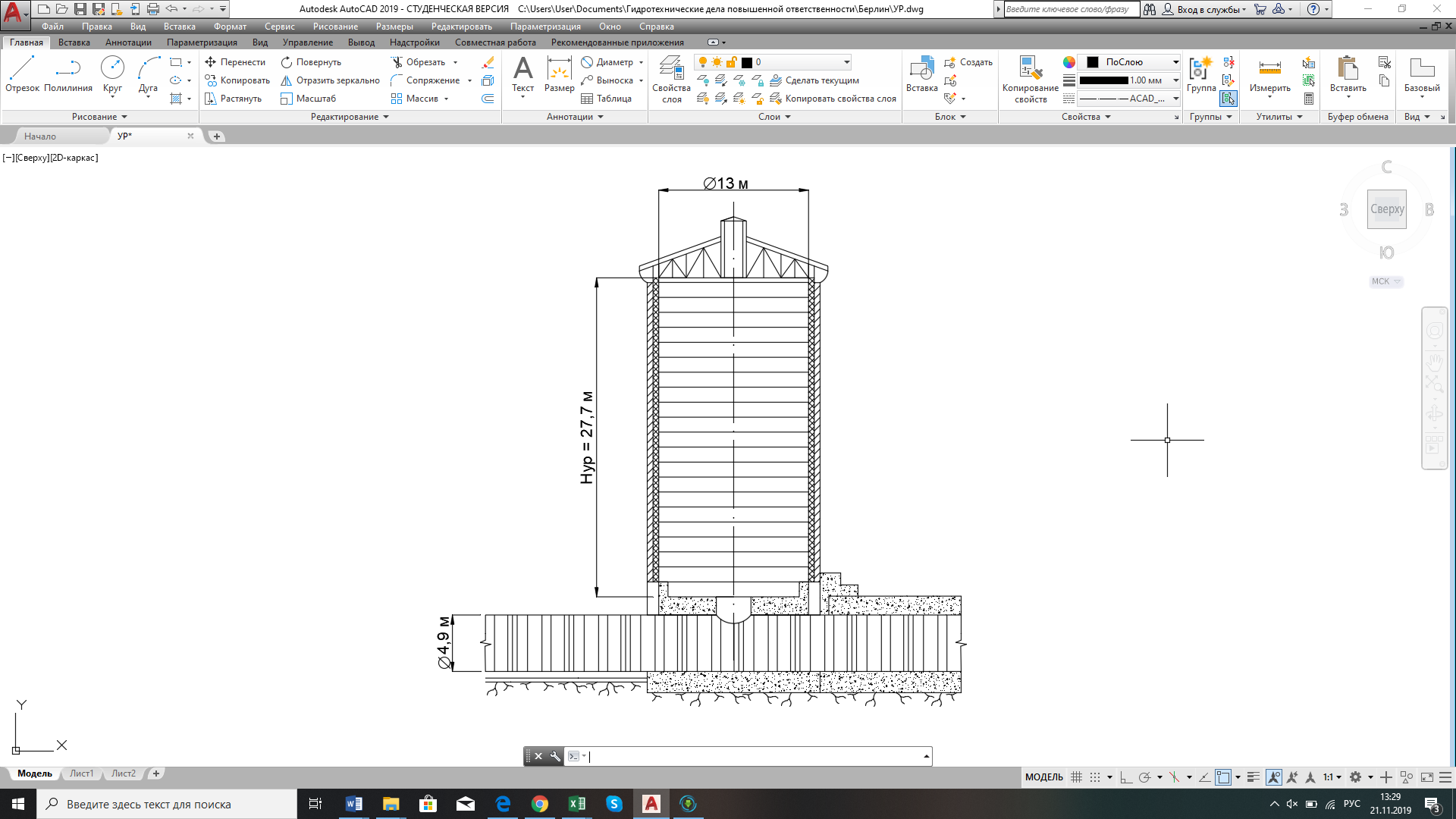 Рис. 2 Рис. 2Список литературы Муравьев О.А. Уравнительные резервуары: Учебное пособие. М.: МГСУ, 2016. – 75 с. Берлин В.В., Муравьев О.А. Переходные процессы на ГЭС с уравнительными резервуарами. М.: Энергоатомиздат, 1991. - 150 с. |
