ГДЗ по алгебре. Расчетно-графическое Задание N1_2019A. Расчетнографические задания по общей физике. 1
 Скачать 3.91 Mb. Скачать 3.91 Mb.
|
|
3. Законы сохранения 3.1. Легендарный железнодорожный транспортер ТМ-1-180 с орудием обеспечивал снаряду массой 97,5 кг начальную скорость 920 м/с. Масса транспортера 160 тонн (Амирханов Л.И. Морские пушки на железной дороге. СПб: Иванов и Лещинский, 1994. –64 с.). Из орудия производят выстрел вдоль железнодорожного пути. Определить на какое расстояние 3.2. Во время осады Севастополя в 1942 году фашисты применили для подавления батареи 305-мм орудий свою самую большую пушку Дора К(Е). Масса бетонобойного снаряда была 7100 кг, начальная скорость – 720 м/с, а масса всего орудия, установленного на железнодорожные рельсы, составляла 1350 тонн. Огонь мог вестись только параллельно железнодорожного пути. Определить на какое расстояние 3.3. Шар массой 1,0 кг бросили с поверхности Земли под углом 300 к горизонту с начальной скоростью 20 м/с. Найти мощность силы тяжести в момент времени t. Чему равна работа силы тяжести за время t? Построить графики мощности и работы как функции времени и определить мощность и работу для момента времени 1.0 с. 3.4. Шар массой 1,0 кг бросили с поверхности Земли под углом 300 к горизонту с начальной скоростью 20 м/с. Найти кинетическую 3.5. Шар массой 1,0 кг бросили с поверхности Земли под углом 300 к горизонту с начальной скоростью 15 м/с. Найти кинетическую 3.6. Дульную (начальную) скорость пули массой 9,6 г можно определить с помощью баллистического маятника. Определите угол отклонения баллистического маятника, если начальная скорость пули 3.7. В момент, когда скорость падающей вниз гранаты составила 4 м/с, граната разорвалась на три одинаковых осколка. Два осколка разлетелись в горизонтальной плоскости под прямым углом друг к другу со скоростью 5 м/с каждый. Найти скорость третьего осколка сразу после разрыва. 3.8. Человек, сидящий в лодке, бросает камень вдоль нее под углом 45 градусов к горизонту. Масса камня 10 кг, масса человека и лодки 100 кг, начальная скорость камня относительно берега 10 м/с. Найти расстояние между точкой падения камня и лодкой в момент, когда камень коснется воды. Считать, что во время полета камня, лодка движется равномерно. 3.9. Охотник массой 80 кг стреляет из карабина с движущейся лодки массой 120 кг по направлению её движения. Пуля массой 20 грамм вылетает со скоростью 800 м/с. Какую скорость имела лодка, если она остановилась после трех следующих друг за другом выстрелов? Построить диаграмму скорости системы «лодка-охотник». 3.10. Охотник массой 80 кг стреляет из карабина с движущейся лодки массой 120 кг в сторону противоположную её движению. Пуля массой 20 грамм вылетает со скоростью 800 м/с. Какую скорость будет иметь лодка, если лодка двигалась со скоростью 0,5 м/с? Построить диаграмму скорости системы «лодка-охотник». 4. Динамика вращательного движения 4.1. Два одинаковых цилиндра одновременно начали движение. Первый цилиндр падает свободно, а второй цилиндр падает, раскручивая предварительно намотанную тонкую гибкую нерастяжимую ленту, массой которой можно пренебречь по сравнению с массой цилиндра, свободный конец ленты закреплен. С какой скоростью упадут цилиндры, если начальная высота равна 10 м. Постройте графики движения цилиндров и определите момент времени, когда расстояние между ними составляет 1 м. 4.2. Два одинаковых цилиндра одновременно начали движение. Первый цилиндр падает свободно, а второй цилиндр падает, раскручивая предварительно намотанную тонкую гибкую нерастяжимую ленту, массой которой можно пренебречь по сравнению с массой цилиндра, свободный конец ленты закреплен. С какой скоростью упадут цилиндры, если начальная высота равна 20 м. Постройте графики движения цилиндров и определите момент времени, когда расстояние между ними составляет 2 м. 4.3. Два одинаковых цилиндра одновременно начали движение. Первый цилиндр падает свободно, а второй цилиндр падает, раскручивая предварительно намотанную тонкую гибкую нерастяжимую ленту, массой которой можно пренебречь по сравнению с массой цилиндра, свободный конец ленты закреплен. С какой скоростью упадут цилиндры, если начальная высота равна 30 м. Постройте графики движения цилиндров и определите момент времени, когда расстояние между ними составляет 3 м. 4.4. На горизонтальную ось насажены маховик и легкий шкив радиусом 5 см. На шкив намотан шнур, к которому привязан груз массой 0.4 кг. Опускаясь равноускоренно, груз прошел путь 1,8 м за время 3 с. Определить момент инерции маховика. Построить график числа оборотов от времени и определить полное число оборотов маховика. 4.5. На горизонтальную ось насажены маховик и легкий шкив радиусом 4 см. На шкив намотан шнур, к которому привязан груз массой 0.8 кг. Опускаясь равноускоренно, груз прошел путь 2,0 м за время 2 с. Определить момент инерции маховика. Построить график числа оборотов от времени и определить полное число оборотов маховика. 4.6. К ободу однородного валика радиусом 0,2 м приложена постоянная касательная сила 100 Н. При вращении на диск действует сила трения, момент которой равен 5,0 Нм. Определить массу диска, если известно, что он вращается с постоянным угловым ускорением 4.7. К ободу однородного валика радиусом 0,25 м приложена постоянная касательная сила 100 Н. При вращении на диск действует сила трения, момент которой равен 8,0 Нм. Определить массу диска, если известно, что он вращается с постоянным угловым ускорением 4.8. Сплошной однородный маховик массой 20 кг и радиусом 100 мм вращается, совершая 20 об/с. С какой силой нужно прижать к нему тормозную колодку, чтобы он остановился за 5 с, если коэффициент трения равен 0.2? Определить работу торможения и построить график угловой скорости и кинетической энергии маховика. 4.9. Сплошной однородный маховик массой 200 кг и радиусом 200 мм вращается, совершая 20 об/с. С какой силой нужно прижать к нему тормозную колодку, чтобы он остановился за 5 с, если коэффициент трения равен 0.2? Определить работу торможения и построить график работы торможения от времени. 4.10. На горизонтальную ось насажены маховик и легкий шкив радиусом 6 см. На шкив намотан шнур, к которому привязан груз массой 0.5 кг. Опускаясь равноускоренно, груз прошел путь 1,5 м за время 3 с. Определить момент инерции маховика. Построить график числа оборотов от времени и определить полное число оборотов маховика. 5. Неинерциальные системы отсчета. Движение тел с переменной массой 5.1. Поезд массой 3500 т движется на северной широте 5.2. Центробежная стиральная машина наполнена мокрым бельем и вращается со скоростью 1200 об/мин. Во сколько раз центростремительная сила к моменту отрыва капли воды от ткани больше веса капли, если капля находится на расстоянии 0.3 м от оси вращения. 5  .3. Поезд движется по закруглению радиусом 500 м. Ширина железнодорожной колеи 152.4 см. Наружный рельс расположен на 12 см выше внутреннего. При какой скорости движения поезда на закруглении колеса не оказывают бокового давления на рельсы? .3. Поезд движется по закруглению радиусом 500 м. Ширина железнодорожной колеи 152.4 см. Наружный рельс расположен на 12 см выше внутреннего. При какой скорости движения поезда на закруглении колеса не оказывают бокового давления на рельсы?5.4. В центре горизонтально расположенного диска радиусом 2 м установлена мишень, а на краю – воздушный пистолет. При неподвижном диске шарик попадает в центр мишени. Если диск вращается вокруг вертикальной оси, проходящей через его центр, с постоянной угловой скоростью 5.5. Сколько времени человек с ранцевым реактивным двигателем за спиной может продержаться на постоянной высоте, если его масса 5.6. Ракета массой 1 т, запущенная с поверхности Земли вертикально вверх, поднимается с ускорением 5.7. Космический корабль имеет массу 3.5 т. При маневрировании из его двигателей вырывается струя газов со скоростью 5.8. После запуска ракета выбрасывает ежесекундно газ массой 90 г со скоростью 5.9. По какому закону должна меняться во времени масса ракеты (вместе с топливом), чтобы она во время работы оставалась неподвижной в поле тяжести Земли, если скорость 5  .10. Для поражения цели с самолета запускают ракету. Самолет летит горизонтально на высоте .10. Для поражения цели с самолета запускают ракету. Самолет летит горизонтально на высоте 5.11. Космический корабль стартует с начальной массой 6. Механические колебания Пример 6.1. Частица массы 0.2 кг находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты где Решение Построим график потенциальной энергии, для уточнения вида кривой найдем точки экстремума 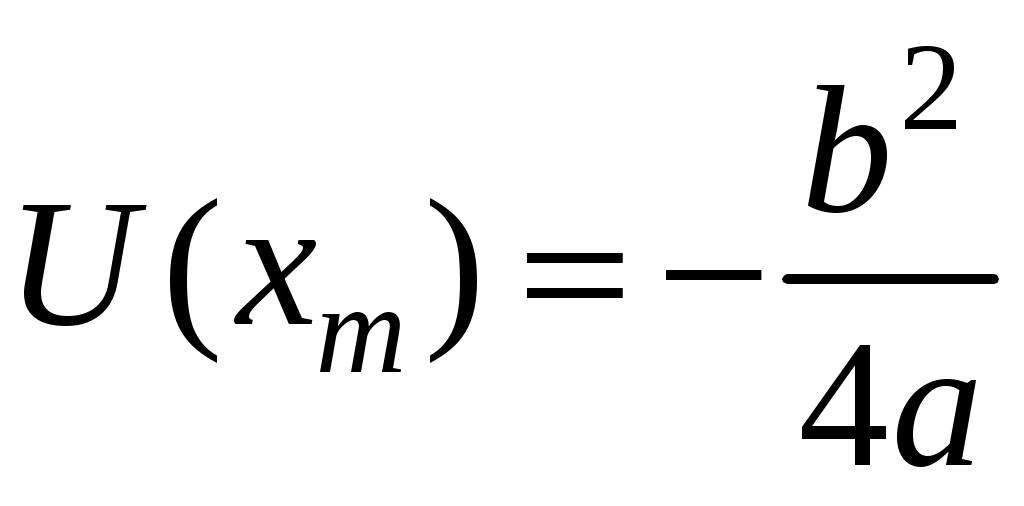 . .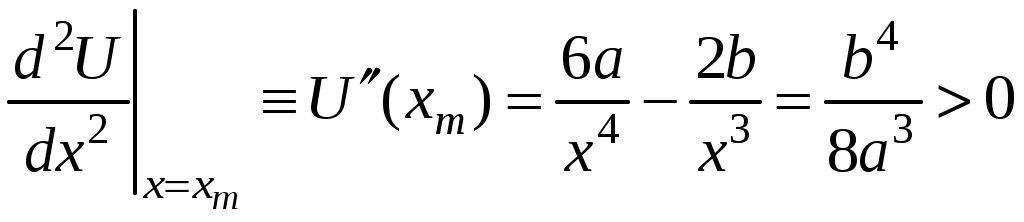 Таким образом, вычисленная точка определяет минимум потенциальной энергии, построим график Разложим 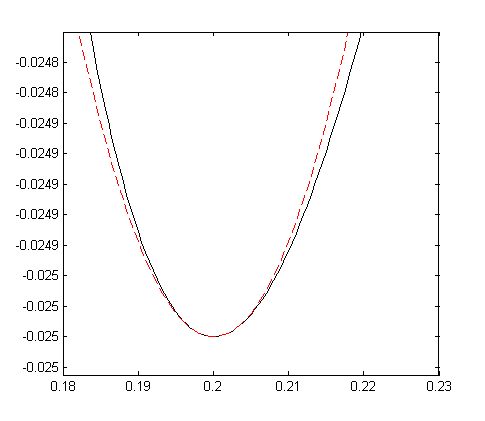 Рис.6.1. Потенциальная энергия частицы: Найдем уравнение движения маятника, для этого запишем уравнение Ньютона 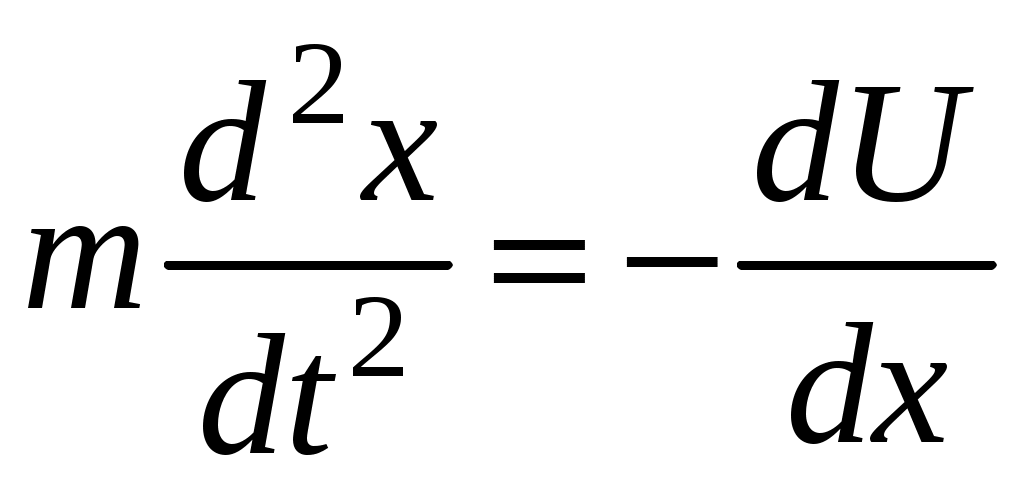 или или 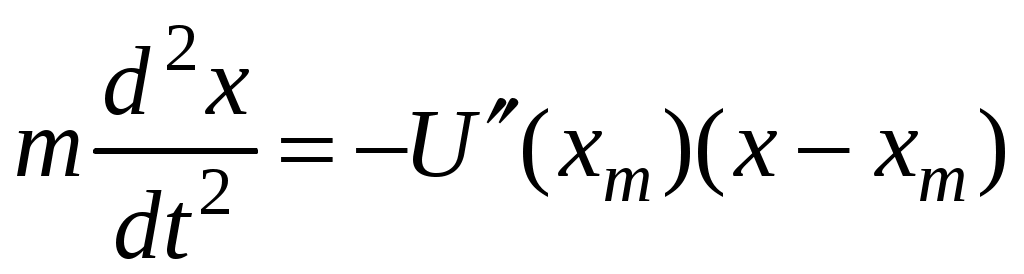 Перейдем к переменной 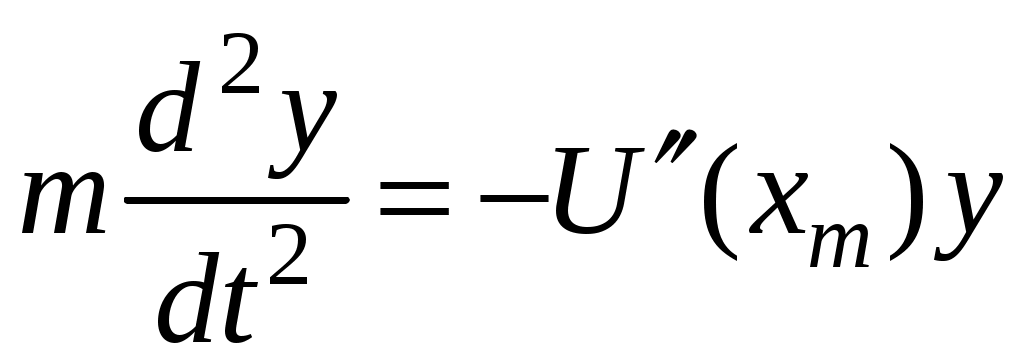 или или 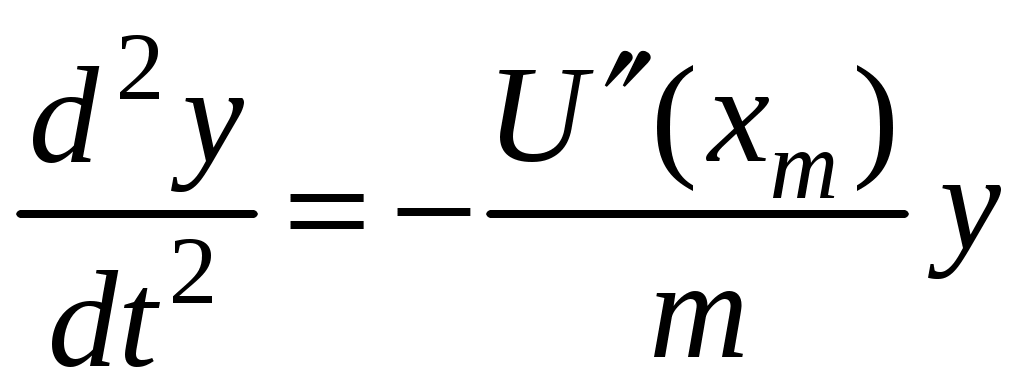 Тогда частота малых колебаний равна 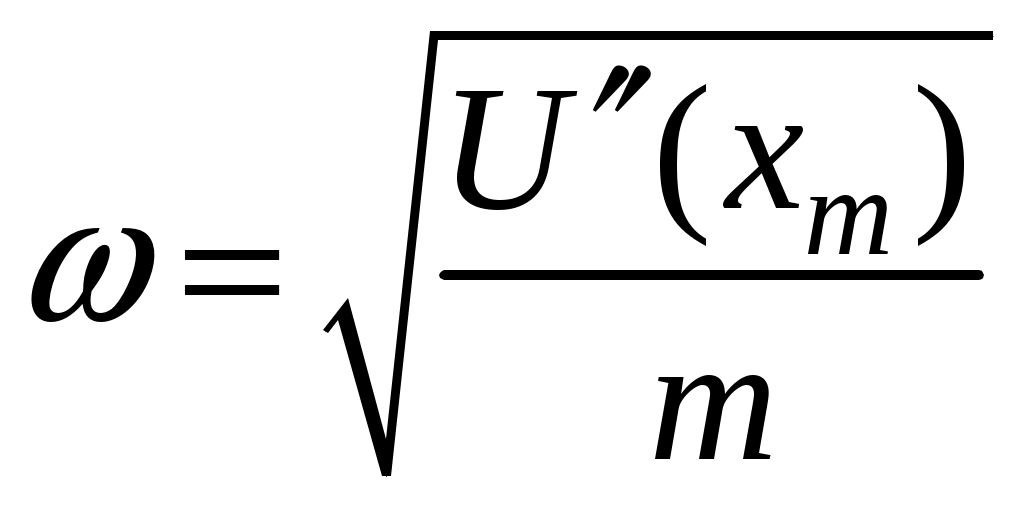 или или 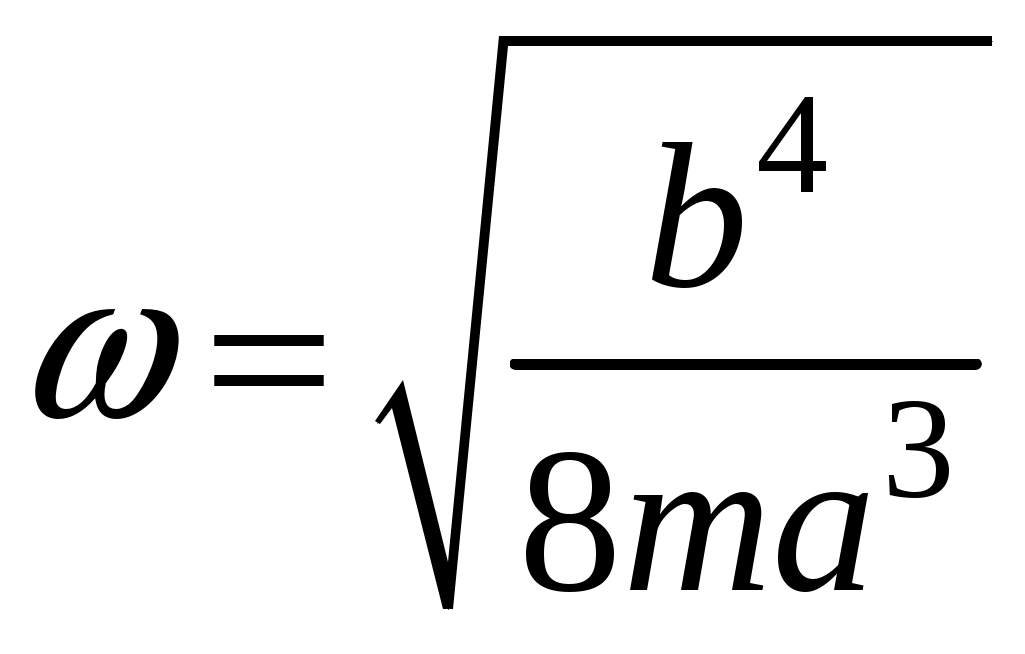 , , а период малых колебаний равен Чтобы построить график зависимости Тогда колебания тела описываются такой системой уравнений 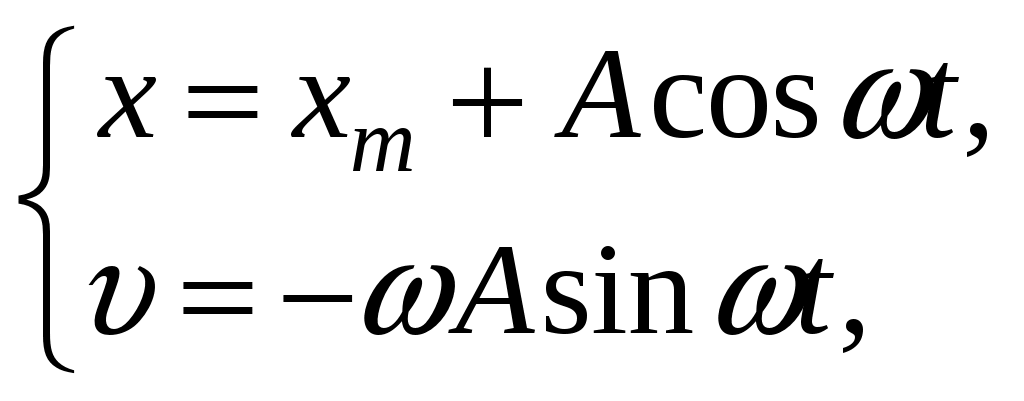 где Составим программу (Python). # Фазовая траектория частицы import math as mt import matplotlib.pyplot as plt a=0.001; b=0.01; m=0.2; x1=0.21; xm=2.*a/b; A=x1-xm; w=mt.sqrt(b**4/(8.*m*a**3)); T=2.*mt.pi/w; tmin=0.0; tmax=2.*T; NT=500; dt=(tmax-tmin)/NT; ti=[]; X=[]; V=[]; ti.append(tmin); X.append(x1); V.append(0.); for i in range(NT): t1=tmin+i*dt;ti.append(t1); X.append(xm+A*mt.cos(w*t1)); V.append(A*w*mt.sin(w*t1)); plt.plot(X,V,'k-') plt.grid(True) plt.xlabel('$x$',fontsize=16) plt.ylabel('$v$',fontsize=16) plt.show() По результатам расчета построим фазовый портрет движения тела 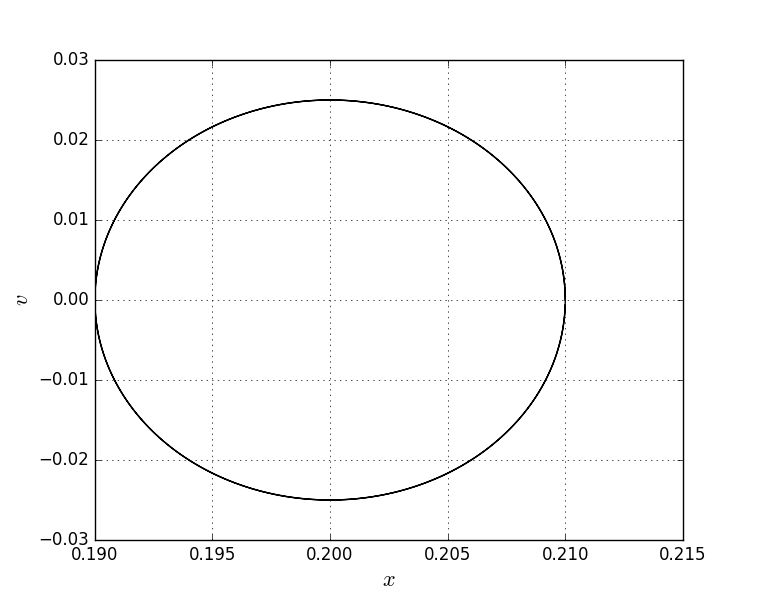 Рис.6.2. Фазовый портрет движения частицы. В начальный момент времени тело находится в крайнем правом положении, затем начинает смещаться влево по часовой стрелке по эллиптической траектории, как показано на рис.6.2, делая полный оборот за 2.51 с. Ответ: 6.1. Тело совершает колебания по закону 6.2. Тело совершает колебания по закону 6.3. Однородный диск массы 3 кг и радиуса 20 см скреплен в центре диска с тонким стержнем так, что стержень перпендикулярен плоскости диска. Другой конец стержня закреплен жестко и неподвижно. Коэффициент кручения стержня (отношение приложенного вращающего момента к углу закручивания) равен 6.00 Н·м/рад. Определить: а) частоту малых крутильных колебаний; б) амплитуду и начальную фазу колебаний, если в начальный момент времени угол 6.4. Материальная точка совершает колебания по закону синуса с амплитудой 10 см, частотой 2 Гц и начальной фазой 30 градусов. Полная энергия колеблющейся точки 0.077 Дж. Через какой промежуток времени от начала движения кинетическая энергия станет равной потенциальной? Построить график зависимости 6.5. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 6.6. Частица совершает гармонические колебания вдоль оси х около положения равновесия х=0 с частотой 4.00 с-1. В некоторый момент времени координата частицы равна 25 см и ее скорость 100 см/с. Найти координату и скорость частицы через 2.4 с после этого момента времени. Построить график зависимости 6.7. Определите амплитуду гармонических колебаний материальной точки, если полная энергия колеблющейся точки 0.04 Дж, а максимальная сила, действующая на точку, равна 2 Н. 6.8. Частица массы 0.2 кг находится в одномерном силовом поле, где ее потенциальная энергия зависит от координаты 6.9. На доске лежит груз массой 10 кг. Доска совершает гармонические колебания по закону косинуса в вертикальном направлении с периодом 0.5 с и амплитудой 2 см. Определите величину давления 6.10. Найти период малых поперечных колебаний шарика массы 40 г, укрепленного на середине натянутой струны длины 1 м. Силу натяжения струны считать постоянной и равной 10 Н. Массой струны и силами тяжести пренебречь. Построить график зависимости 7.Затухающие колебания Пример 7.1. Горизонтальное колебательное движение бруска при наличии сухого трения. Пружинный маятник представляет собой брусок массой Для численных расчетов принять Математическая модель 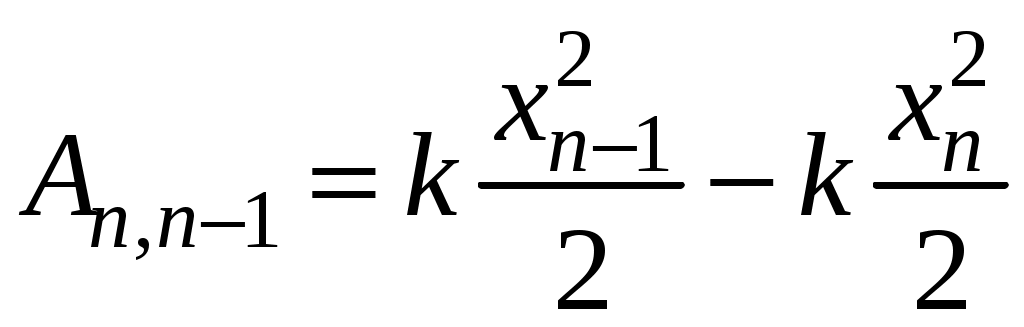 (7.3) (7.3)Знак минус в (7.2) связан с тем, что сила трения направлена против смещения бруска, Решение Процесс движения бруска показан на рис.1 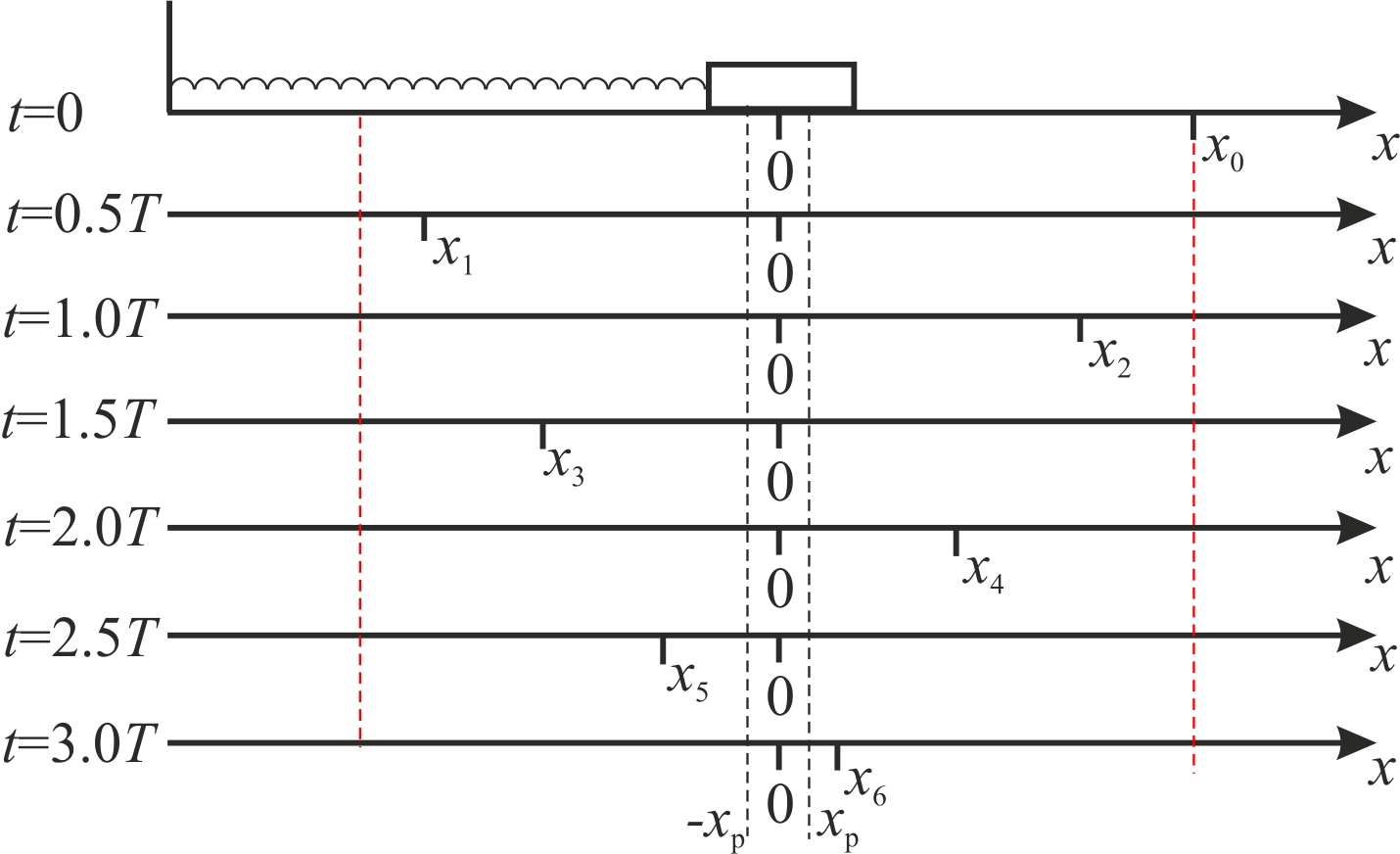 Рис.7.1. Координатно-временная развертка крайних положений бруска Решение Из (7.2) и (7.3) следует 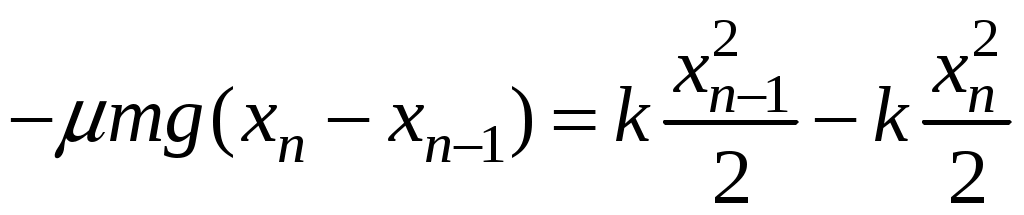 (7.4) (7.4)Определим область застоя Из (4) координаты крайних точек остановки равны Колебания продолжаются до тех пор, пока 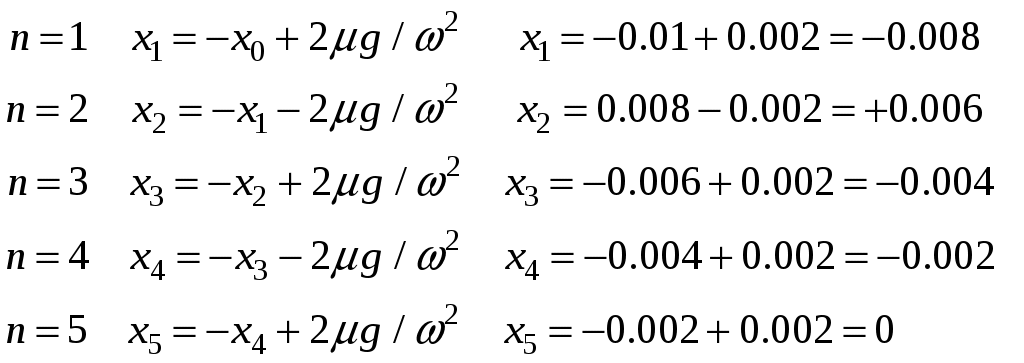 Время движения равно Для проверки проделаем численный расчет движения бруска на основе модели (7.1), проектируем на горизонтальную ось, получаем уравнение движения Движение справа — налево Движение слева — налево На рис.7.2 представлен результат численного расчета данной модели (текст программы приведен в Приложении) 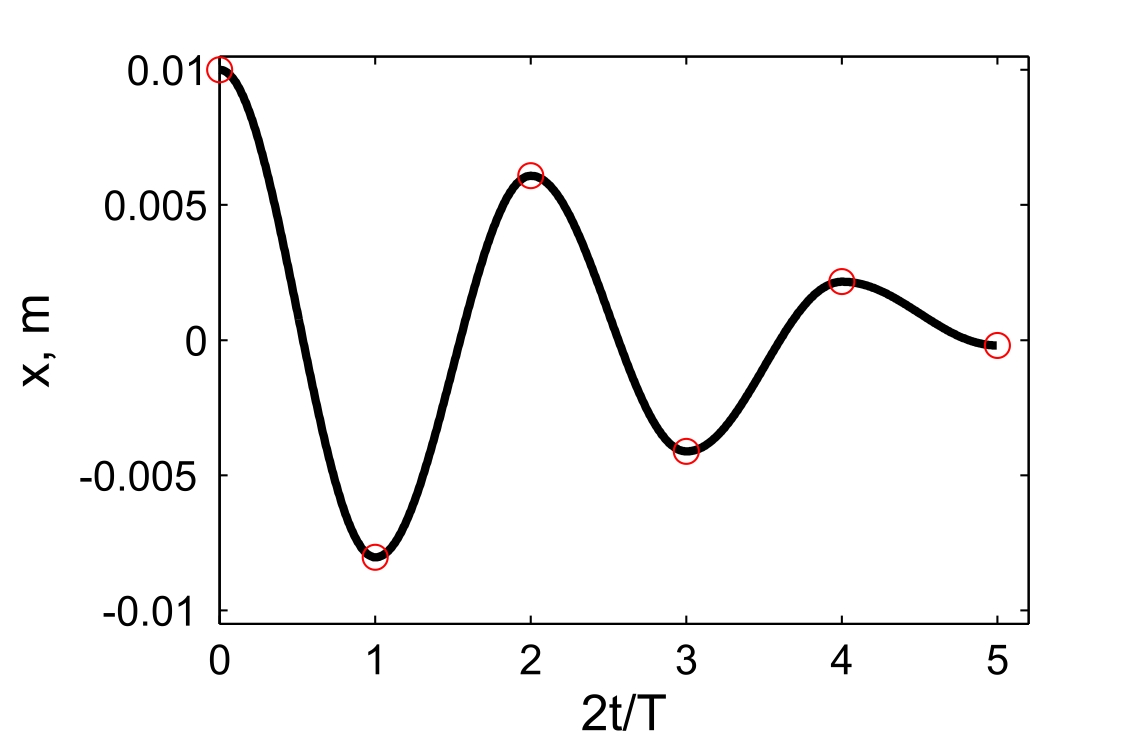 Рис. 7.2. График колебаний бруска, рассчитанный по модели (7), (8). Кружки отмечают крайние положения Несмотря на совпадения крайних положений бруска с положениями бруска, рассчитанными по модели (7.7) и (7.8), мы получили правдоподобный результат, поскольку в решении мы не учли область застоя около положения равновесия. График скорректированного решения приведен на рис.7.3.  Рис. 7.3. График колебаний бруска, рассчитанный по модели (7), (8) с учетом области застоя. Кружки отмечают скорректированные крайние положения Таким образом, колебания бруска затухают слабее, поскольку в области застоя брусок движется равномерно. Получается парадокс, шероховатость горизонтальной плоскости везде одинакова, а в области застоя работу силы трения не учитываем. Ответ: Маятник совершил 2.25 колебания в течение 1.57 секунд. 7.1. Груз массой 0.5 кг подвешен к пружине, жесткость которой 32 Н/м, и совершает затухающие колебания. Определите период затухающих колебаний, если за время двух колебаний амплитуда уменьшилась в 3 раза. Построить график зависимости 7.2. Маятник длиной l = 5 м совершает малые колебания, так что амплитуда их уменьшилась в два раза за 100 периодов. Найдите добротность Q колебаний, логарифмический декремент λ и коэффициент затухания γ. Построить график зависимости 7.3. Затухающие колебания частицы были возбуждены путем ее смещения из положения равновесия на расстояние 1 см. Логарифмический декремент затухания 0.0100. При столь слабом затухании можно с большой точностью считать, что максимальные отклонения от положения равновесия достигаются в моменты времени равные 7.4.Чему равен логарифмический декремент затухания колебаний и добротность системы, если амплитуда затухающих колебаний уменьшилась в 10 раз за 50 колебаний? Построить график зависимости 7.5. К пружине подвесили грузик, и она растянулась на 1 см. С каким периодом будет колебаться грузик в вертикальном направлении? Логарифмический декремент затухания равен 4. Построить график зависимости 7.6. Частицу сместили из положения равновесия на расстояние 1 см и предоставили самой себе. Какой путь пройдет, колеблясь, эта частица до полной остановки, если логарифмический декремент затухания равен 0.020? Построить график зависимости 7.7. Энергия затухающих колебаний маятника, происходящих в некоторой среде, за время 2 мин уменьшилась в 100 раз. Определите коэффициент сопротивления, если масса маятника 100 г. Построить график зависимости 7.8. На колеблющийся шарик массы m на пружинке жесткостью k действует сила трения 7.9. Найти добротность математического маятника длины 0.5 м, если за 5.2 минуты его полная энергия уменьшилась в 7.10. Измерены три последовательных амплитуды затухающих колебаний пружинного маятника 8.6, -4.1, 4.3 мм. Каково среднее положение осциллятора и логарифмический декремент затухания колебаний λ? 8. Вынужденные колебания. Резонанс 8.1. Найдите усредненные значения кинетической и потенциальной энергии гармонического осциллятора под действием внешней гармонической силы в режиме установившихся колебаний. Как они соотносятся между собой при различных значениях частоты вынуждающих колебаний? 8.2. При какой скорости поезда рессоры его вагонов будут особенно сильно колебаться под действием толчков колес о стыки рельс, если длина рельс 12.5 м, нагрузка на рессору 5.5 тонн и если рессора прогибается на 16 мм при нагрузке в 1 тонну? Построить амплитудно-частотную характеристику. 8.3. Человек массой 60 кг качается на качелях. Его движения описывается уравнением 8.4. Амплитуды смещений вынужденных гармонических колебаний при частотах 500 Гц и 600 Гц равны между собой. Найдите частоту, при которой амплитуда смещений максимальна 8.5. Амплитуды скорости вынужденных гармонических колебаний при частотах вынуждающей силы 500 Гц и 600 Гц равны между собой. Принимая, что амплитуда вынуждающей силы в обоих случаях одна и та же, найдите частоту, соответствующую резонансу скорости. 8.6. Оценить, через сколько времени установятся колебания в системе с добротностью 8.7. Найти добротность осциллятора, у которого отношение резонансной частоты к частоте затухающих колебаний равно 0.97. 8.8. При изменении частоты 8.9. Под действием момента сил 8.10. Шарик массы 50 г подвешен на пружинке жесткостью 20 Н/м. Под действием вынуждающей вертикальной гармонической силы с частотой 25 рад/с шарик совершает установившиеся колебания. При этом смещение шарика отстает по фазе от вынуждающей силы на 8.11. Через речку переброшена доска. Когда мальчик стоял неподвижно, она прогибалась на 10 см. Когда же он пошел со скоростью 3.6 км/час, то доска так раскачалась, что он упал в воду. Каков размер шага мальчика? 9. Релятивистская механика 9.1. Стержень движется в продольном направлении с постоянной скоростью относительно инерциальной К-системы отсчета. При каком значении скорости длина стержня в этой ИСО будет на 50% меньше его собственной длины? 9.2. Имеется прямоугольный треугольник, у которого катет 9.3. Найти собственную длину стержня, если в К-системе отсчета его скорость 0.5с, длина 1.00 м и угол между стержнем и направлением движения 45 градусов. 9.4. С какой скоростью двигались в К-системе отсчета часы, если за 5 с (в системе К) они отстали от часов этой системы на 0.1 с? 9.5. Собственное время некоторой нестабильной частицы 10 нс. Какой путь пролетит эта частица до распада в лабораторной системе отсчета, где её время жизни 20 нс? 9.6. В плоскости 9.7. Две частицы движутся навстречу друг другу со скоростями 0.5с и 0.75с по отношению к лабораторной системе отсчета. Найти: а) скорость, с которой уменьшается расстояние между частицами в лабораторной системе отсчета; б) относительную скорость частиц. 9.8. Найти скорость, при которой релятивистский импульс в 1.4 раза превышает её ньютоновский импульс. 9.9. Какую работу надо совершить, чтобы сообщить электрону скорость, равную а) 0.5с, б) 0.99с? 9.10. Найти скорость частицы, кинетическая энергия которой 500 МэВ и импульс 865 МэВ/с, где с- скорость света. |
