Контрольная. Сопр.Мат.. Контрольная (СОПР.МАТ). Рассечем стержень произвольным сечением 1 Верхнюю часть отбросим
 Скачать 64.79 Kb. Скачать 64.79 Kb.
|
|
Задача №1 В соответствии с заданной схемой нагружения стержня определить внутренние силы; построить эпюры распределения этих сил по длине стержня; построить эпюры распределения нормальных напряжений по длине стержня, определив их значения для характерных точек по длине стержня. При этом учитывая внешние нагрузки, действующие на стержень и собственный вес стержня. Значение веса единицы объема принять равным 77 кН/м 3. Дано: А = 0,0012 м2 а = 3,0 м b = 3,0 м с = 3,0 м F =1,0 м  = 77 кН/м3 = 77 кН/м3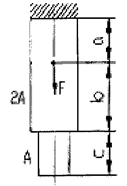 Для построения эпюр внутренних сил, используем метод сечений. Грани-цами являются концевые сечения, места изменения поперечного сечения и точки приложения сил. Рассечем стержень произвольным сечением 1-1. Верхнюю часть отбросим. Рассмотрим 1 (первый) участок (1-1). Участок 1 – 1. Для определения силы N1 составим уравнение по оси Y: 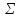 y = 0; y = 0;N1 - A  · x1 = 0; · x1 = 0;N1 = A  · x1; · x1;0 < х1 < с 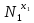 =0= A =0= A 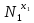 =с= A =с= A · c = 0,0012 · 77 · 3 = 0,2772 кН · c = 0,0012 · 77 · 3 = 0,2772 кНРассмотрим 2 участок стержня, рассеченный произвольным сечением 2-2. Верхнюю часть отбрасываем. Участок 2 – 2. Определяем силы N2 и составим уравнение по оси Y: 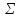 y = 0; y = 0;N2 - F - A  · c - 2A · c - 2A · x2 = 0 · x2 = 0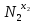 =0= F+ A =0= F+ A · с -2 A · с -2 A · x2 = 0 · x2 = 00 < х2 < b 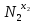 =0= F+2A =0= F+2A · x2 = 1+2 · 0,0012 · 3 = · x2 = 1+2 · 0,0012 · 3 =  1,0072 кН 1,0072 кН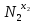 =b= F+ A =b= F+ A · с -2 A · с -2 A · b = 0,8316 кН · b = 0,8316 кНРассмотрим 3 участок стержня, рассеченный произвольным сечением 3 - 3. Участок 3 – 3. Определяем силы N3 и составим уравнение по оси Y: 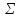 y = 0; y = 0;N3- F - A  · c - 2A · c - 2A · b -A · b -A · x3 = 0 · x3 = 0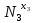 =0= F+ A =0= F+ A · с + 2 A · с + 2 A · b + A · b + A · x3 = 0 · x3 = 00 < х2 < a 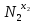 =0= F+ A =0= F+ A · с + 2 A · с + 2 A · b = 0,8316 кН · b = 0,8316 кН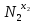 =a= F+ A =a= F+ A · с + 2 A · с + 2 A · b + A · b + A · a = · a = = 1,5544 кН Определяем напряжения 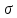 на участках стержня: на участках стержня: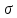 1 = 0 мПа; 1 = 0 мПа;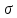 2 = N1/A =0,2772 / 0,0012 = 231 мПа; 2 = N1/A =0,2772 / 0,0012 = 231 мПа;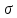 3 = N2/A = 0,8318 / 0,0012 = 693 мПа; 3 = N2/A = 0,8318 / 0,0012 = 693 мПа;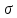 4 = N2/2A = 0,8316 / 2 · 0,0012 = 346,5 мПа; 4 = N2/2A = 0,8316 / 2 · 0,0012 = 346,5 мПа;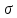 5 = N3/A = 1,5544 / 0,0012 = 1295 мПа. 5 = N3/A = 1,5544 / 0,0012 = 1295 мПа.Задача № 2 Исходя из условий прочности и жесткости, при растяжении, предложить рациональное сечение стержня нагруженного внешними силами если известны: Дано: F1 = 50 кН; с = 0,35 м; F2 = 20 кН; nр. = 2 F3 = 90 кН; nсж. = 1,5 a = 0,4 м; 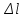 = 0,002 м; = 0,002 м;b = 0,8 м; 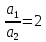 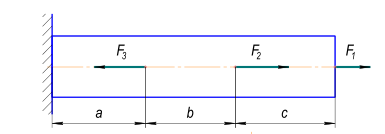 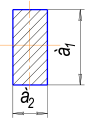 Стержень разделим на 3 в зависимости от изменения внешней нагрузки и площади поперечного сечения. Применим метод сечений и определим продольную силу на каждом участке. На участке 1: N1 = F1 = 50 кН ; На участке 2: N1 = F1 + F2 = 50 + 20 = 70 кН ; На участке 3: N1 = F1 + F2 – F3 = -20 кН ; Найдем напряжения на участках стержня. На участке 1: 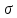 1 = 1 = 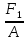 = = 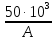 кПа кПаНа участке 2: 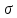 2 = 2 = 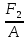 = = 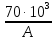 кПа кПаНа участке 3: 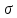 3 = 3 = 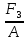 = = 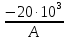 кПа кПаНаибольшее растягивающее напряжение на участке 2 - 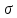 2 == 2 == 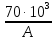 кПа, наибольшее сжимающее напряжение – на участке 3 - кПа, наибольшее сжимающее напряжение – на участке 3 - 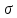 3 = 3 =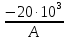 кПа. С учётов этих данных расчет произведем на самый нагруженный участок – на участок 2. Для этого используем условие прочности на растяжение данного участка: кПа. С учётов этих данных расчет произведем на самый нагруженный участок – на участок 2. Для этого используем условие прочности на растяжение данного участка: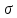 мах.р. = мах.р. = 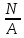 ≤ ≤ 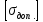 ; ; 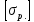 = = 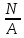 ; А = ; А = 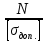 = =  где, 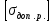 = 125 МПа для стали Ст3; = 125 МПа для стали Ст3;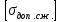 = 190 МПа для стали Ст3; = 190 МПа для стали Ст3;Напряжение на участке 1: 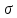 1 = 1 = 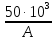 кПа. кПа.Тогда 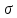 3 = 3 = 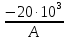 ≤ ≤ 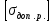 . .А ≤ 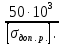 = = 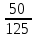 = 0,4 м2 = 0,4 м2 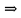 400 мм2. 400 мм2.Напряжение на участке 2: 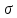 2 = 2 = 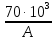 Па. Па.Тогда 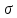 2 = 2 = 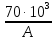 ≤ ≤ 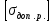 . .А ≤ 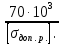 = = 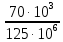 = 5,6 = 5,6 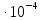 м2 м2 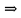 56 мм2. 56 мм2.Напряжение на участке 3: 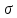 3 = 3 = 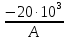 Па. Па.Тогда 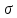 3 = 3 = 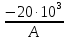 ≤ ≤ 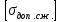 . .А ≤ 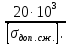 = = 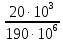 = 1,0525 ≈ 1 = 1,0525 ≈ 1 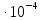 м2 м2 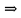 10 мм2. 10 мм2.Данные расчеты нам показывают, что 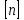 = = 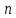 2 =1. По условию задачи nр.=2. Следовательно, применим формулу с применением коэффициента запаса прочности при растяжении: 2 =1. По условию задачи nр.=2. Следовательно, применим формулу с применением коэффициента запаса прочности при растяжении: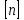 = = 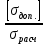 ; ;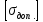 ≤ ≤ 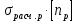 ; ; 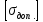 ≤ ≤ 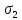 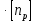 = 2 = 2  70 70  103 = 140 103 = 140  103 Па 103 Па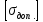 ≤ ≤ 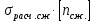 ; ; 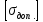 ≤ ≤ 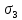 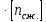 = 1,5 = 1,5  20 20  103 = 103 = = 30  103 Па 103 ПаЗначение запаса прочности примем по наибольшему значению нагрузок - Проверим условие прочности: 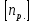 ≥ nрасч. = ≥ nрасч. = 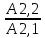 = = 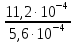 = 2. = 2. Условие запаса прочности выполнено. Тогда, Тогда 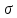 2 = 2 = 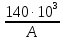 ≤ ≤ 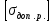 . .А ≤ 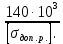 = = 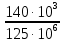 = 11,2 = 11,2 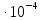 м2 м2 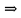 112 мм2. 112 мм2.Необходимую площадь сечения примем из условия прочности при растяжении: А ≤ 11,2 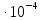 м2 м2 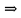 112 мм2. 112 мм2.При заданном соотношении а1 / а2= 2 площадь поперечного сечения можно записать, как А = а1  а2 = а2 = 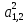 . Размеры поперечного сечения будут равны: . Размеры поперечного сечения будут равны:а2 = 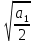 = = 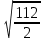 = 7,48 мм; = 7,48 мм;а1 = 2а2 = 2  7,48 = 14,96 мм. 7,48 = 14,96 мм.Находим площадь поперечного сечения из условия жесткости При расчете на жесткость следует учитывать, что перемещение точек будет равно сумме деформаций всех участков стержня. Величину абсолютной деформаций для каждого участка найдем по формуле: 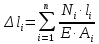 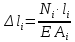 или или 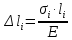 . .где, Ni – продольная сила, на i-ом участке стержня; li - длина, на i-ом участке стержня; Аi – площадь поперечного сечения, на i-ом участке стержня; Е – модуль упругости первого рода. Для стали Ст3: Е=2,1  105 105На участке 1: 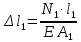 = = 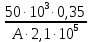 = = 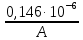 м. м.На участке 2: 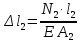 = = 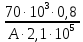 = = 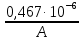 м. м.На участке 3: 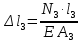 = = 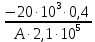 = = 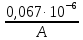 м. м.Абсолютная деформация всего стержня: 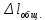 = = 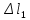 + + 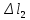 + + 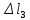 = = = = 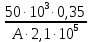 + + 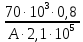 + + 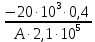 = = 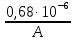 м. м.Из условия жёсткости: ∆l≤ [∆l], [∆l] =2 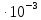 м, найдем м, найдем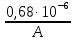 ≤ 2 ≤ 2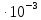 , откуда , откудаА ≥ 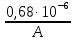 = = 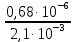 = 3,2 · 10-4 м2 = 3,2 · 10-4 м2 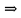 32 мм2 32 мм2Учтём значение запаса прочности при сжатии: Запас прочности при сжатии [nсж.] = 1,5; Применим для расчета формулу: 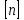 = = 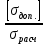 . .А ≥ [А] = 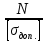 . .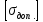 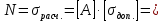 3,2 · 10-3·190 ·106 = 60,8 · 103 Па 3,2 · 10-3·190 ·106 = 60,8 · 103 Па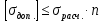 ; ; 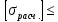 60,8 · 103 · 1,5 = 90,75 · 103 Па 60,8 · 103 · 1,5 = 90,75 · 103 ПаN ≤ [N] = A · 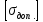 A = 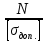 ; A = ; A =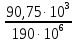 = 4,78 · 103 м2 = 4,78 · 103 м2 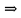 48 мм2. 48 мм2.Размеры поперечного сечения будут равны: а2 = 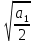 = = 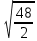 = 4,9 мм; = 4,9 мм;а1 = 2а2 = 2  7,48 = 9,8 мм. 7,48 = 9,8 мм.Сопоставляя результаты расчета на прочность и жесткость, принимаем большее значение площади поперечного сечения А = 112 мм2. Задача №3 Для заданной схемы двухопорной балки требуется: 1. Определить опорные реакции и произвести их проверку. 2. Написать аналитические выражения изгибающего момента М. 3. Построить эпюры изгибающих моментов М. На эпюре указать численные значения ординат для характерных сечений. 4. По максимальному изгибающему моменту подобрать стальную балку двутаврового поперечного сечения при допускаемом напряжении [σ]=160 МПа. 5. Принять длину одного пролета балки l = 1 м. Д 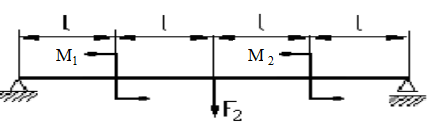 ано: ано:М1 = 3 кН·м М2 = 1,5 кН·м F2 = 3,5 кН [σ]=160 Мпа Из условия равновесия балки, взяв сумму моментов относительно точек А и Б, находим реакции в опорах: ∑MA=0, M1 + M2 – F2 · 2l + RB · 4l = 0 RB = 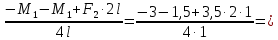 0,625 Кн 0,625 Кн∑MБ=0, -RA · 4l+M1+ M2+ F2 · 2l = 0 RА = 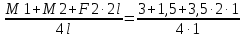 = 2,875 Кн = 2,875 КнПроверка ∑y=0; -RA – F2 + RБ =2,875-3,5+0,625 = 0, реакции найдены верно. Аналитические выражения изгибающих моментов М: Ⅰ участок: 0 ≤ Z1 ≤ l; l = 1 м. MⅠ = KA · Z1. При Z1 = 0; MⅠ = 0; при Z1 = 1м; MⅠ = 2,875 · 1 =2,875 кН·м Ⅱ участок: l ≤ Z2 ≤ 2l; 1м ≤ Z2 ≤ 2м. MⅡ = RA · Z2 – М1. При Z2 = 1м; MⅡ = 2,875 · 1 – 3 = -0,125 кН·м При Z2 = 2м; MⅡ = 2,875 · 2 – 3 = 2,75 кН·м Ⅲ участок: 0 ≤ Z3 ≤ l; 0 ≤ Z3 ≤ 1м. MⅢ = RБ · Z3. При Z3 = 0; MⅢ = 0; Z3 = 1м; MⅢ = 0,625 · 1 = 0,625 кН·м Ⅳ участок: l ≤ Z4 ≤ 2l; 1м ≤ Z4 ≤ 2м MⅣ = RБ · Z4 +М2. При Z4 = 1м; MⅣ = 0,625 · 1 + 1,5 = 2,125 кН·м При Z4 = 2м; MⅣ = 0,625 · 2 + 1,5 = 2,75 кН·м Строим эпюру моментов. Построение эпюры поперечных сил: Ⅰ участок: 0 ≤ Z1 ≤ l; QⅠ = RA = 2,875 Кн –const; Ⅱ участок: l ≤ Z2 ≤ 2l; QⅡ = RA = 2,875 Кн –const; Ⅲ участок: 0 ≤ Z3 ≤ l; QⅢ = -RA= -0,625Кн –const; Ⅳ участок: l ≤ Z4 ≤ 2l; QⅣ = -RB = -0,625Кн –const; Определение размеров поперечного сечения балкиWz из условия прочности. По эпюре находим наибольший изгибающий момент, возникающий в сечениях балки Мz max = 3 кН·м. Используя условие прочности: Vmax ≤ [V] Определим момент сопротивления: Wz = 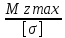 ≥ ≥ 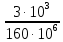 = 18,75 · 10-6 м3 = 18,75 см3. = 18,75 · 10-6 м3 = 18,75 см3.Определив Wz, находим размеры поперечного сечения. Для прямоугольного сечения: Wz = 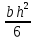 , ,где h = 2b. Следовательно, Wz = 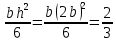 b3 = 18,75 см3. b3 = 18,75 см3.Отсюда b = 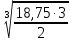 = 3 см. h = 2·b = 18 см. = 3 см. h = 2·b = 18 см.По таблице сортамента ( ГОСТ 8239-72 ) подбираем стальную балку двутаврового поперечного сечения ( Wz = 18,75 см3 ) - № 10 с моментом сопротивления Wz = 39,7 см3 и площадью сечения А = 12 см2. Проверяем выполнения условия прочности при подобранных размерах: 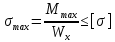 ; ;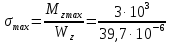 = 75,56 Мпа = 75,56 МпаСледовательно: 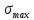 =75,56 Мпа ≤ [σ]=160 МПа. =75,56 Мпа ≤ [σ]=160 МПа.Условие прочности выполняется. |
