Рассмотрим равновесие тела, опирающегося на плоскость и подвешенного на нити. Заменим тело точкой
 Скачать 1.12 Mb. Скачать 1.12 Mb.
|
|
Задание 1 Определить графоаналитически и графически реакции плоскостей и стержней, удерживающих шар в равновесии (рисунок 1). 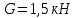 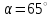 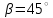 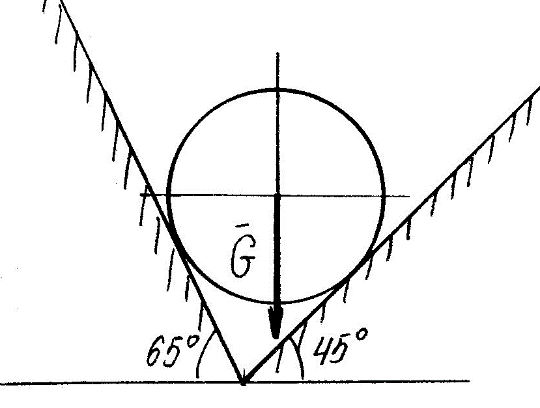 Рисунок 1 Заданная система Решение: Рассмотрим равновесие тела, опирающегося на плоскость и подвешенного на нити. Заменим тело точкой О, совпадающей с центром тяжести. Приложим к точке О активную силу, которой является собственный вес тела G. Направим ее вниз. Мысленно отбросим связи – плоскости. Заменим их действие на точку О реакциями связей. Реакция плоскости R1 проходит по нормали к плоскости в точке А, а реакция плоскости R2– по нормали к плоскости в точке B. Обе реакции и вес тела или линии их действия должны пересекаться в точке O (рисунок 2). 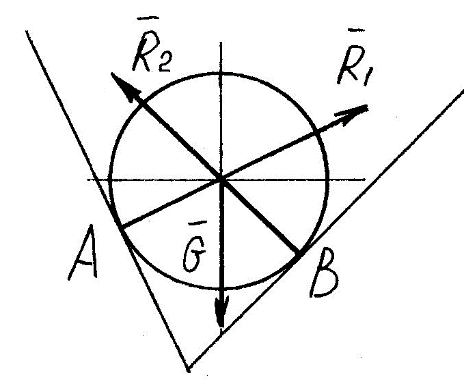 Рисунок 2 Замена сил реакциями Изобразим действующие силы в виде системы трех сходящихся сил. Выберем положение системы координат. Начало координат совмещаем с точкой О. Ось Х совмещаем с направлением линии действия реакции R1, а ось Y направим перпендикулярно оси X (рисунок 3). 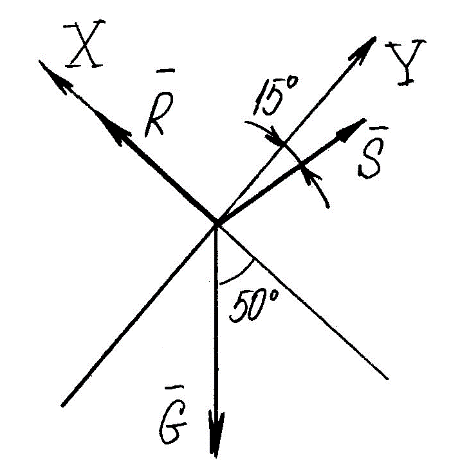 Рисунок 3 Равновесие шара Составим уравнения равновесия для системы сил. 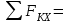 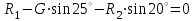 (1) (1)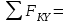 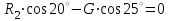 (2) (2)Из уравнения (2) найдём 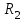 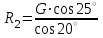 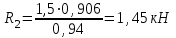 Из уравнения (1) найдём 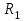 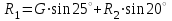 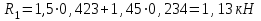 Для решения задачи графическим методом выбираем масштаб сил 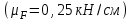 и строим замкнутый многоугольник сил (рисунок 4). Из произвольной точки О проводим прямую, параллельную вектору и строим замкнутый многоугольник сил (рисунок 4). Из произвольной точки О проводим прямую, параллельную вектору 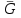 , и откладываем на этой прямой в выбранном масштабе вектор , и откладываем на этой прямой в выбранном масштабе вектор 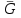 . Из конца вектора . Из конца вектора 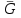 (точка А) проводим прямую, параллельную вектору (точка А) проводим прямую, параллельную вектору 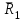 , а из точки О – прямую, параллельную вектору , а из точки О – прямую, параллельную вектору 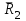 . Пересечение этих прямых дает точку B. Получили замкнутый треугольник сил ОАВ, стороны которого в выбранном масштабе изображают силы, сходящиеся в точке В. Величины сил . Пересечение этих прямых дает точку B. Получили замкнутый треугольник сил ОАВ, стороны которого в выбранном масштабе изображают силы, сходящиеся в точке В. Величины сил 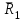 и и 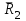 определим после измерения сторон АВ и ОВ треугольника ОАB. определим после измерения сторон АВ и ОВ треугольника ОАB.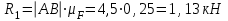 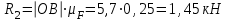 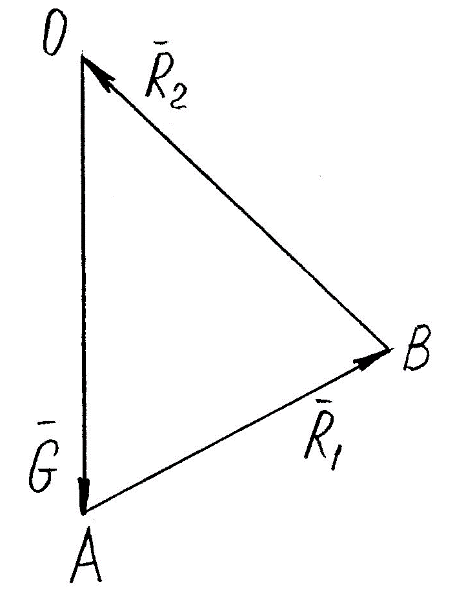 Рисунок 4 Графическое решение Задание 2 Для заданной балки определить опорные реакции в точках А и В (рисунок 5). 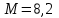 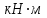 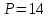 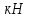 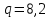 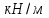 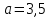 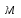 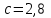 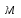 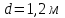 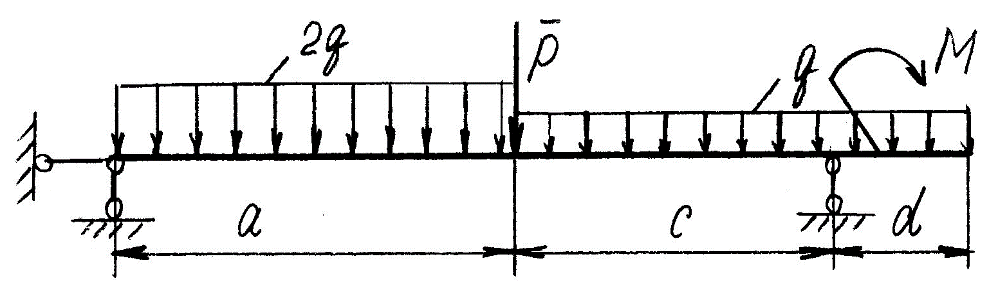 Рисунок 5 Заданная балка Решение: Заменяем равномерно распределённую нагрузку равнодействующей. На балку действуют нагрузки разной интенсивности, поэтому для каждой из них находим равнодействующую. 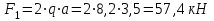 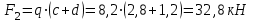 Рассмотрим равновесие балки. Проведём координатные оси XY и изобразим действующие на раму силы: пару сил с моментом М; силу 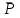 , равнодействующие , равнодействующие 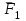 и и 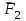 и реакции связей и реакции связей 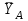 и и 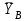 (рисунок 6). (рисунок 6).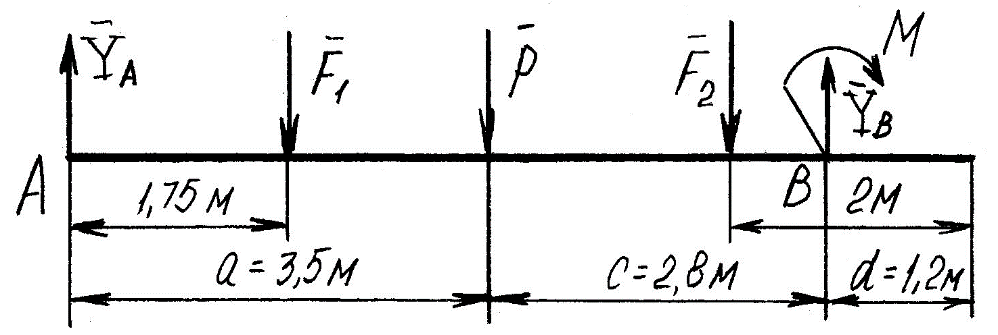 Рисунок 6 Балка, освобождённая от связей Составим уравнения равновесия 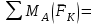 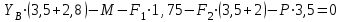 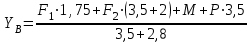 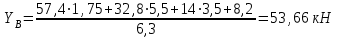 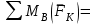 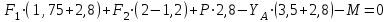 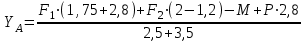 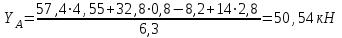 Сделаем проверку, составив уравнение равновесия 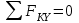 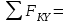 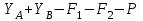 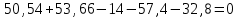 Равенство выполняется, следовательно, реакции опор определены верно. Задание 3 Определить опорные реакции пространственно нагруженного бруса (рисунок 6). 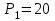 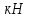 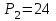 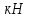 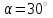 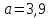 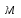 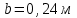 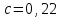 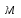 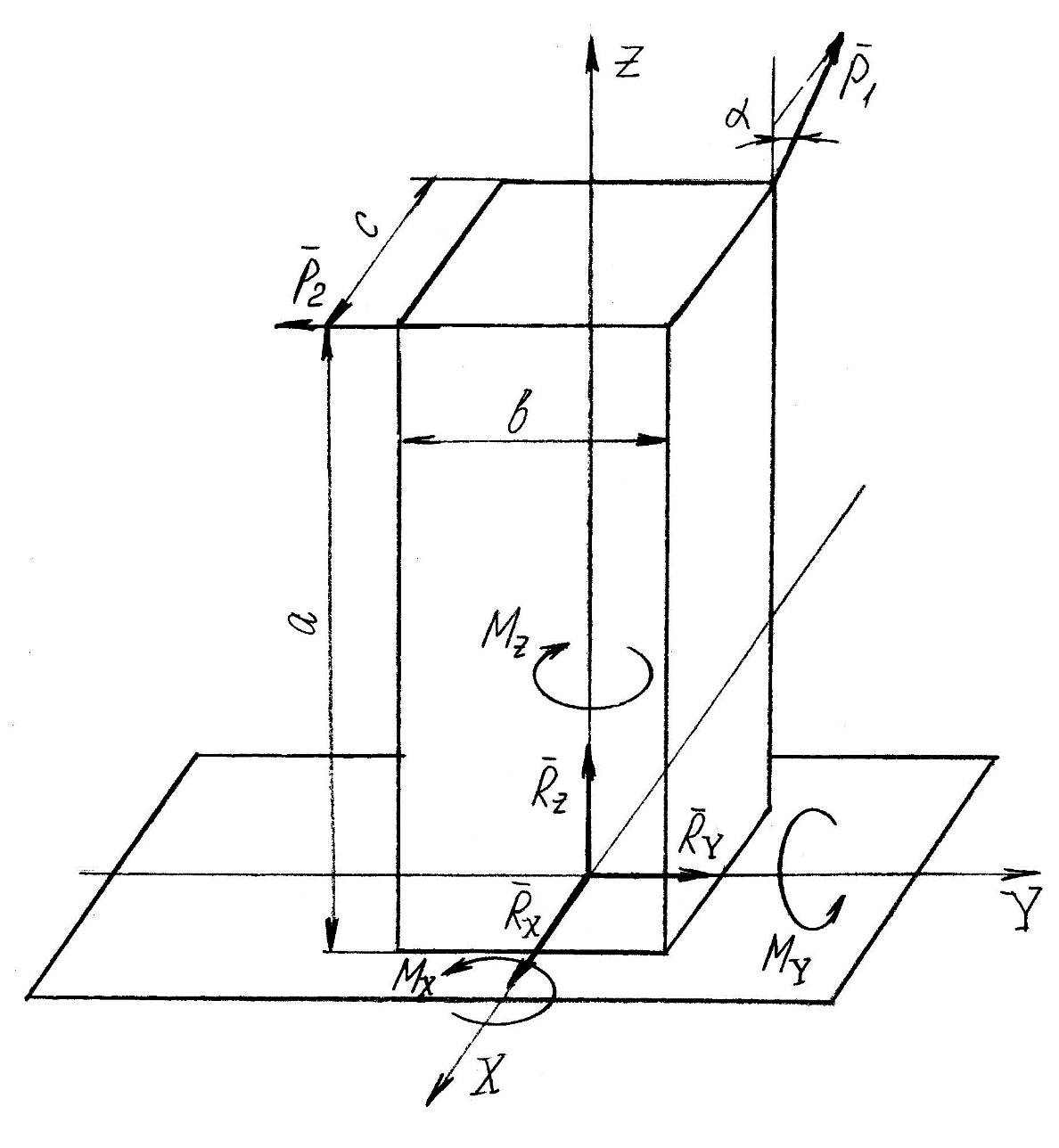 Рисунок 6 Заданная схема пространственно нагруженного бруса Решение: Освобождаем конструкцию от опор, заменив действие опор их реакциями. В заделке реакцию заменяем тремя составляющими – 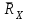 ; ; 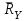 ; ; 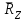 и тремя моментами – и тремя моментами – 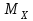 ; ; 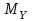 ; ; 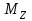 . .Имеем шусть неизвестных. Составим систему из шести уравнений равновесия сил и моментов. 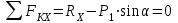 (1) (1)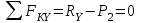 (2) (2)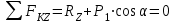 (3) (3) 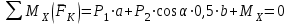 (4) (4) 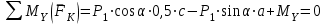 (5) (5) 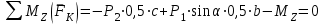 (6) (6) Из уравнения (1) найдём 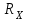 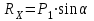 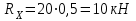 Из уравнения (2) найдём 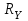 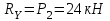 Из уравнения (3) найдём 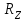 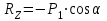 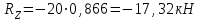 Из уравнения (4) найдём 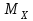 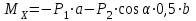 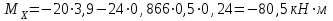 Из уравнения (5) найдём 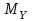 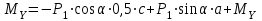 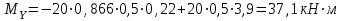 Из уравнения (6) найдём 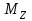  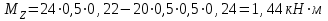 Задание 4 Построить эпюры продольных сил и нормальных напряжений по длине бруса. Определить перемещение свободного конца бруса. Двухступенчатый стальной брус (рисунок 7), нагружен силами 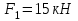 и и 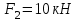 . . Площади поперечных сечений 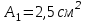 , , 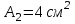 . . Модуль упругости 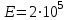 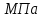 . .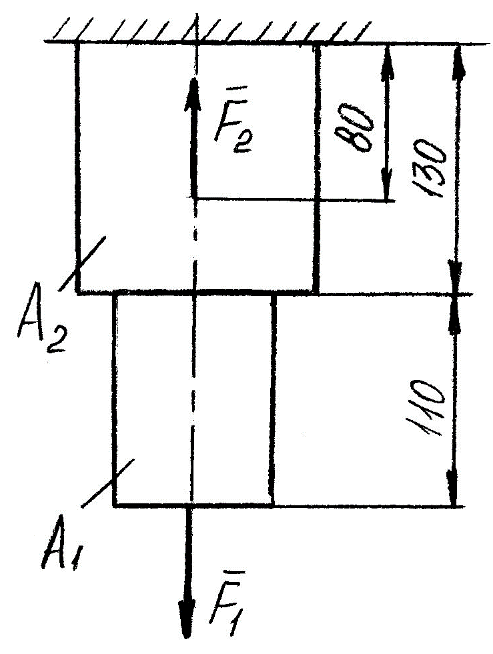 Рисунок 7 Заданный нагруженный брус Решение: Разбиваем брус на участки (I, II, III). Границами участков являются переходные по размерам поперечные сечения бруса и сечения, в которых приложена внешняя нагрузка – сосредоточенные силы 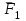 , , 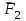 . Разбивка бруса на участки ведётся от свободного конца бруса, чтобы не определять величины реакций в заделке (рисунок 8, а). Продольные силы рассматриваются с учётом независимости их действия. . Разбивка бруса на участки ведётся от свободного конца бруса, чтобы не определять величины реакций в заделке (рисунок 8, а). Продольные силы рассматриваются с учётом независимости их действия.Для каждого участка, начиная с противоположного от защемления конца бруса, применяя метод сечений, определяем ординаты эпюры N на участках бруса (рисунок 8, б). Участок I Определяем силу 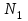 сопротивления первого участка растяжению сопротивления первого участка растяжению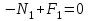 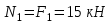 Участок II Определяем силу 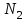 сопротивления второго участка растяжению сопротивления второго участка растяжению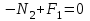 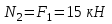 Участок III Определяем силу 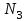 сопротивления второго участка сжатию сопротивления второго участка сжатию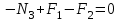 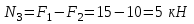 По результатам расчетов строим эпюры продольных сил (рисунок 8, в). Определяем нормальные напряжения на каждом участке. 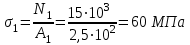 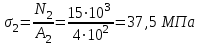 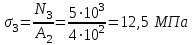 По результатам расчетов строим эпюры нормальных напряжений (рисунок 8, г). Определим абсолютные удлинения каждого участка. 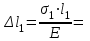 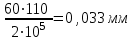 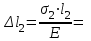 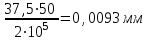 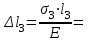 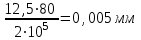 Перемещение свободного конца бруса 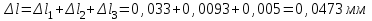 Брус растянут на 47,3 мкм. 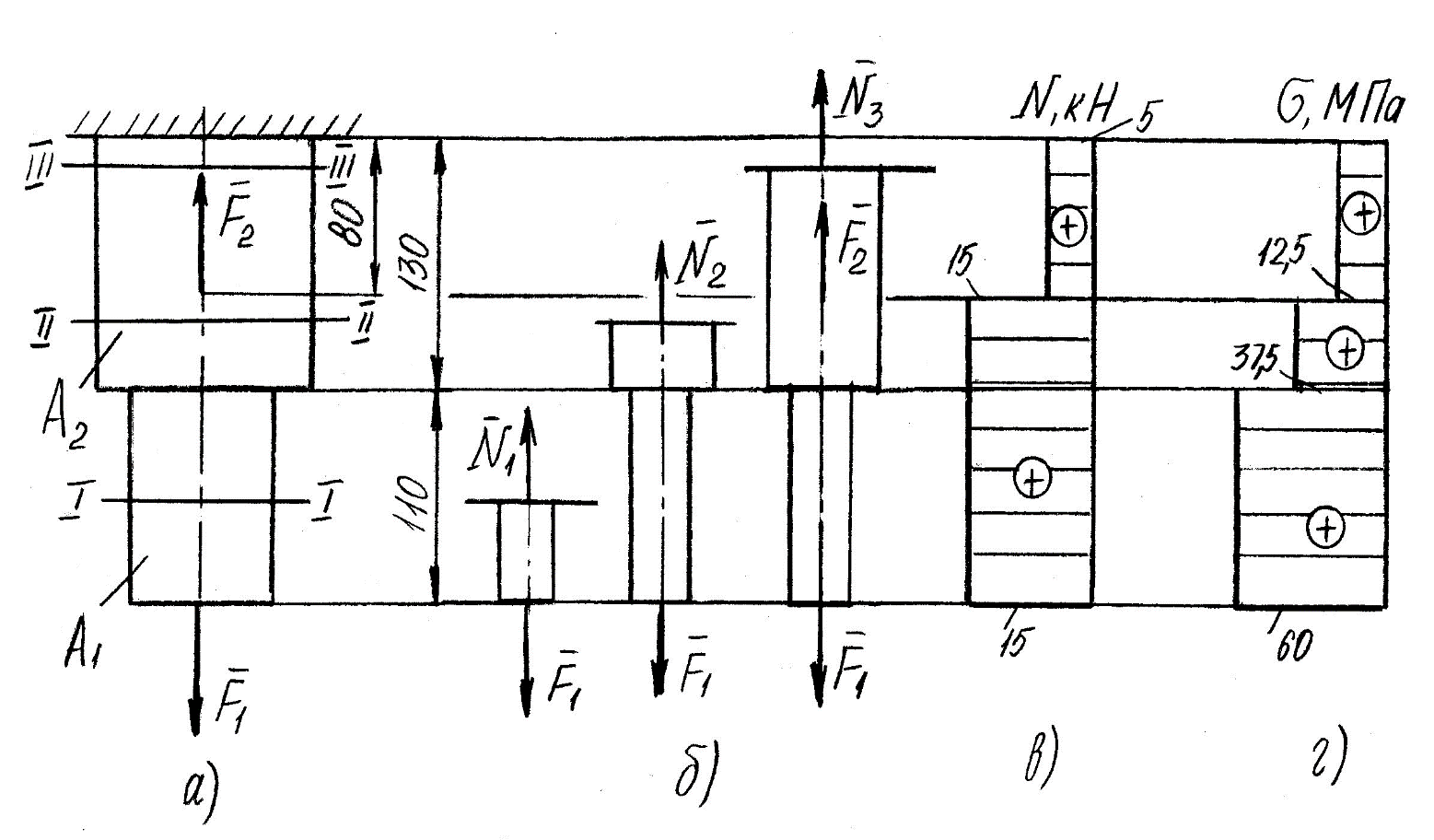 Рисунок 8 Построение эпюр Задание 5 Для стального вала круглого поперечного сечения (рисунок 9), вращающегося с угловой скоростью, определить значения внешних моментов соответствующих передаваемым мощностям, и уравновешивающий момент. Построить эпюру крутящих моментов по длине вала. Определить требуемый диаметр вала из расчетов на прочность и жесткость. 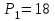       Допускаемое напряжение кручения  Допускаемый угол закручивания  Модуль упругости при сдвиге 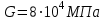 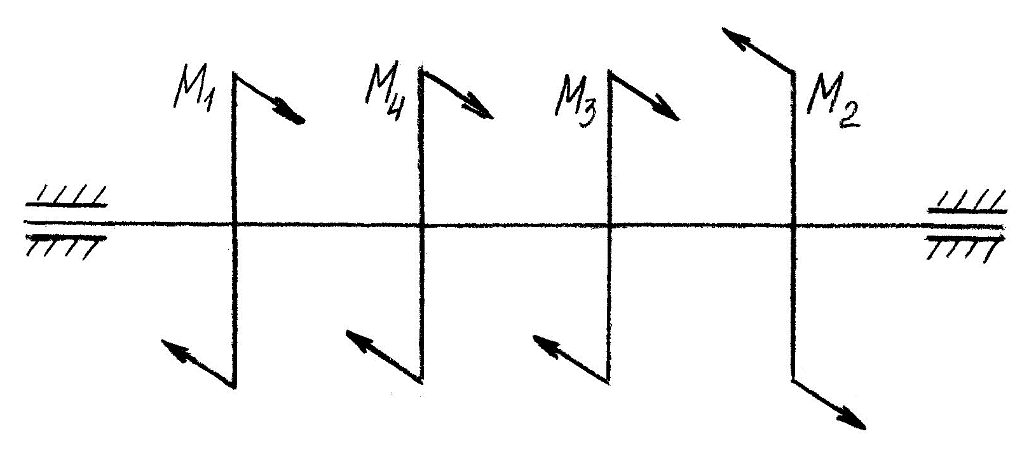 Рисунок 9 Заданная схема вала Решение: Определяем величины скручивающих моментов 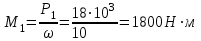 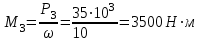 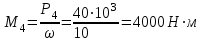 Найдем уравновешивающий момент 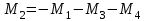 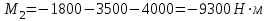 Разбиваем вал на участки (рисунок 10, а). Вал имеет три участка, границами которых являются сечения, в которых приложены внешние моменты. В пределах каждого участка значение крутящего момента сохраняется постоянным. Определяем крутящие моменты в поперечных сечениях вала с помощью метода сечений. Участок I 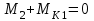 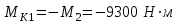 крутящий момент отрицательный Участок II 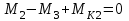 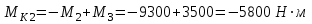 крутящий момент отрицаельный Участок III 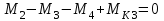 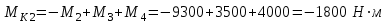 крутящий момент отрицательный Строим эпюру крутящих моментов (рисунок 10, б). 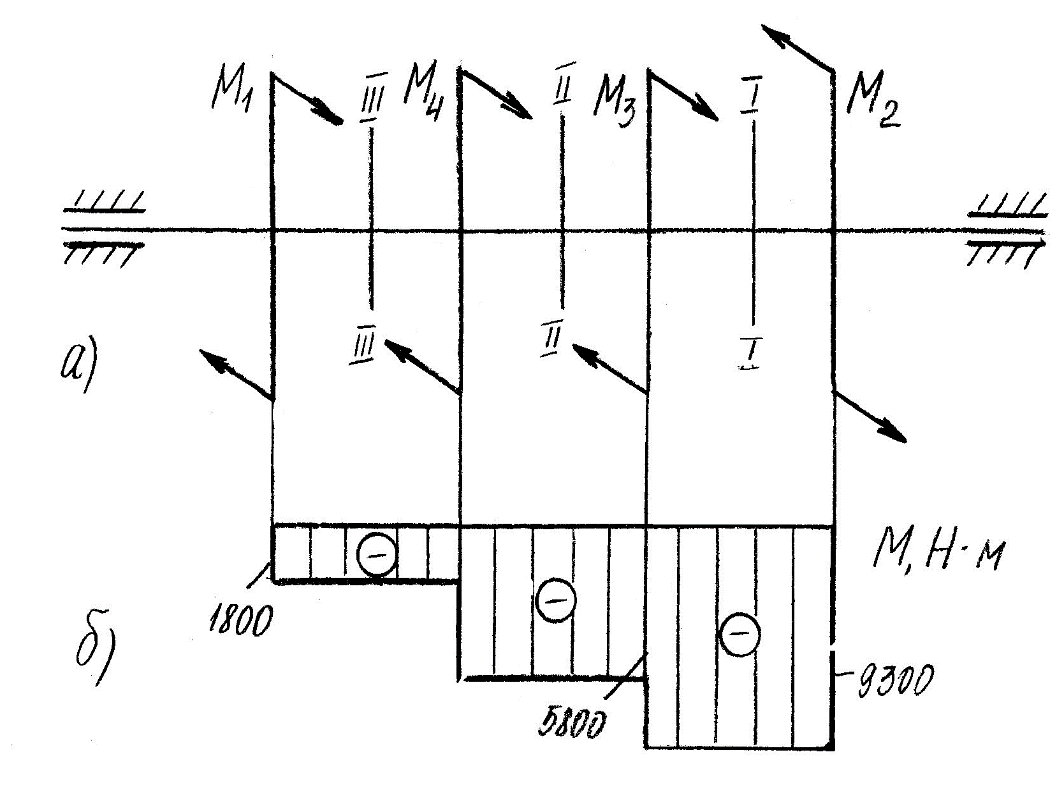 Рисунок 10 Построение эпюр Определяем диаметр вала для опасного участка, из условий прочности и жесткости. Опасным сечением является участок I. 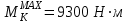 Определение диаметра вала из условия прочности Из условия прочности 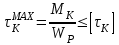 Найдем момент сопротивления при кручении 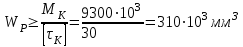 Учитывая, что момент сопротивления при кручении для круглого сечения определяется по формуле 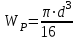 Определим диаметр вала 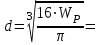 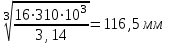 Определение диаметра вала из условия жесткости Из условия жесткости 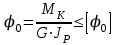 Определим полярный момент инерции сечения 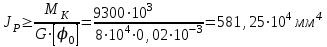 Учитывая, что момент сопротивления при кручении для круглого сечения определяется по формуле 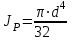 Найдем диаметр вала 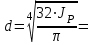 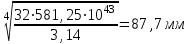 Для обеспечения прочности и жесткости одновременно из двух найденных диаметров выбираем большее. Требуемый диаметр вала получился больше из расчета на прочность, поэтому его принимаем как окончательный, округлив до ближайшего стандартного по ГОСТ6636-69. Окончательно принимаем 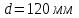 Задание 6 Для заданной двухопорной балки (рисунок 11) построить эпюры поперечных сил и изгибающих моментов. Подобрать поперечное сечение стальной балки в виде двух швеллеров и поперечное круглое сечение деревянной балки. 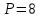 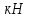 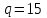 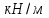 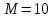 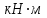 Допускаемое напряжение изгиба для стального проката 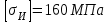 Допускаемое напряжение изгиба для деревянной балки 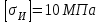 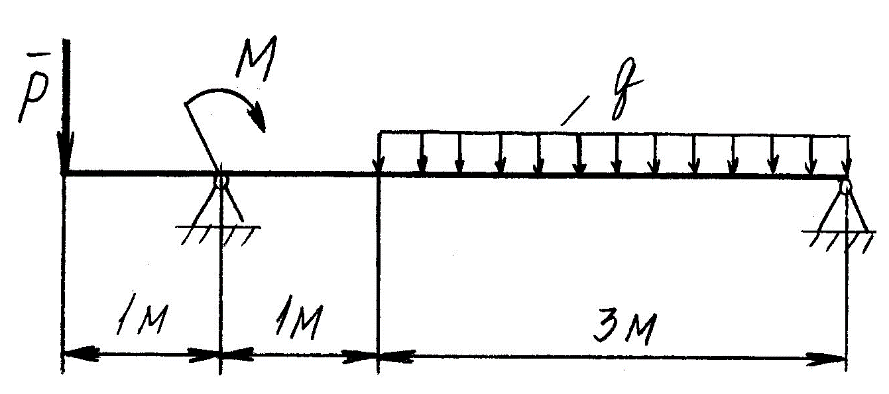 Рисунок 11 Заданная схема балки Решение: Обозначим реакции опор 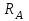 и и 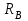 (рисунок 12, а) и определим их величину, используя уравнения равновесия для плоской системы сил (рисунок 12, а) и определим их величину, используя уравнения равновесия для плоской системы сил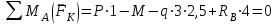 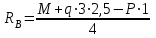 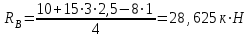 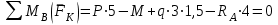 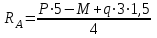 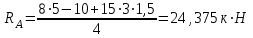 Проверим правильность определения реакций опор, составив уравнение проекций всех сил на ось 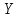 . .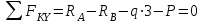 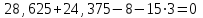 Равенство выполняется, следовательно, опоры определены верно. Разобьем балку на участки нагружения (рисунок 12, а). Границами участков являются сечения, в которых приложены внешние нагрузки. 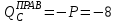 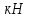 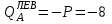 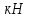 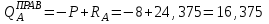 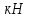 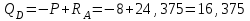 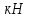   По полученным значениям строим эпюры поперечных сил (рисунок 12, б). 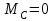 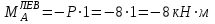 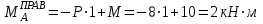 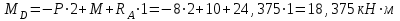 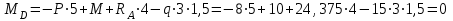 Для определения экстремального значения момента в сечении K, где 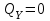 , определим длину KB. , определим длину KB. 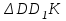 подобен подобен 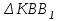 Отсюда 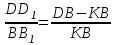 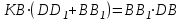 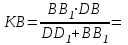 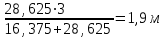 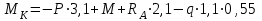 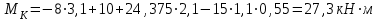 По полученным значениям строим эпюры изгибающих моментов (рисунок 12, в). 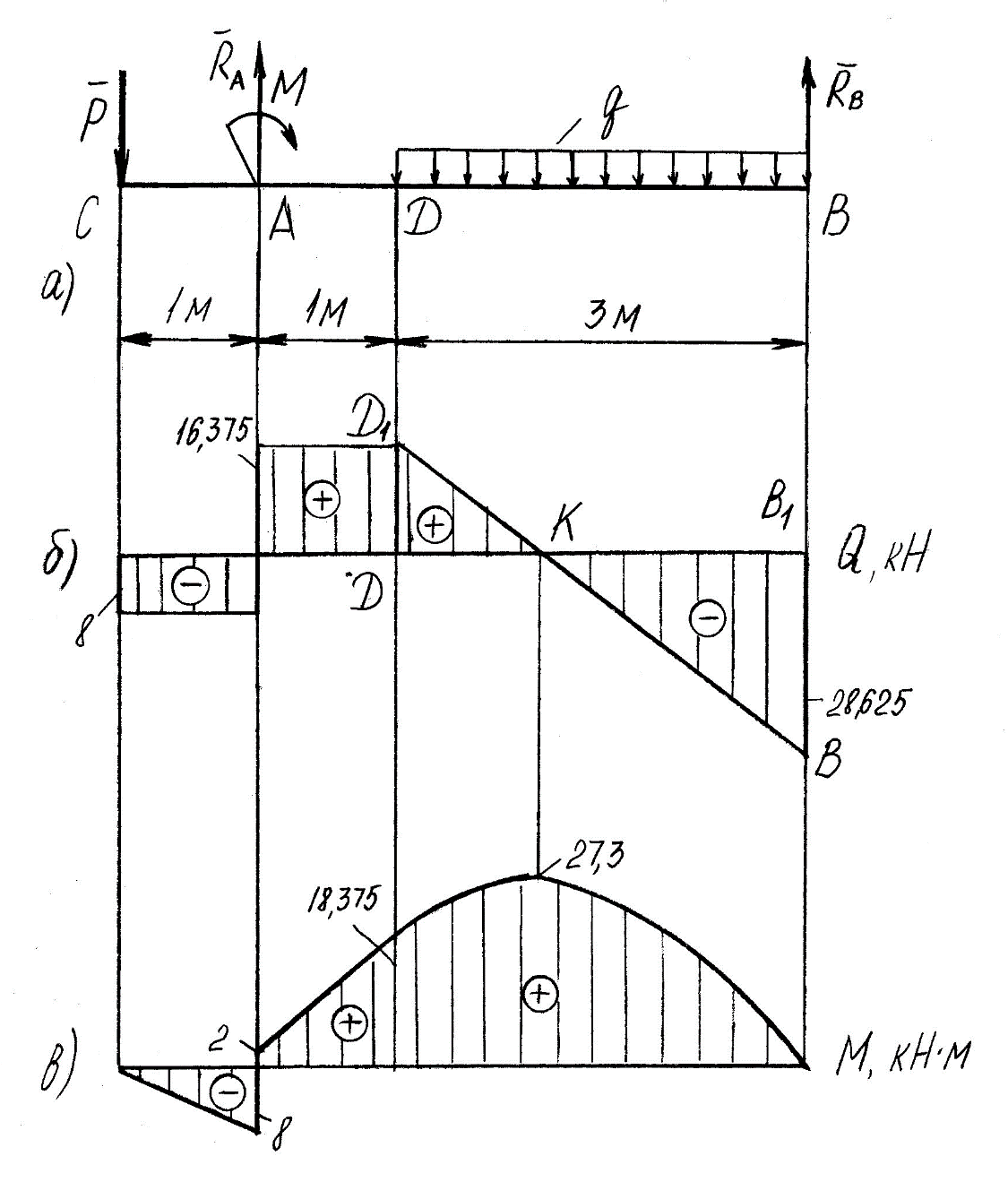 Рисунок 12 Построение эпюр Используя условие прочности при изгибе, подберём поперечное сечение для стальной балки в виде двух швеллеров. Опасное сечение ‒ сечение балки, где действует максимальный момент 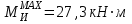 Подбираем размеры балки в опасном сечении по условию прочности 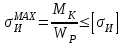 Найдем момент сопротивления 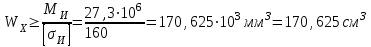 По таблицам сортамента ГОСТ 8240-89 выбираем швеллер №16. Осевой момент сопротивления 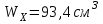 Для двух швеллеров 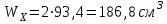 Используя условие прочности при изгибе, подберём поперечное сечение для деревянной круглой балки 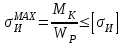 Найдем момент сопротивления 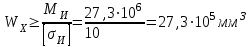 Найдём диаметр круглого сечения 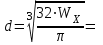 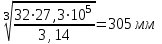 Задание 7 Для стального вала круглого поперечного сечения с одним зубчатым колесом (рисунок 13) определить диаметр вала в опасном сечении.      Допускаемое напряжение   Рисунок 13 Заданная схема вала Решение: Строим расчётно-графическую схему нагружения вала (рисунок 14, а). Проводим оси координат. Ось Х параллельна окружной силе  , ось Y параллельна радиальной силе , ось Y параллельна радиальной силе 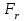 . .Определим момент, передаваемый валом, и крутящий момент 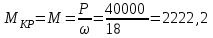 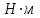 Строим эпюру крутящих моментов (рисунок 14, б). Определим окружную силу 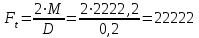 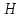 Определим радиальную силу 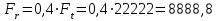 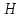 Строим расчётно-графическую схему нагружения вала от окружной силы (рисунок 14, в) и определяем реакцию подшипников от окружной силы 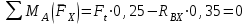 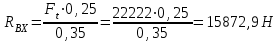 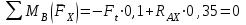 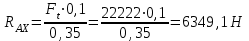 Проверим правильность определения реакций опор, составив уравнение проекций всех сил на ось 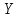 . .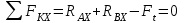 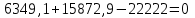 Равенство выполняется, следовательно, опоры определены верно. Строим эпюру изгибающих моментов в вертикальной плоскости (рисунок 14, г) 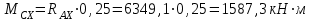 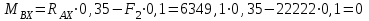 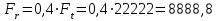 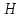 Строим расчётно-графическую схему нагружения вала от радиальной силы (рисунок 14, д) и определяем реакцию подшипников от радиальной силы 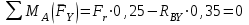 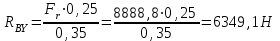 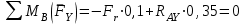 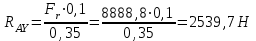 Проверим правильность определения реакций опор, составив уравнение проекций всех сил на ось 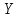 . .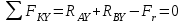 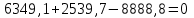 Равенство выполняется, следовательно, опоры определены верно. Строим эпюру изгибающих моментов в вертикальной плоскости (рисунок 14, e) 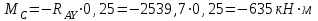 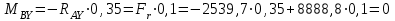 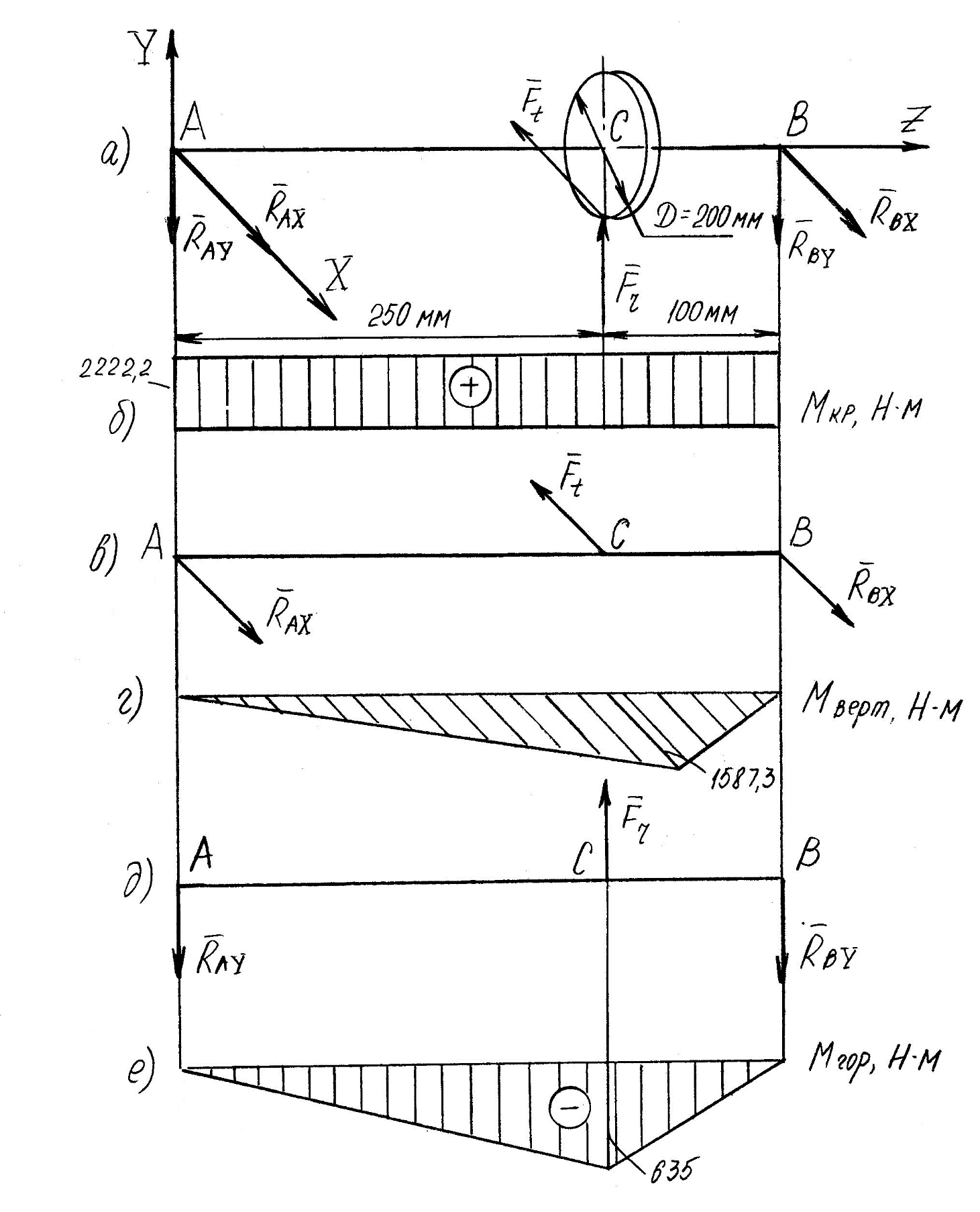 Рисунок 14 Построение эпюр Вычисляем эквивалентный момент в сечении С По гипотезе наибольших напряжений 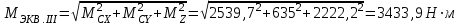 По гипотезе потенциальной энергии формообразования 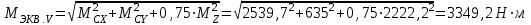 Определим требуемые размеры вала 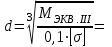 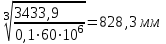 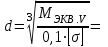 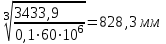 Окончательно принимаем 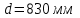 Задание 8 Определить параметры привода: угловые скорости, вращающие моменты, мощности на валах, передаточные отношения, КПД. Описать назначение, принцип работы, устройство привода. Мощность электродвигателя 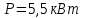 Частота вращения электродвигателя 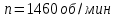 Числа зубьев конических колёс 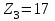 , , 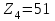 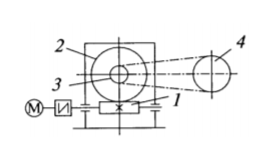 Рисунок 15 Схема привода Решение: Привод двухступенчатый. Первая ступень – закрытая червячная передача. Вторая ступень – цепная передача. Определим общий КПД привода 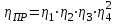 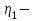 кпд червячной передачи кпд червячной передачи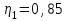 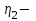 кпд цепной передачи кпд цепной передачи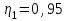 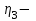 коэффициент, учитывающий потери в муфте коэффициент, учитывающий потери в муфте 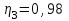 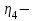 коэффициент, учитывающий потери пары подшипников качения коэффициент, учитывающий потери пары подшипников качения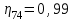 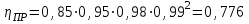 Требуемая мощность двигателя Общее передаточное отношение привода равно произведению частных передаточных чисел ступеней передачи. 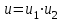 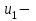 передаточное отношение закрытой цилиндрической передачи передаточное отношение закрытой цилиндрической передачи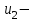 передаточное отношение открытой конической передачи передаточное отношение открытой конической передачиПроизводим разбивку передаточного отношения по ступеням. Передаточное отношение цепной передачи 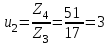 Передаточное отношение червячного редуктора 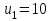 Передаточное число привода 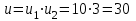 Вычисляем частоту вращения валов: 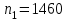 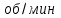   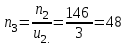 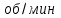 Угловые скорости на валах 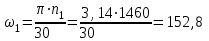 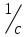 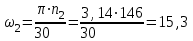 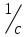 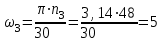 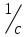 Мощности на валах 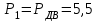 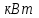   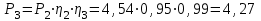 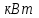 Вычисляем вращающие моменты на валах 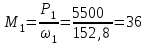 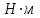 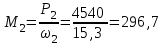 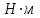   Литература: 1. Андреев В. И., Паушкин А. Г., Леонтьев А. Н. Техническая механика. – М.: Издательство АСВ, 2013 2. Аркуша А. И. Техническая механика. – М.: КД Либроком, 2015 3. Вереина Л. И. Техническая механика. – М.: Академия, 2015 4. Михайлов А. М. Техническая механика. – М.: Инфра-М, 2018 5. Олофинская В. П. Техническая механика. – М.: Инфра-М, 2018 6. Петровский В. В. Техническая механика. – М.: Издательство МГИУ, 2008 7. Эрдеди А. И. Техническая механика. – М.: Академия, 2012 |
