Растяжение и сжатие

• Название: Растяжение и сжатие
• Дата: 19.01.2022
• Размер: 0.66 Mb.
• Имя файла: No_3.docx
• Тип: Закон; #335611

Растяжение и сжатие

Цель работы: Сформировать у студентов навыки использования метода сечения для определения величины внутреннего силового фактора и напряжения.

Задачи: Формирование умения строить эпюры продольных сил и нормальных напряжений, определения с помощью закона Гука величины продольной деформации при растяжении и сжатии.

Задание: Построить эпюры продольных сил и нормальных напряжений по длине бруса, нагруженного, как показано на рис. 14. Определить удлинение (укорочение) бруса, приняв E=2×10⁵МПа.

Данные для своего варианта выбрать из таблицы 3.


Таблица 3

Вариант	F1 [кН]	F2 [кН]	А1 [см2]	А2 [см2]	А3 [см2]	а1 [см]	а2 [см]	а3 [см]	а4 [см]	Схема рис.14
1	95	75	18	18	8	90	30	50	40	1
2	110	90	15	15	8	50	30	40	90	2
3	50	170	18	18	15	10	30	40	50	3
4	10	70	5	5	12	70	80	10	40	4
5	70	120	16	16	12	60	10	40	100	5
6	70	110	16	16	12	80	60	40	50	6
7	150	110	10	10	15	90	20	40	80	7
8	70	120	25	25	12	80	100	50	50	8
9	90	210	16	16	10	10	60	80	70	9
10	60	170	12	12	14	100	30	50	30	10
11	120	70	16	16	8	60	40	80	70	1
12	210	50	18	18	15	50	40	60	80	2
13	50	210	25	25	20	15	30	40	70	3
14	35	75	14	14	20	90	80	20	50	4
15	50	170	30	30	25	50	10	30	90	5
16	70	150	25	25	20	80	70	30	50	6
17	110	90	15	15	18	90	30	50	70	7
18	90	110	35	35	15	40	50	30	30	8
19	70	170	30	30	12	20	80	50	60	9
20	80	150	10	10	12	100	40	30	50	10
21	110	90	20	20	10	40	30	70	50	1
22	120	70	16	16	10	100	50	30	70	2
23	70	120	16	16	12	10	40	70	80	3
24	20	80	10	15	18	50	70	15	60	4
25	90	190	25	15	18	70	15	40	90	5
Вариант	F1 [кН]	F2 [кН]	А1 [см2]	А2 [см2]	А3 [см2]	а1 [см]	а2 [см]	а3 [см]	а4 [см]	Схема рис.14
26	90	110	25	15	18	90	70	30	60	6
27	180	50	12	35	25	90	30	40	90	7
28	50	190	30	20	16	30	50	40	40	8
29	80	150	20	18	10	15	70	90	70	9
30	90	140	14	18	16	70	20	60	20	10

Продолжение таблицы 3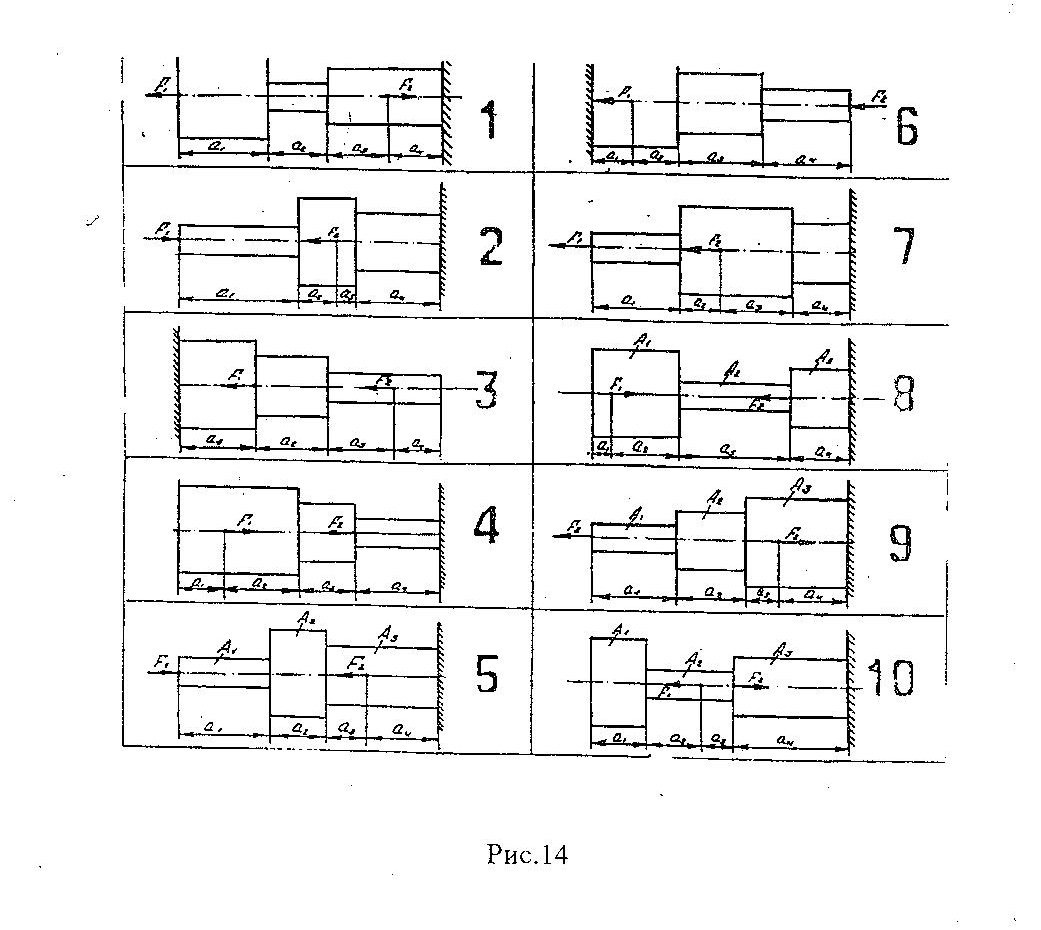




Теоретическое обоснование

Растяжением (сжатием) называется такое нагружение бруса, при котором в поперечном сечений бруса. Численно равная алгебраической сумме проекции внешних сил, действующих на отсеченную часть бруса – на ось Z.

Если N_z положительная, то в этом сечении брус растягивается, а если N_z отрицательная – сжимается.

Эпюра N_z– график показывающий как изменяется величина N_z по длине бруса («скачки» в эпюре N_zнаходятся в местах приложения внешних сил).

Нормальные напряжения определяются по формуле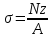



где N_z – продольная сила, возникающая в рассматриваемом сечения;

A – площадь этого поперечного сечения.

Эпюра σ – график, показывающий, как изменяется величина σ по длине бруса («скачки» в эпюре σ находится в местах приложения внешних сил и изменения пощади поперечного сечения бруса).

Удлинение (укорочение бруса определяется по формуле Гука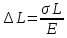



где L– длина участка бруса, в пределах которого действует постоянное по величине напряжение

E– модуль продольной упругости материала бруса.

Последовательность выполнения расчета

1. 
   Намечаем сечения бруса, начиная со свободного от связи конца после точки приложения каждой внешней силы и после мест изменения площади поперечного сечения.
   
2. 
   Для каждого намеченного сечения, отбрасывая связанную часть бруса и уравновешивая отсеченную часть продольной силой, составляем уравнение равновесия ∑Z_i= 0. Из решения того уравнения определяем величину продольной силы N_z/
   
3. 
   По формуле 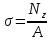определяем нормальные напряжения действующие в каждом поперечном сечении.
   
4. 
   Строим эпюры N_z и σ.
   
5. 
   Определяем удлинение или укорочение бруса по формуле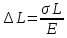
   

.

Пример расчета

Дано: F₁=120 кН; F₂=190 кН; А₁=16 см²; А₂=20 см²; А₃=10 см²; а₁=100 см;

а₂=50 см; а₃=30 см; а₄=70 см; E= 2×10⁵ МПа.

Решение:

1. Намечаем сечения бруса, начиная со свободного от связи конца, т. е. слова на право, после силы F₁ – 1 сечение, после имения площади поперечного сечения бруса – 2 сечение, после силы F₂ – 3 сечение и после следующего изменения площади поперечного сечения бруса – 4 сечение (рис.15).

2. Для каждого намеченного сечения, отбрасывая связанную часть бруса и уравновешивая отсеченную часть продольной силой, составляем уравнения равновесия, из решения которых определяем величины продольных сил:

1) ∑Z_i= - F₁ + N_z^I=0; N_z^I=F₁=120 кН;

2) N_z^II=N_z^I=12 кН

3) ∑Z_i= - F₁ – F₂ + N_z^III=0; N_z^III=F₁+F₂=120+190=310 кН

4) N_z^IV=N_z^III=310 кН

3.Определяем нормальные напряжения, действующие в каждом намеченном сечении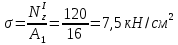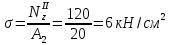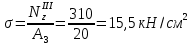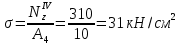

1. 
   
   

2. 
   
   

3. 
   
   

4. 
   
   

4. Строим эпюры N_z и σ, не забывая, что в эпюре продольных сил N_z «скачки» находятся в местах приложения внешних сил, а в эпюре нормальных напряжений σ – в местах приложения внешних сил и в местах изменения площадей поперечных сечений бруса (рис. 15).

5. Определяем изменение длины бруса

∆L = 1/E (σ^Ia₁+σ^IIa₂+σ^IIIa₃+σ^IVa₄) =

=1/2×10⁵(75×1000+60×500+155×300+310×700)=1,8425 мм.

Ответ: ∆L = 1,8425мм

Контрольные вопросы

1. 
   Как нагрузить прямой стержень, чтобы он испытывал только растяжение?
   
2. 
   Что называется эпюрой продольных сил бруса?
   
3. 
   Как строится эпюра продольных сил?
   
4. 
   Как определить нормальное напряжение в поперечном сечении бруса?
   
5. 
   Что называется эпюрой нормальных напряжений?
   
6. 
   Что такое модуль продольной упругости и какова его размерность?
   
7. 
   Какая величина в формуле закона Гука характеризует жесткость материала?
   
8. 
   Зависит ли нормальное напряжение от материала бруса и формы поперечного сечения?
   
9. 
   Зависит ли удлинение бруса от его материала?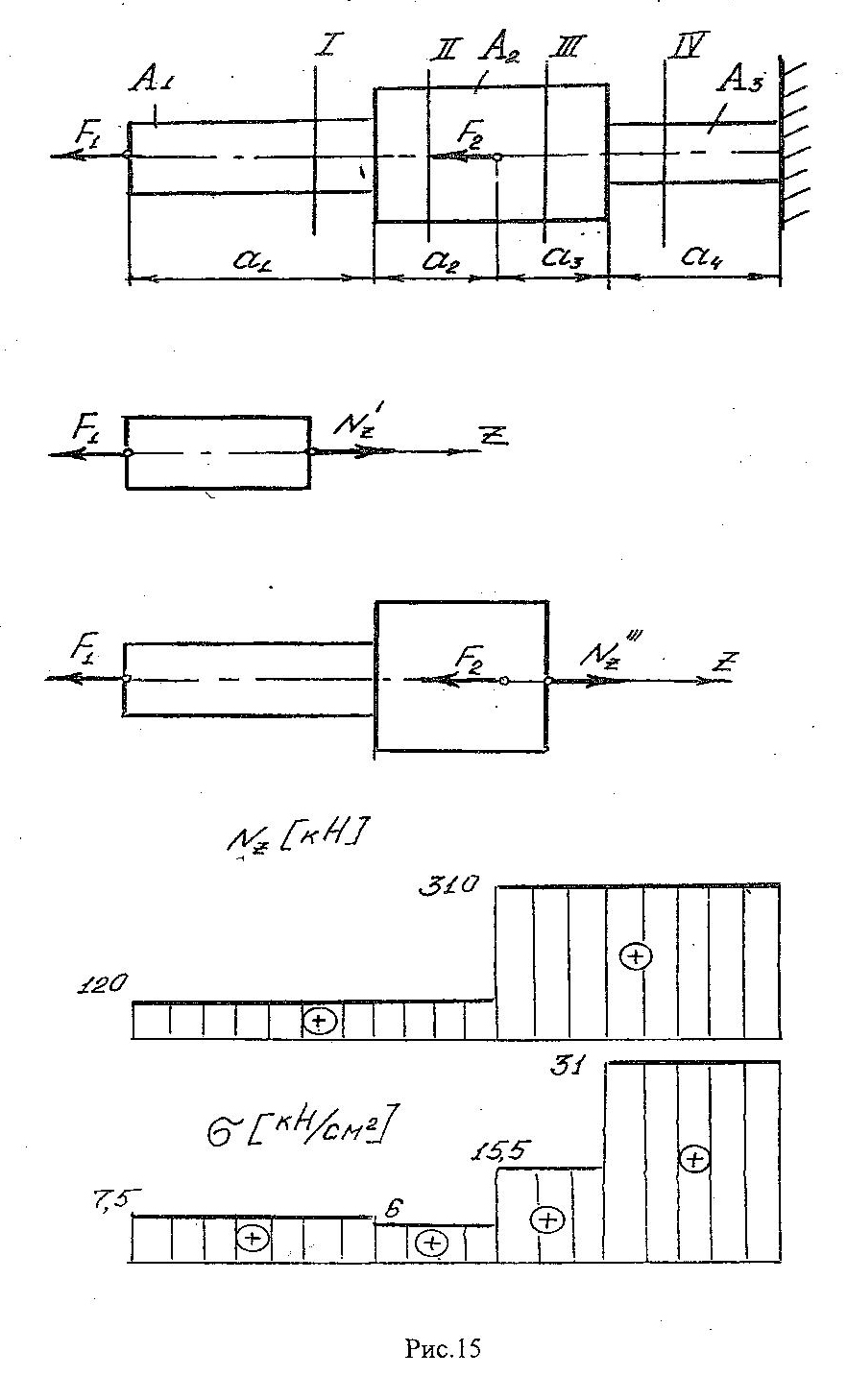