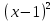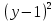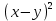Уравнения в целых числах. Разложение на множители
 Скачать 36.55 Kb. Скачать 36.55 Kb.
|
|
Уравнения в целых числах Разложение на множители Пример: Решить в целых числах (x-1)(y+3)=19. Так как 19 – простое число, то оно может быть представлено как произведение двух целых чисел в четырёх различных вариантах: 19=19·1; 19=1·19; 19=(-19)·(-1); 19=(-1)·(-19), таким образом, (x-1)(y+3) =19  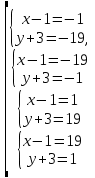 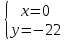 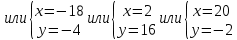 . . (20;-2), (2;16), (-18;-4), (0;-22). (20;-2), (2;16), (-18;-4), (0;-22).Упражнения (x-1)(y+15)=3 Ответ:(4;-14),(2;-12),(0;-18),(-2;-16) (2х+3)(у-1)=7 Ответ:(2;2),(-1;8),(-5;0),(-2;-6) (1-х)(22+у)=971 Ответ:(972;-21),(0;949),(2;-993), (972;-23) х(23у-98)=0 Ответ:(0;z) , z 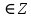 (х+2000)(у-2000)=2 Ответ:(-1998;2001),(-1999;2002), (-2001;1998), (-2002;1999) Прежде чем решать некоторые примеры подобным способом, их надо разложить на множители. Например, х + у = ху. Первым действием перенесём все слагаемые в одну часть: ху-х-у=0,далее, чтобы разложить пример на множители обычно к каждой из частей добавляют удобное целое число. В нашем примере постараемся получить произведение (х-1)(у-1), добавив к каждой из частей уравнения 1,то есть ху-х-у+1=1. Разложив на множители, получим (х-1)(у-1)=1,откуда х=0,у=0 или х=2, у=2. Немного более сложной является задача 3х2+4ху-7у2=13. Разложением на множители получим (х-у)(3х-7у)=13, заметим, что в данном случае ничего не прибавляем к обеим частям уравнения. Так как 13=13·1=1·13=-13·(-1)=-1·(-13), то получим совокупность четырёх систем 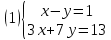 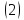 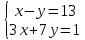  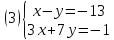 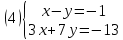 Решая системы, получаем, что системы (2) и (3) решений в целых числах не имеют, а ответами систем (1) и (4) являются соответственнох=2,у=1 и х=-2, у=-1. Решая подобные задачи важно знать, сколько делителей имеет число. Теорема: если произвольное число a=pmqn , гдеpи q– простые числа, а m,n 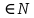 , то число натуральных делителей этого числа а равняется (m+1)(n+1). , то число натуральных делителей этого числа а равняется (m+1)(n+1).Доказательство: запишем по горизонтали все натуральные делители числа pm, по вертикали – все делители натурального числа qn: n+1 раз 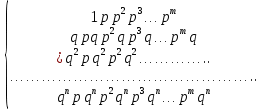 Получили прямоугольник, найдем недостающие делители. Таким образом, общее число натуральных делителей есть площадь прямоугольника со сторонами (n+1) и (m+1), то есть (m+1)(n+1). Иногда предлагается решать уравнения только в простых числах. Пример. Решить уравнение 19х-уz=1995, причём x, y, z - простые числа. Решение: так как 1995 делится нацело на 19, то разложим данное уравнение на множители следующим образом: 19х-уz=1995  уz =19х-1995 уz =19х-1995  уz=19(х-105). Далее, решая в простых числах, получим совокупность двух систем, уz=19(х-105). Далее, решая в простых числах, получим совокупность двух систем, 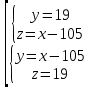  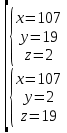 Ответ:(107;19;2), (107;2;19). Делимость чисел Отдельную группу уравнений, решаемых в целых числах, представляют собой уравнения, решения которых в той или иной степени связаны с делимостью. Повторим некоторые признаки делимости, которые нам известны: На 2 делится нацело число, если его последняя цифра чётная. На 4 делится нацело число, если его последние две цифры образуют число, делящееся на 4. На 3 делятся нацело те числа, у которых сумма цифр делится на 3; на 9- те у которых сумма цифр делится на 9. На 5 делятся нацело те числа, у которых последняя цифра 0 или 5. На 6 делятся нацело те числа, которые одновременно делятся на 2 и 3. На 8 делится нацело число, если три последние его цифры образуют число, делящееся на 8. Пример. Решим уравнение: у2 = 5х2 +6. Решение. Предположим, что х 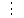 3, тогда 5х2 +6 3, тогда 5х2 +6 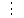 3, но 5х2 +6 не является полным квадратом, так как 5х2 +6 не делится нацело на 9; таким образом, если х 3, но 5х2 +6 не является полным квадратом, так как 5х2 +6 не делится нацело на 9; таким образом, если х 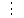 3, то решений нет. Предположим, что х не делится нацело на 33, тогда х2 при делении на 3 даёт в остатке один, в то время как 5х2 +6 при делении на 3 дает в остатке 2, таким образом, остаток правой части не равен остатку левой от деления на одно и то же число, то есть правая часть не равна левой, решений нет. 3, то решений нет. Предположим, что х не делится нацело на 33, тогда х2 при делении на 3 даёт в остатке один, в то время как 5х2 +6 при делении на 3 дает в остатке 2, таким образом, остаток правой части не равен остатку левой от деления на одно и то же число, то есть правая часть не равна левой, решений нет.Ответ: 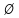 . .Выражение одной переменной через другую Многие целочисленные уравнения решают, выражая одну переменную через другую. Решим уравнение: 2х2 – 2ху +9х +у =2. Решение. Выразим у через х, получим, что у = 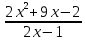 . Далее попробуем сделать так, чтобы в числителе осталось целое число: у = . Далее попробуем сделать так, чтобы в числителе осталось целое число: у = 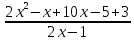  у = х +5 + 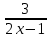 . Так как у . Так как у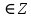 , то , то 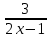 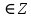 , таким образом, , таким образом, 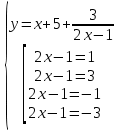  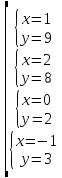 Ответ: (1;9), (2;8), (0;2), (-1;3). Решите самостоятельно уравнение: x2 + 5y2 = 20z +2. ( Ответ: решений нет) ( решение. x2 + 5y2 = 20z +2  5y2 = 20z+2-x2 5y2 = 20z+2-x2  y2 = 4z + y2 = 4z + 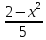 , то есть y2 , то есть y2 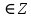 если 4z если 4z 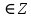 , что верно, и если 2- х2 , что верно, и если 2- х2 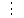 5, что не верно, так как х2 не может заканчиваться на 2, и на 7. Решений нет) 5, что не верно, так как х2 не может заканчиваться на 2, и на 7. Решений нет)Решим уравнение: x2 + 9y2 =3z +2  9y2 = 3z + 2 – x2 9y2 = 3z + 2 – x2  y2 = y2 = 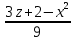 . Пусть . Пусть 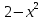 не делится нацело на 3, тогда не делится нацело на 3, тогда 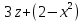 не кратно трём и, следовательно, не кратно 9. Тогда не кратно трём и, следовательно, не кратно 9. Тогда 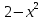 кратно 3, что не возможно, так как при делениина3 квадрат дает в остатке0 или 1, а кратно 3, что не возможно, так как при делениина3 квадрат дает в остатке0 или 1, а 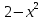 дает в остатке 2 или 1. Число 0 не является составляющей цикла, таким образом дает в остатке 2 или 1. Число 0 не является составляющей цикла, таким образом 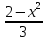 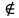 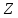 . Решений нет. . Решений нет.Использование чётности – нечетности Решим уравнение 2х- 15 = у2 в натуральных числах. Рассмотрим два случая: x=2k+1; k 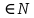 (нечетное число). Так как 2 в четной степени при делении на 3 дает остаток 1, то 22k+1 при делении на 3 дает в остатке 2, 15 делится на 3. Следовательно, y2 не делится на 3, но квадрат числа, не делящегося на 3,дает при делении на 3 в остатке 1. Таким образом равенство невозможно. (нечетное число). Так как 2 в четной степени при делении на 3 дает остаток 1, то 22k+1 при делении на 3 дает в остатке 2, 15 делится на 3. Следовательно, y2 не делится на 3, но квадрат числа, не делящегося на 3,дает при делении на 3 в остатке 1. Таким образом равенство невозможно.x=2k; k 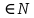 ( четное число), тогда 22k -15 = y2 ( четное число), тогда 22k -15 = y2  22k - y2 =15 22k - y2 =15  (2k –y)( 2k +y) = 15 (2k –y)( 2k +y) = 15  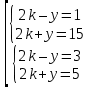 ( в других случаях будут нецелые или ненатуральные решения) ( в других случаях будут нецелые или ненатуральные решения)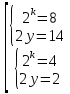  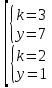 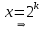 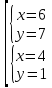 . .Ответ: (6;7), (4;1). В некоторых случаях, решая подобные уравнения, можно найти очевидные корни и доказать, что других нет. Например, в уравнении y2+1=2x любой решающий без особого труда укажет очевидные решения: (0;0), (1;1), (1;-1). Далее рассматривается два случая: x -нечетный, тогда 2x 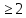 и y2+1 не делится на 2 если y - четный; y2+1 и y2+1 не делится на 2 если y - четный; y2+1 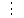 2, если y- нечетный. Однако, если y - нечетный, то y2+1 не делится на 4 т.к. 4k2+4k+2 не делится на 4. 2, если y- нечетный. Однако, если y - нечетный, то y2+1 не делится на 4 т.к. 4k2+4k+2 не делится на 4.А 2х 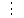 4 при 4 при 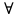 x x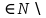 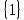 ,таким образом, решений нет. ,таким образом, решений нет.Ответ: (0;0), (1;1), (1;-1). Четность переменных должна также учитываться при решении уравнений вида 2x2 – 5y2 = 7: 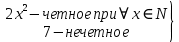 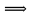 5y2 – нечетное. Таким образом, y – нечетный (y = 2k + 1 : k 5y2 – нечетное. Таким образом, y – нечетный (y = 2k + 1 : k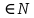 ), подставив y = 2k + 1, получим уравнение 2x2 -5(2k + 1)2 = 7 ), подставив y = 2k + 1, получим уравнение 2x2 -5(2k + 1)2 = 7  x2- 10k2 – 10k = 6. Следовательно, х должен быть четным (х= 2n : n x2- 10k2 – 10k = 6. Следовательно, х должен быть четным (х= 2n : n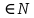 ), подставив x = 2n, получим уравнение 4n2-10k2-10k=6 ), подставив x = 2n, получим уравнение 4n2-10k2-10k=6  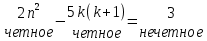 , таким образом, данное уравнение не имеет решений, то есть и исходное уравнение их тоже не имеет. , таким образом, данное уравнение не имеет решений, то есть и исходное уравнение их тоже не имеет.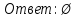 . .Задача. Найти три целых решения и общий вид решений уравнения x2 – 51y2 = 1. Выразим у2 через х2: у2 = 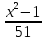 , можно найти очевидные решения: , можно найти очевидные решения: 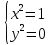 и общий вид решений данного уравнения: и общий вид решений данного уравнения: 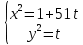 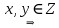 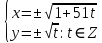 , то есть помимо решений (1;0), (-1;0), принимая t за полные квадраты (1;4;9;165;25;36;…), можно найти решение (50;7). , то есть помимо решений (1;0), (-1;0), принимая t за полные квадраты (1;4;9;165;25;36;…), можно найти решение (50;7).Ответ: (1;0), (-1;0), (50;7), ( 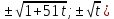 : : 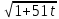 , , 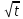 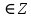 . .Метод преобразования уравнения в сумму квадратов. Оценки Решим уравнение: 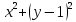 = 1 в целых числах. Очевидно, что если сумма двух квадратов равна 1, то либо один из них равен нулю, другой – 1, либо наоборот. Таким образом, = 1 в целых числах. Очевидно, что если сумма двух квадратов равна 1, то либо один из них равен нулю, другой – 1, либо наоборот. Таким образом, 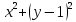 = 1 = 1 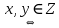 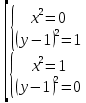  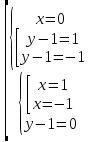  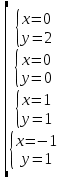 . .Ответ: (0;2), (0;0), (1;1),(-1;1). Собственно само преобразование в сумму квадратов выглядит следующим образом: x + y = x2 – xy + y2  x2 – x – xy – y + y2 = 0 x2 – x – xy – y + y2 = 0  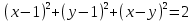  … …  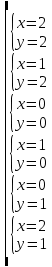
Ответ: (2;2),(1;2), (0;0), (1;0), (0;1),(2,). Уравнения вида 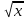 + + 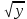 = = 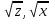 + + 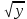 = z, где z = z, где z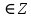 . .Решим уравнение: 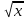 + + 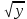 = = 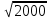 . .Вынесем 202 = 400 из-под радикала: 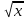 + + 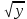 =20 =20 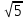  x = x = 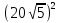 -40 -40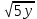 + y + y  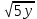 = = 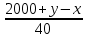 , причем , причем 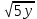 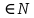 и и 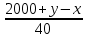 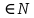 . .Таким образом, y=5k2 : k 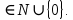 Поскольку Поскольку 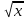 + + 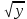 =20 =20 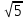 , то x= 5m2 : m , то x= 5m2 : m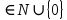 , причем k + m = 20, что равносильно совокупности , причем k + m = 20, что равносильно совокупности 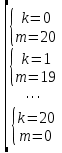 , то есть , то есть 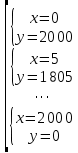 . .Ответ: (5 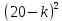 ; 5k2) , где k= 0;1;2; …, 20. ; 5k2) , где k= 0;1;2; …, 20.Уравнение 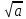 + + 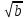 = 48, вида = 48, вида 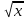 + + 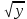 = z, где z = z, где z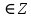 , решается в целых числах следующим образом: , решается в целых числах следующим образом: 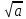 + + 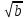 = 48 = 48  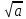 + + 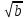 = 12 = 12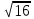 , таким образом, a= 16k2(смотри предыдущую задачу), аналогично b=16m2, причем k + m = 12 и k,m , таким образом, a= 16k2(смотри предыдущую задачу), аналогично b=16m2, причем k + m = 12 и k,m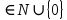 , таким образом, , таким образом, k + m = 12; k 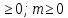  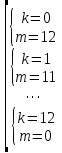 , то есть , то есть 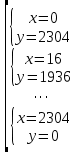 . .Ответ: (0;2304), (16;1936), …, (2304;0). Решите самостоятельно: 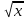 + + 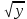 = = 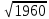 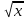 + + 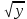 = = 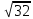 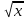 + + 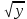 = 1960 = 1960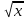 + + 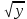 = = 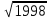 . . |