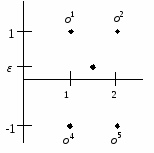Анализ данных. Разложение суммы квадратов в однофакторном да

• Название: Разложение суммы квадратов в однофакторном да
• Анкор: Анализ данных.doc
• Дата: 16.02.2018
• Размер: 2.64 Mb.
• Имя файла: Анализ данных.doc
• Тип: Документы; #15612
• Категория: Информатика. Вычислительная техника
• страница: 5 из 6

Оценка общностей. Проблемы оценки общностей и оценки факторов тесно переплетаются. Если значения общностей установлены, то матрица становится полностью известной и для нее может быть установлен ранг, т.е. минимально необходимое число общих факторов. Если вначале установлено число m общих факторов, то значения общностей подбирают таким образом, чтобы ранг матрицы приближался к этому числу. Существует несколько способов оценивания общности. Мы их рассмотрим вкратце, поскольку при большом числе переменных точность оценивания общностей практически не сказывается на результатах факторного анализа.

Наиболее теоретически обоснован и чаще всего рекомендуется в качестве оценки общности i-го признака коэффициент множественной корреляции i-го исходного признака с остальными (n–1) признаками.

Значение вычисляется по формуле: , (11.11)

где – диагональный элемент обратной корреляционной матрицы .

При проведении факторного анализа на ЭВМ во многих случаях используют итерационную процедуру вычисления общностей. На каждой итерации с помощью метода главных факторов определяют матрицу факторных нагрузок, а по ней находят оценки общностей, которые используются в следующей итерации. В качестве начaльного приближения используют коэффициент множественной корреляции (11.11).

Вращение факторов. Исследование с помощью факторного анализа следует признать успешным, если выявлено не только число общих факторов, но и дано содержательное толкование тем внутренним, скрытым причинам (общим факторам), которые обусловили результаты наблюдений. С целью облегчения процесса интерпретации общих факторов осуществляется третий этап факторного анализа – вращение факторов. Выше указывалось, что матричное уравнение имеет бесконечное число решений (с точностью до ортогонального преобразования Т). Рассмотренные методы выделения факторов однозначно устанавливают положение системы координат, однако за счет введения дополнительных ограничений. Оси, соответствующие общим факторам, ориентируются последовательно по максимуму оставшейся дисперсии. Такая ориентация координат оказывается существенной в методе главных компонент, ориентированном на дисперсии. Основная цель факторного анализа – объяснение корреляций между исходными признаками. Окончательную ориентацию осей координат здесь производят из других соображений, а именно: с точки зрения содержательной интерпретации общих факторов. Для этого систему координат в пространстве общих факторов поворачивают как целое вокруг ее начальной точки, что эквивалентно умножению факторного отображения В на ортогональную матрицу Т справа.

Процедуру вращения рассмотрим на примере. По результатам успеваемости построена корреляционная матрица оценок по шести предметам: математике, физике, истории, литературе, родному языку, иностранному языку. Одним из методов выделены два общих фактора. Корреляционная матрица и матрица факторных нагрузок приведены в табл.26.

Таблица 26

№ признака	Корреляционная матрица						Общий фактор1	Общий фактор2
1	1	0,50	0,32	0,20	0,22	0,12	0,6	0,6
2	0,50	1	0,21	0,15	0,16	0,07	0,4	0,4
3	032	0,21	1	0,44	0,67	0,41	0,7	0,2
4	0,20	0,15	0,44	1	0,56	0	0,6	-0,2
5	0,22	0,16	0,67	0,56	1	0,51	0,8	-0,4
6	0,12	0,07	0,41	0,33	0,51	1	0,5	-0,3

Интерпретация полученных общих факторов представляет определенные трудности: необходимо выявить то общее, что обусловило высокие нагрузки на все шесть предметов у первого фактора, и на первый, второй и пятый – у второго, причем последняя значимая нагрузка − отрицательна.

На рис. 14 приводится графическая иллюстрация полученного факторного отображения (номера точек 1-6 соответствуют строкам матрицы факторного отображения).



Рис.14. Поворот системы координат
Повернем оси координат по часовой стрелке так, чтобы сгусток, состоящий из точек 3-6, оказался как можно ближе к оси . Угол поворота составляет как видно из рисунка, . Матрица преобразования T координат при повороте на угол по часовой стрелке имеет вид: .

Новые координаты точек В_н получаются перемножением матриц В и T , т.е. . (11.12)

Для рассматриваемого примера получим: .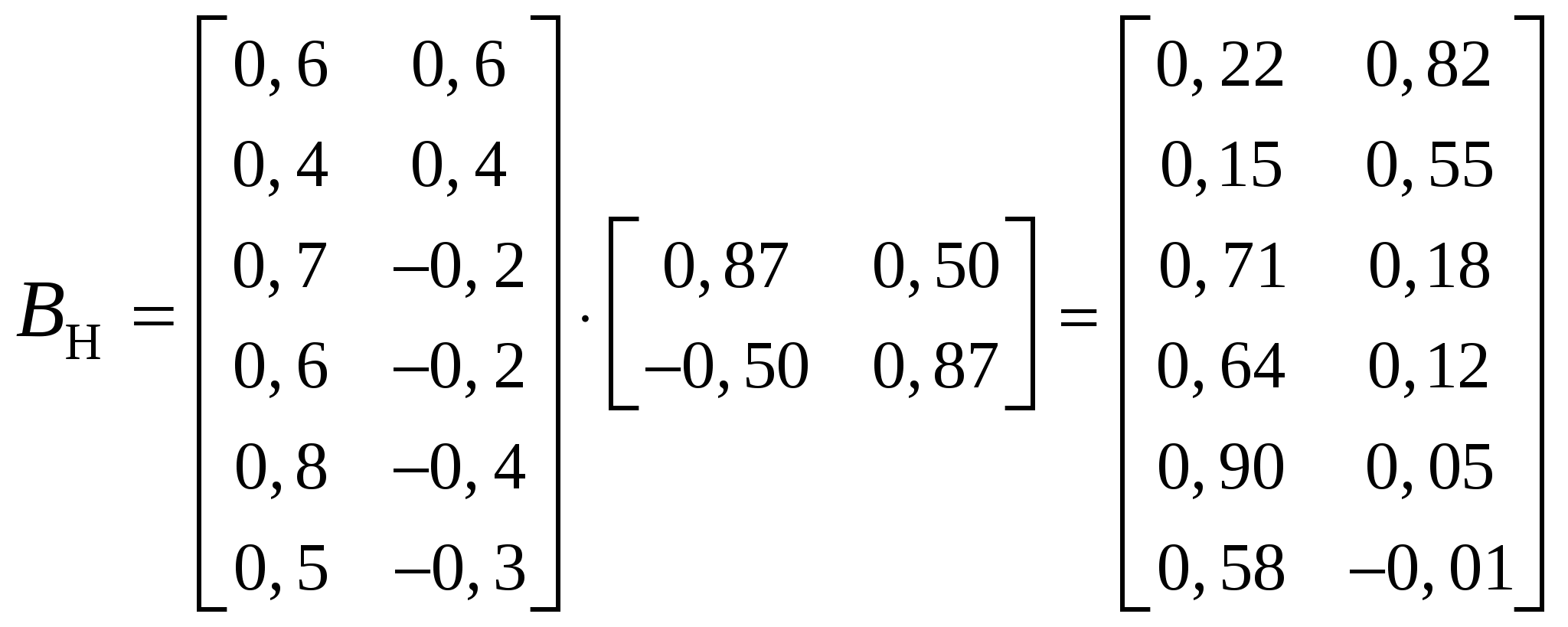

Интерпретация факторов, отвечающих матрице , несомненно проще: первый фактор существенно нагружает теперь только четыре исходных признака (история, литература, родной и иностранный языки), а второй первые два признака (математика, физика), причем значимых отрицательных нагрузок нет. Естественно первый фактор назвать, например, гуманитарной одаренностью, а второй – склонностью к точным наукам.

Рассмотренный пример явился иллюстрацией геометрического подхода к проблеме вращения. Он предполагает визуализацию факторного отображения с последуюшим поворотом системы координат так, чтобы новые оси проходили через скопления точек. Если число общих факторов больше двух, то вращение осуществляется по шагам, учитывая каждый раз одновременно только две оси. Полная матрица преобразования состоит из произведения отдельных матриц преобразования для всех комбинаций пар факторов.

Только что рассмотренный пример на вращение показывает, что интерпретация общих факторов тем проще, чем «контрастнее» будут значения нагрузок – элементы столбца матрицы факторного отображения: либо близки к нулю, либо к единице. В этом случае каждый исходный признак получает наиболее простое описание на языке общих факторов (11.10) и, наоборот, при интерпретации каждого общего фактора учитывается минимальное число исходных признаков. Именно эти соображения легли в основу концепции простой структуры, широко используемой в факторном анализе. Термин «простая структура» служит для характеристики взаимосвязи между конфигурацией векторов, соответствующих исходным признакам, и осями координат пространства общих факторов. Если конфигурация векторов такова, что позволяет вращением координат достигнуть положения, при котором значительное большинство векторов-признаков окажутся на гиперплоскостях координат или вблизи них, то в этом случае говорят о простой структуре.

При многомерном факторном анализе в каждом столбце матрицы факторных нагрузок B найдутся несколько элементов, близких к нулю. Отсюда возникает вопрос: какое количество нулевых нагрузок достаточно, чтобы считать найденную гиперплоскость значимой? Решить этот вопрос можно с помощью критерия Баргмана. Для очередного i-го общего фактора подсчитывают число признаков, для которых выполняется условие . Это число, называемое числом нулевых нагрузок, сравнивают с табличным q_Т, соответствующим определенному числу исходных признаков. Если при выбранном уровне значимости, то этот фактор считается определенным и его можно интерпретировать. Критерий Баргмана проверяет по сути дела гипотезу, что векторы, отвечающие исходным признакам, лежат друг к другу плотнее, чем можно было бы ожидать при случайном их расположении в пространстве общих факторов.

Кроме геометрического подхода к вращению факторов применяется аналитический подход. Применение этого подхода потребовало выработки критерия, с помощью которого можно было бы сравнивать результаты вращения.

Такой критерий опирается на концепцию простой структуры. В качестве меры простоты фактора выбирается дисперсия квадратов его нагрузок. Если эта дисперсия максимальна, то отдельные нагрузки близки к нулю или единице. Взяв сумму дисперсии по всем факторам и приводя векторы-признаки к единичной длине, получаем так называемый варимакс-критерий: .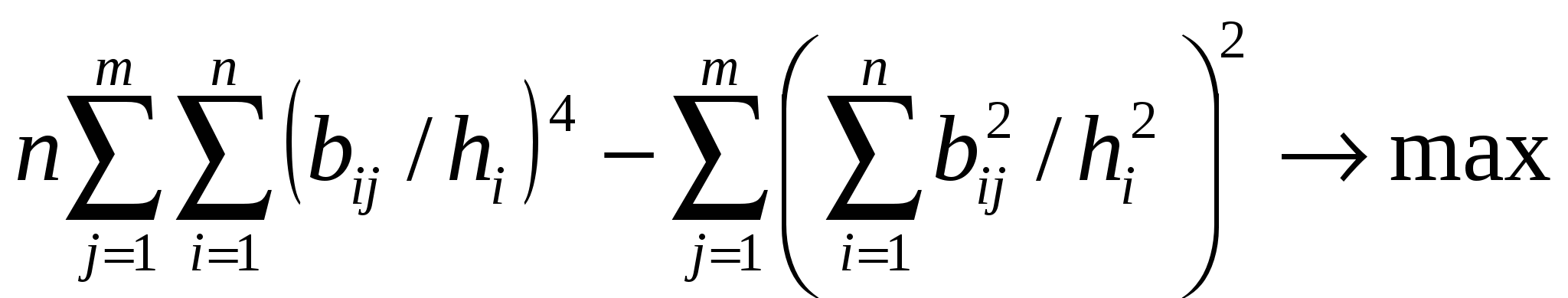

Процедура вращения осуществляется последовательно, учитывая каждый раз только две оси. Производится поворот на некоторый небольшой угол. Факторные нагрузки пересчитываются по формуле (11.12). Если при этом значение варимaкс-критерия возрастает, то эти оси вновь поворачиваются на тот же самый угол. Если же значение варимакс-критерия уменьшится, то переходят к другой паре координатных осей, и процедура повторяется.
18. Меры близости и различия в кластерном анализе.
Функции расстояния и сходства Неотрицательная вещественная функция называется функцией расстояния (метрикой), если:
а) для всех и из ;

б) лишь для ;

в) ;

г) , где − любые три точки из (так называемое “правило треугольника”).

Значение функции d для двух заданных точек эквивалентно расстоянию между Оⁱ и О^j.

В качестве примера функций расстояний приведем наиболее употребительные:

1. 
   евклидово расстояние ;
   

2) сумма абсолютных отклонений, называемая иногда метрикой города, ;

3) расстояние Махаланобиса ,

где – матрица, обратная матрице рассеяния (см. (9.3)) .

Расстояние Махаланобиса часто называют обобщенным евклидовым расстоянием; оно инвариантно относительно невырожденного линейного преобразования Υ=BХ, то есть .

Первые две метрики представляют частный случай так называемой 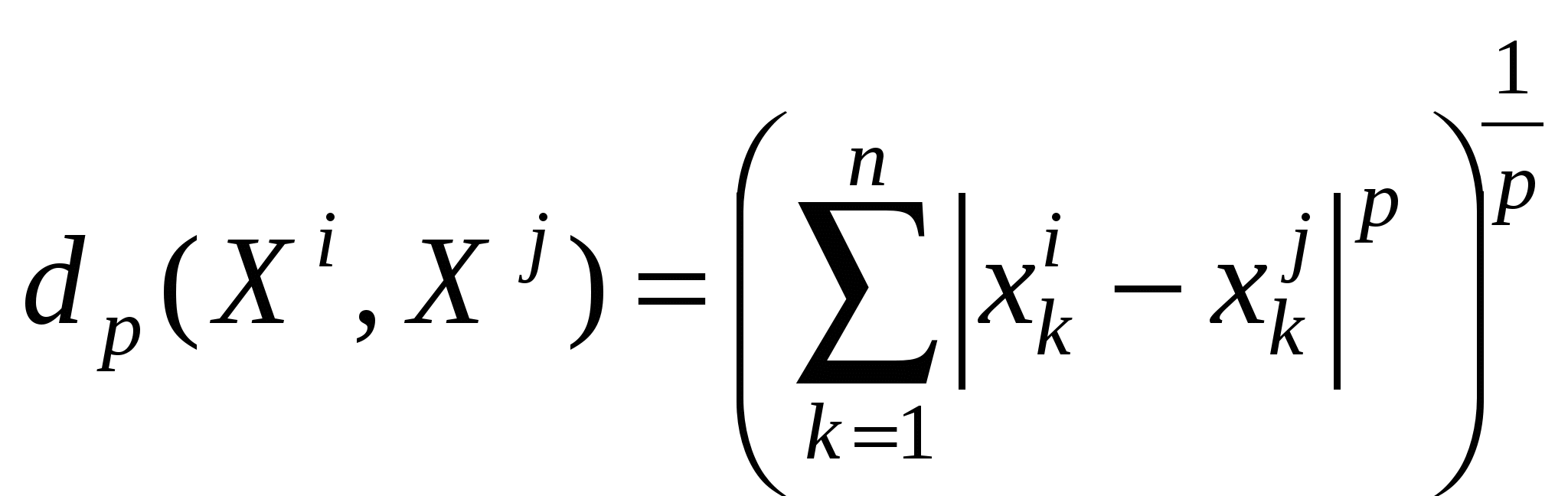-метрики:

.

Для -метрики справедливо соотношение для любых тогда и только тогда, когда .

Обобщением l_p-метрики является «взвешенная» l_p-метрика ,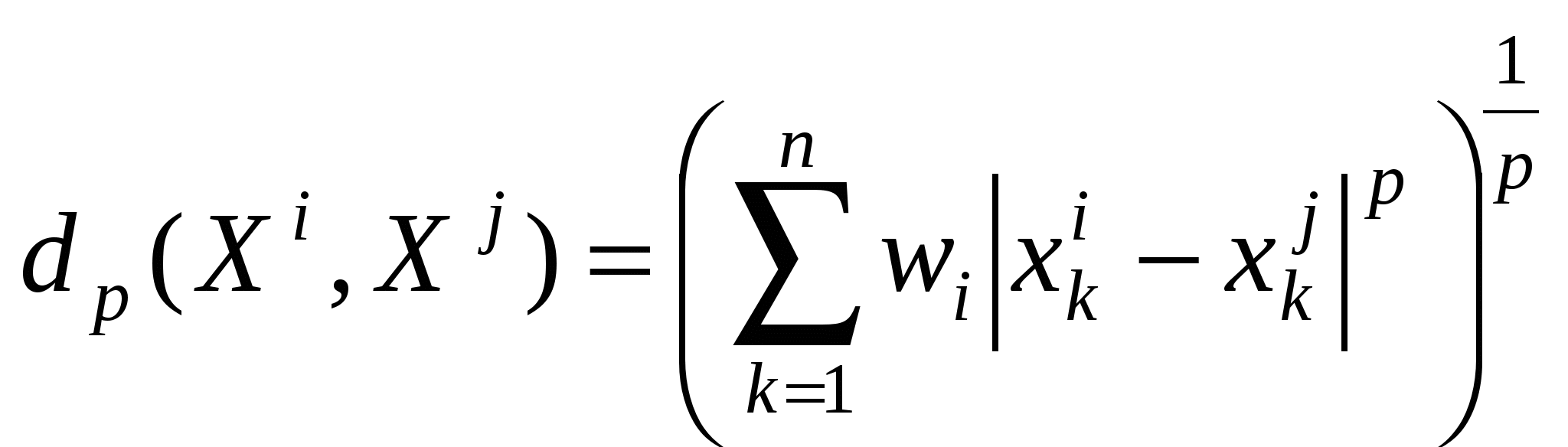

где w_i – некоторый неотрицательный «вес», пропорциональный степени важности i-й компоненты при решении вопроса об отнесении объекта к тому или иному классу.

Расстояния между N объектами могут быть сведены в квадратную симметричную матрицу расстояний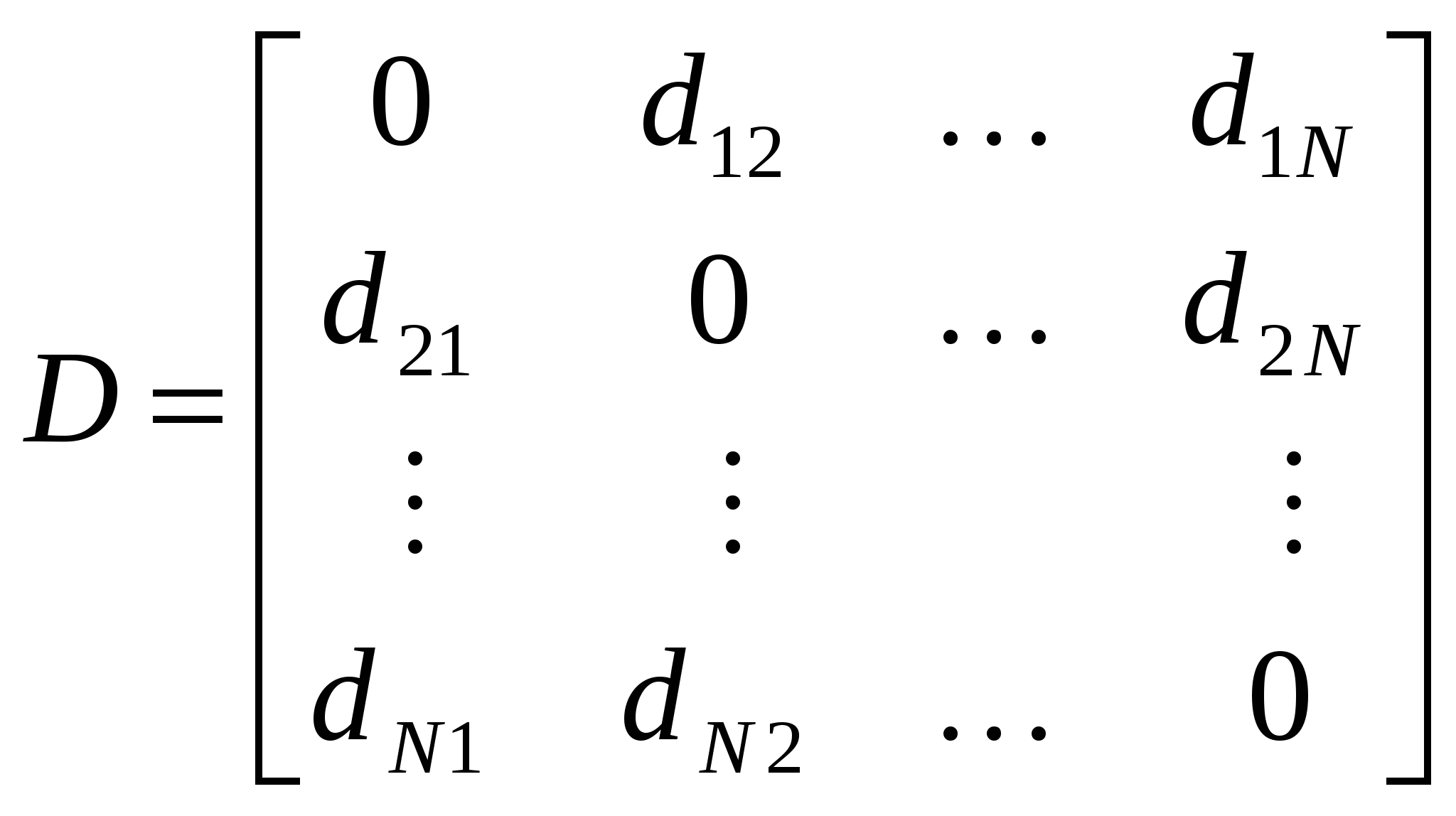

. (9.2)

Понятием, противоположным расстоянию, является понятие сходства. Мерой сходства называют неотрицательную вещественную функцию, удовлетворяющую следующим аксиомам:

1) ;

2) ;

3) .

Значения функции сходства элементов множества О можно объединить в матрицу сходства

.

Величину обычно называют коэффициентом сходства. Приведем в качестве примера функции сходства для объектов, описываемых дихотомическими признаками, т.е. такими, которые могут принимать значения нуль или единица. Для заданных точек и обозначим через число совпадающих единичных (нулевых) координат, через – число координат, имеющих 1 в и 0 в , сходным образом определяется . Мерами сходства будут функции:

1) ; 2) ; 3) .

Заметим, что подбирая подходящее преобразование, можно перейти от мер расстояния к мерам сходства.

Меры близости и расстояния могут задаваться также с помощью так называемых потенциальных функций F(U,V)= f(d(U,V)), где U и V – любые две точки из Е_n, d(U,V) – метрика. В качестве примера приведем две такие функции: F(U,V) = exp(– ad²(U,V)), a>0; F(U,V) = (1 + ad²(U,V))^-1.

Выбор той или иной метрики (или меры близости) является ответственным этапом кластерного анализа, оказывая существенное влияние на результаты разбиения объектов на классы. В каждой конкретной задаче этот выбор должен производиться с учетом целей исследования, физической и статистической природы наблюдений, полноты априорных сведений о характере распределения наблюдений. Приведем несколько рекомендаций по выбору метрики.

1. Если известно, что наблюдения извлекаются из нормальных генеральных совокупностей с одной и той же матрицей ковариаций, то целесообразно использовать расстояние Махаланобиса.

2. Использование обычного евклидова расстояния можно признать оправданным, если:

а) компоненты вектора наблюдений взаимно независимы и имеют одну и ту же дисперсию;

б) отдельные признаки однородны по физическому смыслу и одинаково важны с точки зрения задачи классификации;

в) пространство признаков совпадает с геометрическим пространством (n= 1, 2, 3).

В некоторых задачах связи между объектами вытекают из сущности самой задачи, требуется лишь «подкорректировать» их с тем, чтобы они удовлетворяли аксиомам мер расстояния или сходства. Примером может служить задача классификации с целью агрегирования отраслей народного хозяйства, решаемая на основе матрицы межотраслевого баланса.

Рассмотрим теперь меры близости между кластерами. Введение понятия расстояния между группами объектов оказывается целесообразным при конструировании многих процедур кластеризации. Пусть К_i – i-й кластер, содержащий объектов; – арифметическое среднее наблюдений, входящих в K_i, т.е. – выбранная метрика.

Рассмотрим наиболее употребительные расстояния между кластерами:

1) расстояние, измеряемое по принципу ближайшего соседа (nearestneighbour)

;

2) расстояние, измеряемое по принципу дальнего соседа (furthestneighbour)

;

3) статистическое расстояние между кластерами ;

4) расстояние, измеряемое по центрам тяжести кластеров .

Легко видеть, что пропорционально , если в качестве метрики используется евклидово расстояние;

5) мера близости, основанная на потенциальной функции F(K_l,K_m) =

Иллюстрация трех приведенных мер представлена на рис. 8.



Рис.8. Примеры расстояний между кластерами

19. Метод k-средних в кластерном анализе.

Задача кластерного анализа носит комбинаторный характер. Прямой способ решения такой задачи заключается в полном переборе всех возможных разбиений на кластеры и выбора разбиения, обеспечивающего экстремальное значение функционала. Такой способ решения называют кластеризацией полным перебором. Аналогом кластерной проблемы комбинаторной математики является задача разбиения множества из n объектов на m подмножеств. Число таких разбиений обозначается через S(n,m) и называется числом Стирлинга второго рода. Эти числа подчиняются рекуррентному соотношению: .

При больших n .

Из этих оценок видно, что кластеризация полным перебором возможна в тех случаях, когда число объектов и кластеров невелико.

К решению задачи кластерного анализа могут быть применены методы математического программирования, в частности динамического программирования. Хотя эти методы, как и полный перебор, приводят к оптимальному решению в классе всех разбиений, для задач практической размерности они не используются, поскольку требуют значительных вычислительных ресурсов. Ниже рассматриваются алгоритмы кластеризации, которые обеспечивают получение оптимального решения в классе, меньшем класса всех возможных разбиений. Получающееся локально-оптимальное решение не обязательно будет оптимальным в классе всех разбиений.

Наиболее широкое применение получили алгоритмы последовательной кластеризации. В этих алгоритмах производится последовательный выбор точек-наблюдений и для каждой из них решается вопрос, к какому из m кластеров ее отнести. Эти алгоритмы не требуют памяти для хранения матрицы расстояний для всех пар объектов.

Остановимся на наиболее известной и изученной последовательной кластер-процедуре – методе k-средних (k-means). Особенность этого алгоритма в том, что он носит двухэтапный характер: на первом этапе в пространстве Е_n ищутся точки – центры клacтеров, а затем уже наблюдения распределяются по тем кластерам, к центрам которых они тяготеют. Алгоритм работает в предположении, что число m кластеров известно. Первый этап начинается с отбора m объектов, которые принимаются в качестве нулевого приближения центров кластеризации. Это могут быть первыеm из списка объектов, случайно отобранныеmобъектов, либо m попарно наиболее удаленных объектов.

Каждому центру приписывается единичный вес. На первом шаге алгоритма извлекается первая из оставшихся точек (пометим ее как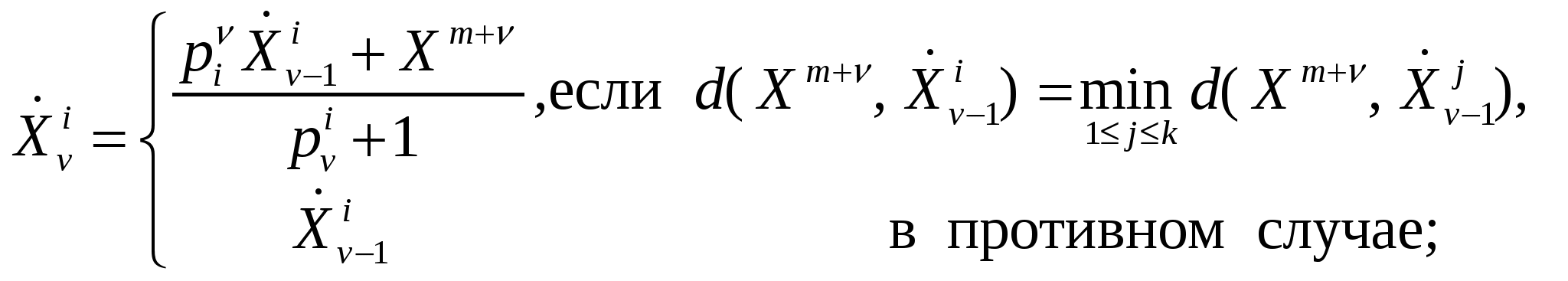) и выясняется, к какому из центров она оказалась ближе всего в смысле выбранной метрики d. Этот центр заменяется новым, определяемым как взвешенная комбинация старого центра и новой точки. Вес центра увеличивается на единицу. Обозначим через n-мерный вектор координат i-го центра на -м шаге , а через – вес этого центра. Пересчет координат центров и весов на -м шаге при извлечении очередной точки осуществляется следующим образом:
(9.5)
(9.6)
При достаточно большом числе классифицируемых объектов имеет место сходимость векторов координат центров кластеризации к некоторому пределу, то есть, начиная с некоторого шага, пересчет координат центров практически не приводит к их изменению.

Если в конкретной задаче устойчивость не имеет места, то производят многократное повторение алгоритма, выбирая в качестве начального приближения различные комбинации из m точек.

После того как центры кластеризации найдены, производится окончательное распределение объектов по кластерам: каждую точку , i=1,2,…, N относят к тому кластеру, расстояние до центра которого минимально.

Описанный алгоритм допускает обобщение на случай решения задач, для которых число кластеров заранее неизвестно. Для этого задаются двумя константами, одна из которых называется мерой грубости, а вторая Ψ₀ – мерой точности.

Число центров кластеризации полагается произвольным (пусть ), а за нулевое приближение центров кластеризации выбирают произвольные точек. Затем производится огрубление центров заменой двух ближайших центров одним, если расстояние между ними окажется меньше порога . Процедура огрубления заканчивается, когда расстояние между любыми центрами будет не меньше . Для оставшихся точек отыскивается ближайший центр кластеризации, и если расстояние между очередной точкой и ближайшим центром окажется больше, чем Ψ₀, то эта точка объявляется центром нового кластера. В противном случае точка приписывается существующему кластеру, координаты центра которого пересчитываются по правилам, аналогичным (9.5), (9.6).

20. Иерархический кластерный анализ. Проблема индексации.

Наряду с обычным, «раздельным», кластерным анализом широко применяется иерархический кластерный анализ, цель которого состоит в получении всей иерархии разбиений, а не отдельного разбиения. Считается, что иерархия точнее характеризует размытую структуру данных, чем отдельное разбиение. Получить конкретное разбиение в случае необходимости сравнительно легко сечением графа иерархий.

Основные определения Пусть О = {O¹, O², …,O^N} – конечное множество объектов. Иерархией h на О называется система подмножеств (классов) {K: KO}такая, что

1. 
   O h;
   
2. 
   {Oⁱ} h, i=1,2,…,N;
   
3. 
   для пересекающихся подмножества K и K´, т.е. KK´ ≠ Ø, KK´ либо K´K.
   

Пример. Пусть О = {О¹, О²,…, О⁵}. Тогда система подмножеств

h = {{O¹}, {O²}, …,{O⁵}, {O¹,O²}, {O³,O⁴}, {O¹,O²,O⁵}, O}

является иерархией на О.

Иерархия может быть представлена на языке теории графов. Графом иерархии h на О называется ориентированный граф (V,E), вершины vV которого соответствуют множествам Kh , а ребра eE– парам (K´,K), таким что K´K. Ребро e = (K´,K) изображается стрелкой с началом K´ и концом K.

Иерархической классификацией данного множества объектов

О = {O¹, O², …,O^N} называется построение иерархии h на О, отражающей наличие однородных в определенном смысле классов.

Если использовать неориентированный граф, то его структура становится деревом. Сам процесс классификации есть построение иерархического дерева исследуемой совокупности объектов. Графическое изображение неориентированного графа иерархии на плоскости называют дендрограммой.

В иерархическом кластерном анализе используются два вида алгоритмов: дивизимные и агломеративные. В дивизимных алгоритмах множество О постепенно делится на все более мелкие подмножества, в агломеративных – наоборот: точки множества О постепенно объединяются во все более крупные подмножества. Соответственно графы иерархий, полученные при помощи этих алгоритмов, называют дивизимными и агломеративными. Дивизимные алгоритмы называют также нисходящими (движение против стрелок на графе иерархии), агломеративные – восходящими (движение вдоль стрелок). Если на каждом шаге такого алгоритма объединяются только два кластера, то говорят о бинарном агломеративном алгоритме. Далее рассматриваются лишь такие алгоритмы.

Более подробно схема работы бинарного агломеративного алгоритма выглядит следующим образом. Исходное множество О = ={O¹, O², …,O^N} рассматривается как множество одноэлементных кластеров; выбирают два из них, например K_i и K_j, которые наиболее близки в смысле введенной метрики друг другу и объединяют их в один кластер. Новое множество кластеров будет иметь уже
N-1 элемент K₁,K₂,…,{K_i,K_j},…,K_N..

Рассматривая полученное множество в качестве исходного и повторяя процесс, получают последовательные множества кластеров, состоящие из N-2,N-3 и т.д. кластеров.

К достоинствам иерархических процедур относят полноту анализа структуры исследуемого множества наблюдений, возможность наглядной интерпретации проведенного анализа, возможность остановки процедуры при достижении априори заданного числа кластеров. К cущественным недостаткам иерархических процедур следует отнести финальную неоптимальность. Как правило, даже подчиняя каждый шаг работы процедуры некоторому критерию качества разбиения, получающееся в итоге разбиение для любого наперед заданного числа кластеров оказывается весьма далеким в смысле того же самого критерия качества.
21. Графическое представление результатов кластерного анализа.

Иерархическая классификация, как уже отмечалось, допускает наглядную интерпретацию. Для того чтобы привязать граф иерархии или дендрограмму к системе прямоугольных координат, введем понятие индексации. Индексацией  иерархии называется отображение : hR¹, ставящее в соответствие множеству Kh число (K)R¹ таким образом, что

1. 
    (K) = 0 для одноэлементных множеств K, т.е. K = 1;
   
2. 
    (K´) < (K) для каждой пары (K´,K) такой, что K´K, K´≠  K.
   

Индексация иерархии позволяет алгоритмизировать процесс построения дендрограммы. Пусть (h,ν) – некоторая индексированная иерархия h на множестве О = {O¹, O², …,O^N}. Вершины графа иерархии, отвечающие одноэлементным множествам {Oⁱ}, i = 1,2, …, N, обозначим через ν_i, а вершины, соответствующие К (К > 1), обозначим ν_К. Введем систему координат с осью абсцисс х и осью ординат η. Вначале на оси х через равные интервалы  размещаются вершины 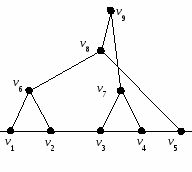, то есть представляются в виде точек с координатами = (i, 0). Предположим далее, что вершины и уже нанесены на плоскость в виде точек с координатами и . Тогда кластер K = K_iK_j может быть представлен точкой с координатами с последующим соединением ее с точками и . Напомним, что η _К > max(,) согласно п.2 определения индексации, так что вершина v_К расположится выше вершин и . Заметим, что построенная таким образом дендрограмма может содержать нежелательные пересечения ребер, поэтому вершины переупорядочиваются так, чтобы ребра соединялись только в вершинах. На рис.9 представлены дендрограммы иерархии с пересечением и без. Заметим также, что традиционно ребра диаграммы изображают в виде вертикальных и горизонтальных отрезков, как на дендрограмме без пересечений (рис.9,б).



а) б)

Рис.9. Дендрограммы иерархии примера из п.9.5.1:

а − с пересечением ребер; б − без пересечения ребер
Способы задания индекса ν могут быть разные. Весьма распространена индексация, ставящая в соответствие множеству Kh номер шага, на котором это множество было включено в иерархию. В качестве альтернативы индексом может выступать мощность множества, точнее ν = K – 1.

Информативность дендрограммы существенно возрастает, если в качестве ординаты кластера K, полученного объединением кластеров K_i и K_j, т.е. K = K_iK_j, выступает расстояние между кластерами d(K_i, K_j). Такое изображение называют оцифрованным.

Одна из проблем иерархического кластерного анализа – определить, какие метрики позволяют провести оцифрование, удовлетворяющее условиям индексации, или иначе, найти индексацию, такую что ν(К_iК_j) = d(К_i,К_j). Так, для евклидовой метрики ответ на этот вопрос – отрицательный, что можно проиллюстрировать следующим примером. Пусть пять двумерных объектов, подлежащих кластеризации, образуют конфигурацию, представленную на рис.10, а.

а )

б)

Рис.10. Пример инверсии для евклидовой метрики:

а − исходная конфигурация; б − инверсия
На первом шаге агломеративной процедуры получаем кластер К₁=.{О¹,О²} c координатами центра тяжести Z(К₁) = (1,5;1). Для кластера К₁, полученного объединением одноэлементных кластеров {O¹} и{O²}, d(О¹, О²) = 1. Ближайшимк К₁ окажется объект О³ (точнее одноэлементный кластер К₂={O³}) с координатами центра тяжести v(К₂)= (1,5; ). На следующем шаге алгоритма образуется, очевидно, кластер К₃=К₁К₂ с d(К₁, К₂) = (1 – )², поскольку расстояние между кластерами измеряется по центрам тяжести (квадрат евклидова расстояния). Выходит для кластера К₃ потенциальный индекс, равный расстоянию (1–)², оказывается меньше по сравнению с индексом К₁, равным 1. Налицо инверсия, поскольку нарушено требование 2, предъявляемое к индексам: К₁ К₃ν(К₁) < ν(К₃)(см. рис.10, б).

Достаточные условия, когда оцифрование является и индексацией, содержатся в теореме Миллигана. Эта теорема опирается на рекуррентную формулу Жамбю, которая позволяет пересчитывать расстояния между имеющимся кластером К и вновь образованным K=K_iK_j(KK_i, KK_j), используя расстояния и индексы, полученные на предыдущих шагах: d(K, K) = a₁d(K,K_i)+a₂d(K,K_j)+a₃d(K_i,K_j)+a₄ν(K)+

+a₅ν(K_i)+a₆ν(K_j)+a₇d(K, K_i)–d(K,K_j),

где a_i – числовые коэффициенты, зависящие от метода определения расстояния между кластерами. Так, при

а₁=а₂=–а₇=1/2 и а₃=а₄=а₅=а₆=0

приходим к расстоянию, измеренному по принципу «ближайшего соседа», а при

а₁=а₂=а₇=1/2 и а₃=а₄=а₅=а₆=0 – «дальнего соседа».

Теорема Миллигана. Пусть h – иерархия на О, полученная с использованием метрики d(К₁,К₂), для которой справедлива формула Жамбю. Тогда, если а₁+а₂+а₃1, а_j0дляj=1,2,4,5,6 и а₇–min(а₁,а₂),

то отображение , задаваемое формулой (К₁К₂) = =d(К₁,К₂) и условием ν({Оⁱ})=0, i=1,2, …,N, является индексацией.

В заключение отметим, что если рассечь дендрограмму горизонтальной линией на некотором уровне *, получаем ряд непересекающихся кластеров, число которых равно количеству «перерезанных» линий (ребер) дендрограммы; состав кластера определяется терминальными вершинами, связанными с данным «перерезанным» ребром.
22. Многомерное шкалирование. Метрический и неметрический подходы.

Кроме таблиц «объект-признак» источником данных могут служить таблицы «объект-объект», содержащие данные о связях объектов. Математический образ подобных таблиц – квадратная матрица, элемент которой на пересечении i-й строки и j-го столбца содержит сведения о попарном сходстве либо различии анализируемых объектов. Задача состоит в том, чтобы представить эти объекты в виде точек некоторого координатного пространства невысокой размерности. При этом связи объектов должны быть переданы расстояниями между точками. Такая простая геометрическая модель приводит к содержательно интерпретируемому решению: каждая ось порождаемого пространства является одномерной шкалой и соответствует некому латентному признаку. Тем самым объекты наделяются признаками, интерпретация которых связывается с расположением объектов в искомом пространстве.

Формальная постановка задачи шкалирования

Дана симметричная матрица различий между объектами .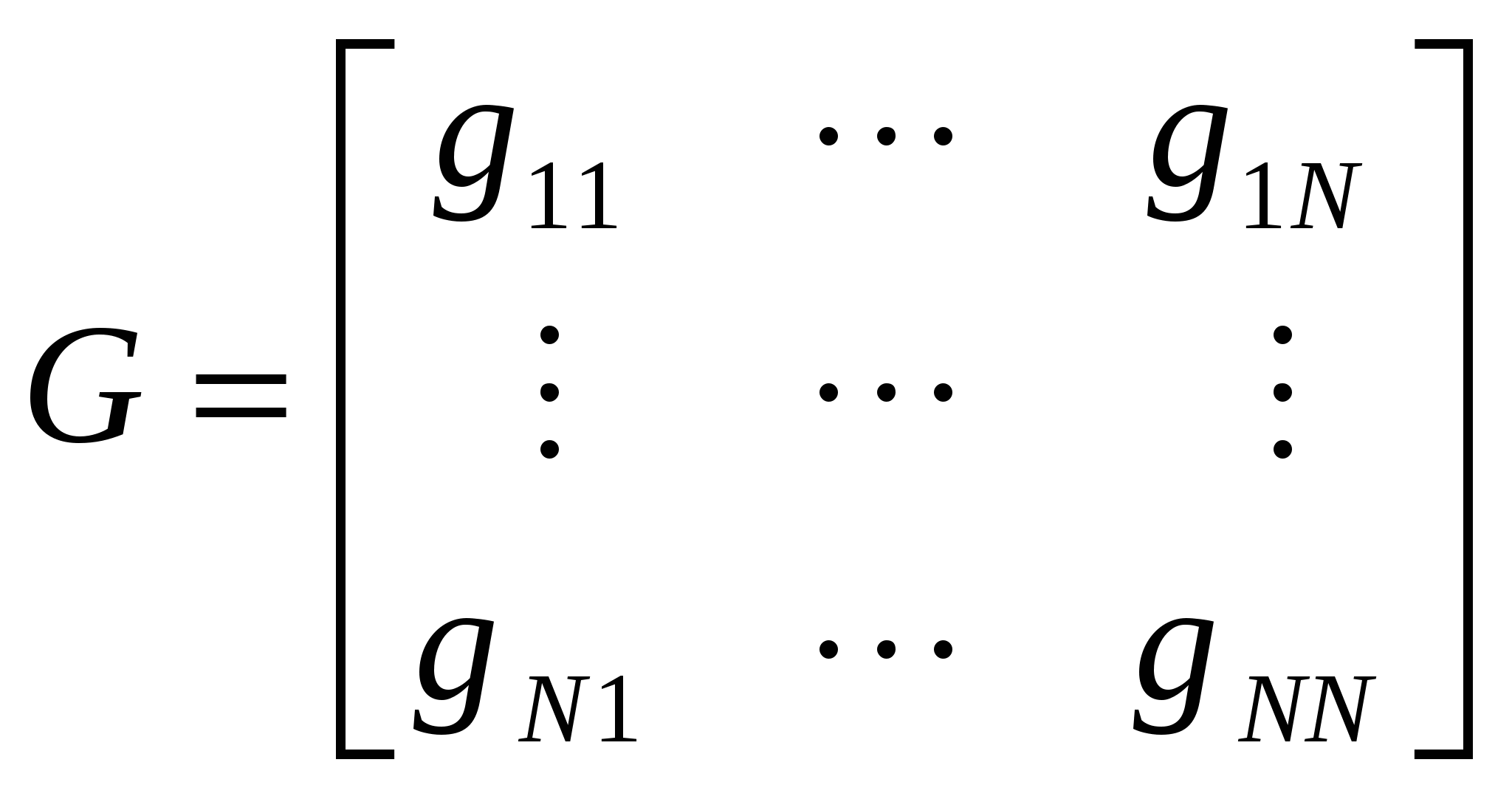

Требуется построить пространство возможно меньшей размерности r и найти в нем координаты точек-объектов

так, чтобы матрица расстояний

между ними, вычисленная по введенной на Х метрике, была, в смысле некоторого критерия, близка к исходной матрице G попарных различий.

При решении поставленной задачи возможны два подхода: метрический, при котором матрица различий G изначально является искомой матрицей расстояний D, и неметрический (монотонный, ранговый), ориентированный на сохранение того же порядка попарных расстояний, что и в исходной матрице различий: → .

Неметрический этап

На этом этапе данные о различиях и стандартизированные оценки расстояний из предыдущей итерации используются для вычисления отклонений.

Этап состоит из нескольких шагов.

1. Упорядочить по возрастанию данные о различиях по исходной матрице G. Получившийся порядок пар объектов задает и порядок оценок расстояний или отклонений.

2. Серия проходов: в начале первого прохода на конкретной итерации отклонениями являются текущие оценки расстояний из предыдущей итерации или стартовой конфигурации. В начале каждого последующего прохода на той же итерации отклонения берутся из предыдущего прохода. Проход начинается с разбиения оценок отклонений на блоки равных значений. Пусть m=(1,...,M) будет индексом, обозначающим блоки от самого верхнего (m=1) до самого низкого (m=M). Начиная с m=1, элементы m-го блока сравниваются с элементами (m+1)-го блока. Если элементы m-го блока меньше элементов (m+1)-го блока, необходимо перейти к сравнению двух следующих блоков. Как только элементы m-го блока окажутся больше элементов (m+1)-го блока, то все элементы m-го и (m+1)-го блоков приравниваются среднему арифметическому обоих блоков. Эти два блока объединяют в один, который становится новым
m-ым блоком. Затем опять сравнивают m-й и (m+1)-й блоки; проход заканчивается после сравнения всех соседних блоков. Результат прохода – новый набор оценок отклонений. После завершения проходов отклонения будут удовлетворять условию монотонности (12.1). Пример работы алгоритма дается в табл.27.

Таблица 27

№ п/п	Различие	До объединения		После 1-го прохода		После 2-го прохода
		Откло- нение	Блок	Откло-нение	Блок	Откло-нение	Блок
1	2	3	4	5	6	7	8
1	0,19	0,11	1	0,11	1	0,11	1
2	0,22	0,12	2	0,12	2	0,12	2
3	0,23	0,16	3	0,15	3	0,15	3
4	0,25	0,14	4	0,15	3	0,15	3

Продолжение табл.27

№ п/п	Различие	До объединения		После 1-го прохода		После 2-го прохода
		Откло- нение	Блок	Откло-нение	Блок	Откло- нение	Блок
5	0,26	0.21	5	0.21	4	0.21	4
6	0,27	0,23	6	0,23	5	0,23	5
7	0,28	0,25	7	0,25	6	0,24	6
8	0,29	0,23	8	0,23	7	0,24	6
9	0,32	0.27	9	0.27	8	0,27	7

В столбце 3 нет подряд идущих одинаковых чисел, так что каждая строка образует блок. Просматривая этот столбец сверху вниз, обнаруживаем, что в строках 3 и 4 имеет место инверсия (нарушение монотонности –– 0,16>0,14). Блоки 3 и 4 объединяются в один со значением (0,16+0,14)/2=0,15. Просматривая теперь столбец 5, убеждаемся в необходимости слияния блоков 6 и 7. Как видно из 7-го столбца нарушений условия монотонности не осталось, что позволяет считать элементы столбца 7 искомыми отклонениями .

Метрический этап

На этом этапе решают задачу математического программирования, в результате чего получают новые оценки координат, по которым рассчитывают новые оценки расстояний. Исходными данными являются отклонения, рассчитанные на неметрическом этапе, оценки координат и расстояний предыдущей итерации. В качестве целевой функции выступает S₁ (12.2).

Минимизация S₁ проводится одним из градиентных методов.
23. Многомерное шкалирование. Теорема Янга-Хаусхолдера.
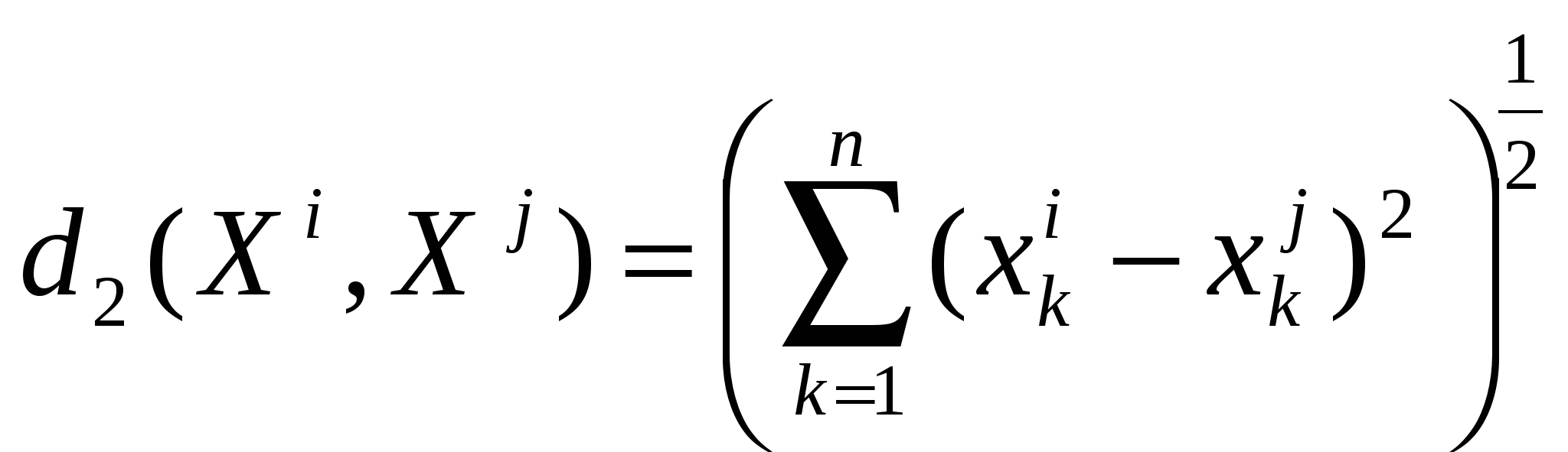