Анализ данных. Разложение суммы квадратов в однофакторном да
 Скачать 2.64 Mb. Скачать 2.64 Mb.
|
Метрическое шкалирование В метрическом шкалировании укажем два метода: ординация Орлочи и метод главных проекций Торгерсона.Ординация Орлочи представляет собой сравнительно простой геометрический метод. По матрице G вначале выбирают две наиболее различающиеся (удаленные) точки Прямая, проходящая через эти две точки, принимается за первую ось. Обозначим ее A1A2 (рис.15).  Рис.15. Ординация Орлочи Проекции (координаты) остальных точек на первую ось, как видно из рис. 15, составят Строится матрица расстояний по найденным координатам, которая сравнивается с матрицей различий. Если соответствие приемлемое, решение достигнуто; в противном случае необходимо искать вторую ось, проходящую через точку, наиболее удаленную от прямой Координаты остальных точек – проекции на полученные оси – можно получить геометрическим построением либо аналитически. Однако повышение размерности приводит к сложностям получения оценок. К тому же решение оказывается излишне чувствительным к данным, поскольку оно определяется всего по нескольким точкам. В методе главных проекций Торгерсона предполагается, что матрицаG – матрица евклидовых расстояний между объектами, не содержащая ошибок. По матрице G необходимо определить размерность пространства и проекции точек на его оси.Пусть 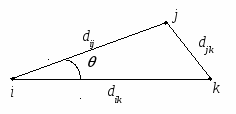 Рис. 16. Графическая иллюстрация скалярного произведения Вычислим симметричную матрицу Biразмерности N×Nс элементами bjk, представляющими скалярное произведение векторов с началом в точке i и концами в точках jи k: Любая из Nточек может быть взята в качестве i-й. Таким образом можно получить Nвозможных матриц Bi. Согласно теореме Янга-Хаусхолдера: 1. Если какая-либо Bi(i=1,2,…,n) является положительно полуопределенной (ППО), то различия между объектами можно рассматривать как расстояния между точками в вещественном евклидовом пространстве. 2. Ранг любой ППО матрицы соответствует размерности r множества точек. (Напомним, то ранг ППО матрицы равен числу положительных собственных значений.) 3. Любую ППО матрицу можно факторизовать в виде Bi=XX′. Элементы Х есть проекции точек-объектов на rортогональных осей в r-мерном вещественном пространстве с центром в точке i. Для того чтобы уменьшить влияние возможных ошибок, начало координат помещают в центр тяжести всех объектов. Тогда координаты искомых (центрированных) точек будут иметь вид: Матрица скалярных произведений Легко видеть, что Матрицу В алгоритме Торгерсона предполагается, что матрица различий является и матрицей расстояний, т.е. G = D. Это требование можно ослабить, допуская, что матрица различий может быть преобразована в матрицу расстояний с помощью аддитивной константы, т.е. D = G + C, где С – матрица, по главной диагонали которой стоят нули, а остальные элементы – одно и то же число с (аддитивная константа). Эта константа должна быть такой, чтобы разместить объекты в вещественном пространстве возможно меньшей размерности. Так, для матрицы 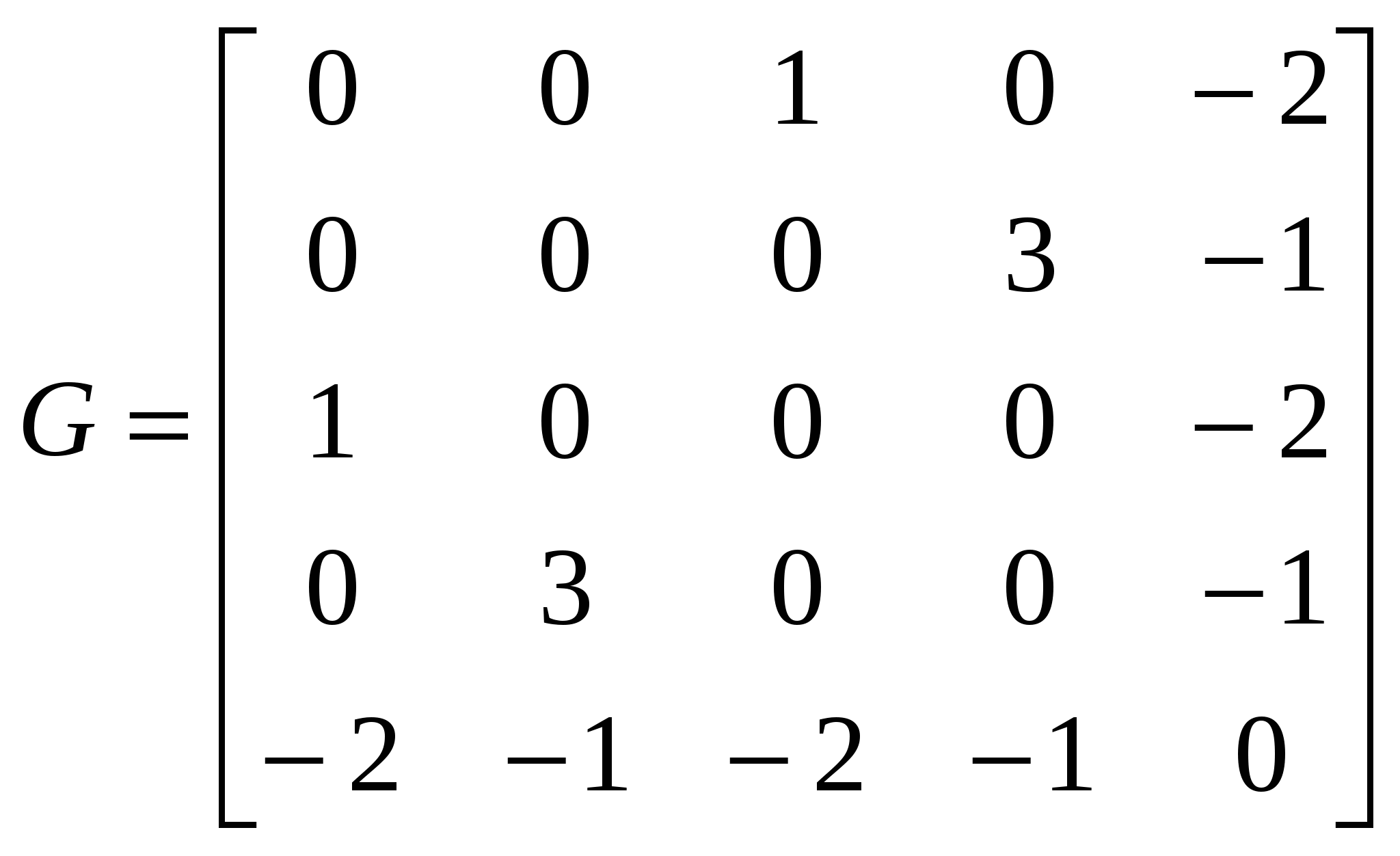 аддитивная константа есть с=5. аддитивная константа есть с=5. Преобразованная матрица 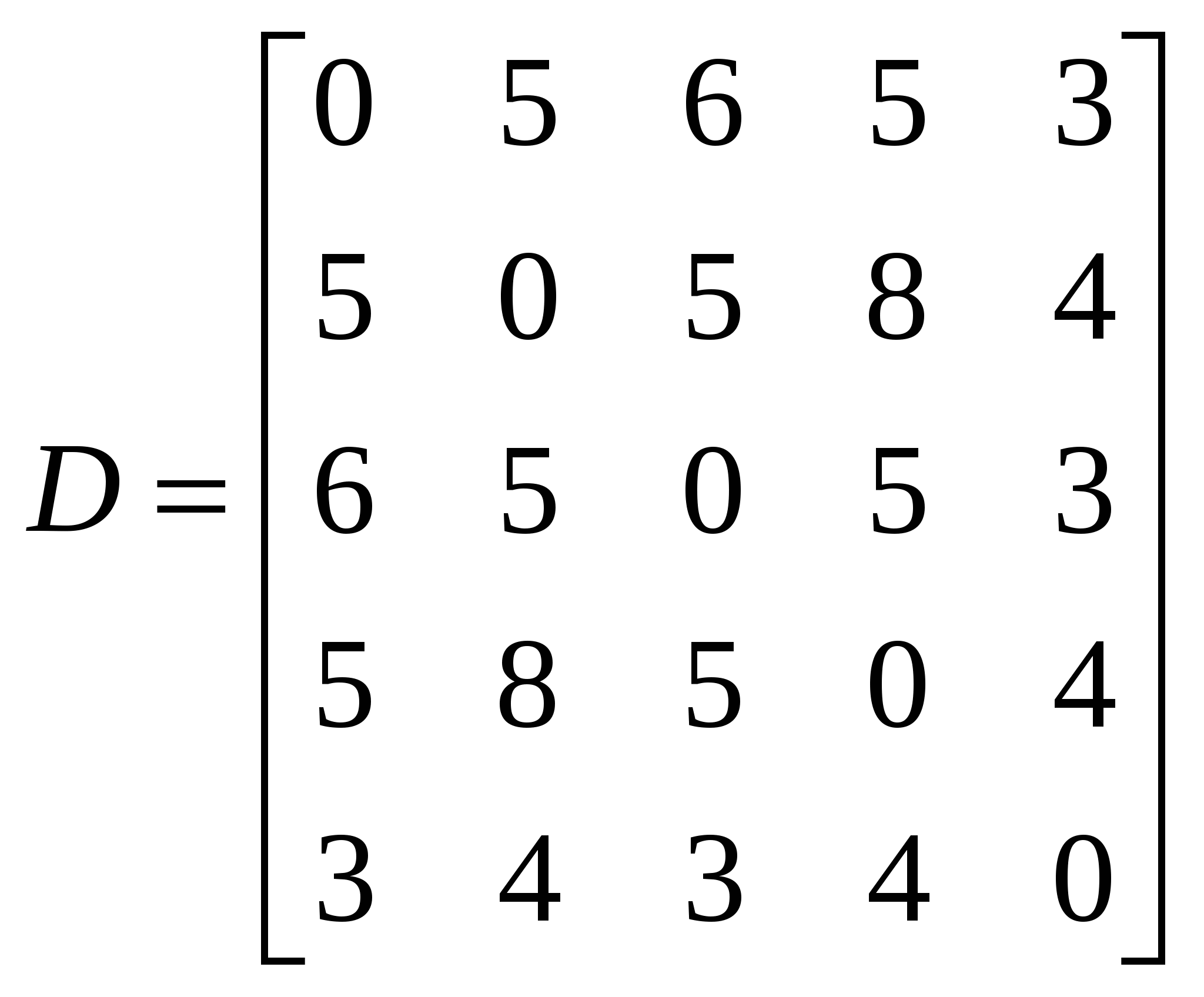 стала матрицей расстояний пяти точек на плоскости (рис.17). 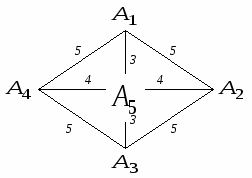 Рис.17. Конфигурация точек для матрицы расстояний D Отметим, что при с<5 разместить объекты в вещественном евклидовом пространстве невозможно (не выполняется правило треугольника), при с>5 размерность превышает 2. 24. Ортогональные методы многомерного шкалирования. В метрическом шкалировании укажем два метода: ординация Орлочи и метод главных проекций Торгерсона. Ординация Орлочи представляет собой сравнительно простой геометрический метод. По матрице G вначале выбирают две наиболее различающиеся (удаленные) точки Прямая, проходящая через эти две точки, принимается за первую ось. Обозначим ее A1A2 (рис.15).  Рис.15. Ординация Орлочи Проекции (координаты) остальных точек на первую ось, как видно из рис. 15, составят Строится матрица расстояний по найденным координатам, которая сравнивается с матрицей различий. Если соответствие приемлемое, решение достигнуто; в противном случае необходимо искать вторую ось, проходящую через точку, наиболее удаленную от прямой Координаты остальных точек – проекции на полученные оси – можно получить геометрическим построением либо аналитически. Однако повышение размерности приводит к сложностям получения оценок. К тому же решение оказывается излишне чувствительным к данным, поскольку оно определяется всего по нескольким точкам. В методе главных проекций Торгерсона предполагается, что матрицаG – матрица евклидовых расстояний между объектами, не содержащая ошибок. По матрице G необходимо определить размерность пространства и проекции точек на его оси.Пусть  Рис. 16. Графическая иллюстрация скалярного произведения Вычислим симметричную матрицу Biразмерности N×Nс элементами bjk, представляющими скалярное произведение векторов с началом в точке i и концами в точках jи k: Любая из Nточек может быть взята в качестве i-й. Таким образом можно получить Nвозможных матриц Bi. Согласно теореме Янга-Хаусхолдера: 1. Если какая-либо Bi(i=1,2,…,n) является положительно полуопределенной (ППО), то различия между объектами можно рассматривать как расстояния между точками в вещественном евклидовом пространстве. 2. Ранг любой ППО матрицы соответствует размерности r множества точек. (Напомним, то ранг ППО матрицы равен числу положительных собственных значений.) 3. Любую ППО матрицу можно факторизовать в виде Bi=XX′. Элементы Х есть проекции точек-объектов на rортогональных осей в r-мерном вещественном пространстве с центром в точке i. Для того чтобы уменьшить влияние возможных ошибок, начало координат помещают в центр тяжести всех объектов. Тогда координаты искомых (центрированных) точек будут иметь вид: Матрица скалярных произведений Легко видеть, что Матрицу 25. Неметрическое шкалирование. Схема алгоритма Каскала. Рассмотрим один из известных алгоритмов неметрического многомерного шкалирования, предложенный Дж. Краскалом. Пусть Для оценки степени расхождения вводят меру соответствия (S-стресс): 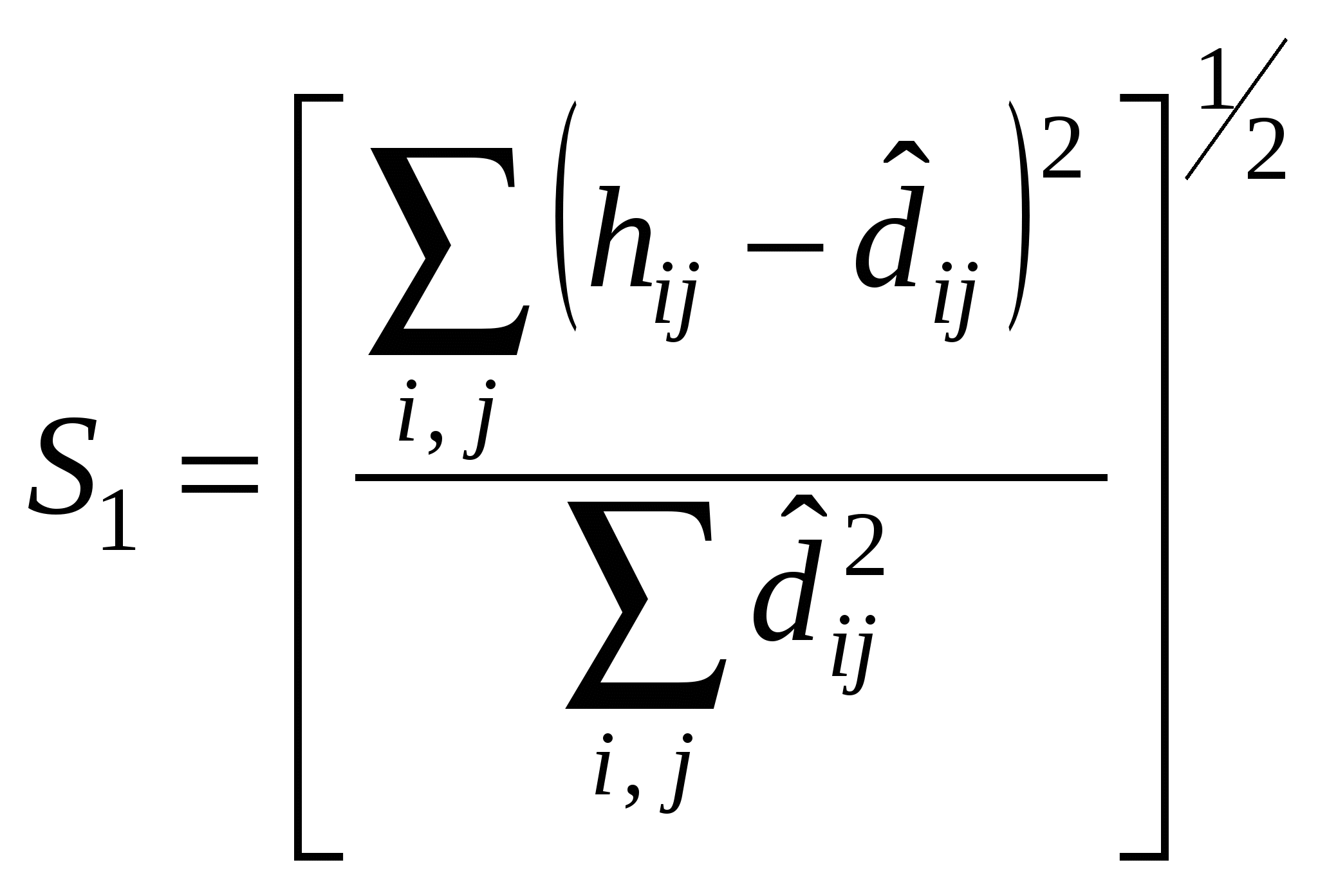 либо либо 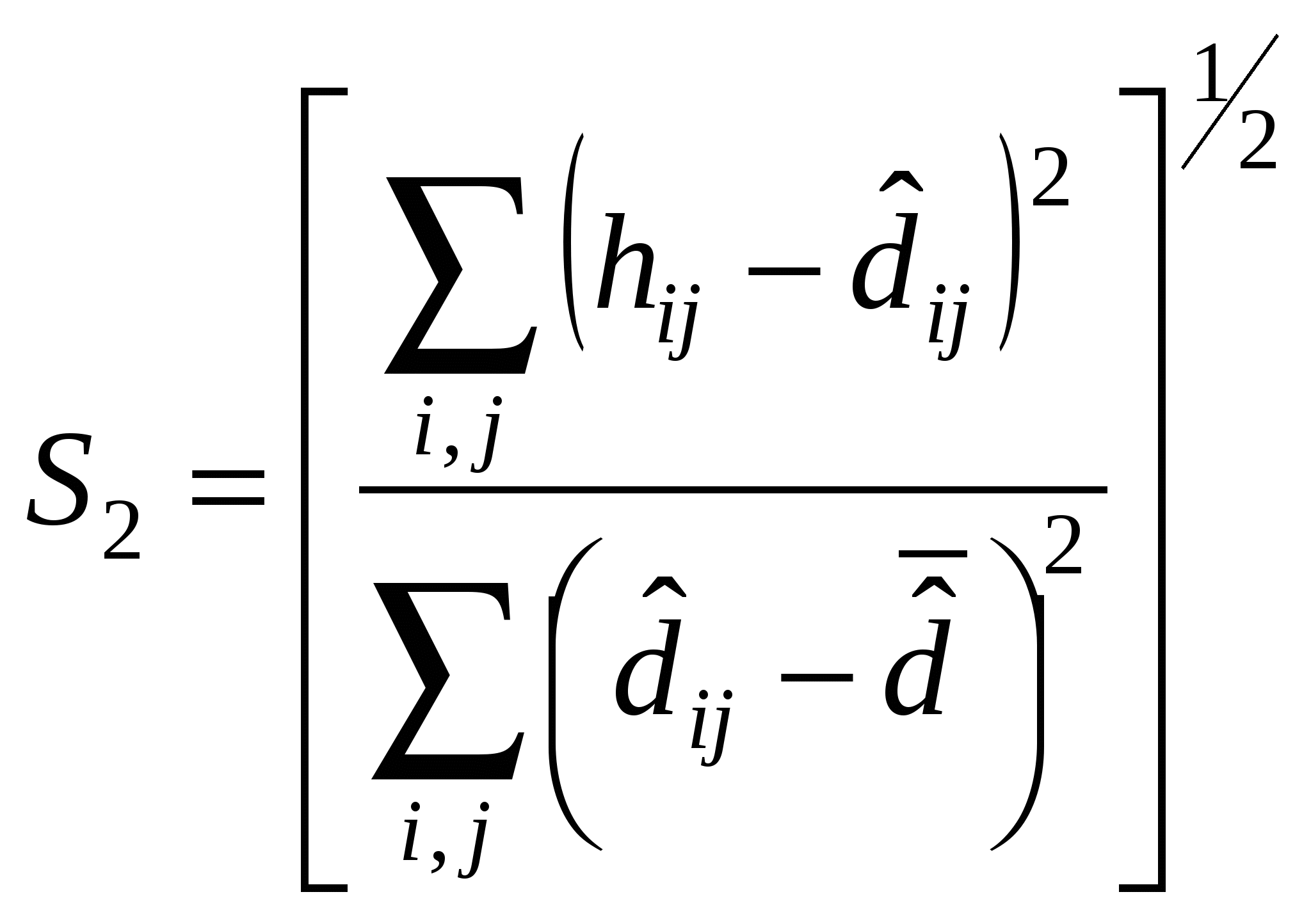 , где , где Наряду с S-стрессом используется SS-стресс, где в числителе оценки расстояний и отклонения заменены их квадратами. SS-стресс обеспечивает более быструю сходимость, если матрица различий симметрична. Алгоритм Краскала состоит из пяти основных этапов: 1) формирование стартовой конфигурации, то есть получение начальных оценок координат (размерность пространства предполагается известной); 2) стандартизация расстояний и оценок координат; 3) неметрический этап, в ходе которого вычисляются отклонения; 4) метрический этап: перерасчет оценок координат; 5) подсчет меры соответствия. Если мера улучшилась, то возвращаются к этапу 2; в противном случае работа алгоритма завершается. Рассмотрим перечисленные этапы подробнее. Стартовая конфигурация строится по методу Торгерсона (ортогональное проектирование). Затем по координатам найденных точек вычисляется матрица расстояний с элементами На втором этапе в ходе первой итерации текущие расстояния и координаты – те, которые получены из стартовой конфигурации. Для всех итераций, кроме первой, в качестве текущего расстояния и оценок используются те, что были получены на метрическом этапе предыдущей итерации. Стандартизация оценок расстояний и координат состоит в делении их на сумму квадратов 26. Критерии качества шкалирования. |
