Анализ данных. Разложение суммы квадратов в однофакторном да
 Скачать 2.64 Mb.
|
Последовательный симплексный метод Этот метод требует проведения минимально возможного числа опытов при определении направления движения.Симплексом в n-мерном пространстве называют многогранник с (n+1)-й вершиной. Если расстояния между вершинами симплекса одинаковы, такой симплекс называют регулярным. Симплексный метод включает в себя следующие основные процедуры: 1. Линейное преобразование входных переменных с таким расчетом, чтобы изменение каждой из них на единицу одинаково сказывалось бы на изменении выходной переменной. 2. Построение регулярного симплекса и реализация опытов в вершинах симплекса. 3. Отбрасывание вершины с минимальным значением целевой величины и построение нового симплекса, который образуется оставшимися вершинами исходного симплекса и новой вершиной, получаемой зеркальным отображением отброшенной вершины относительно противоположной ей  -мерной грани исходного симплекса. Координаты этой новой вершины рассчитываются по формуле:  , где  − номер отброшенной вершины.4. Проведение эксперимента в вершине  и возврат к п. 3. Если оказывается, что выходная переменная в новой вершине приняла значение меньшее, чем в остальных вершинах симплекса, то следует возвратиться к предыдущему симплексу. Во избежание зацикливания в качестве отбрасываемой выбирают вершину, в которой выходная переменная имеет величину, следующую по порядку за наихудшей вершиной симплекса. Аналогично следует поступать, если новая вершина выходит за пределы симплекса.5. Если при перемещении симплекса за 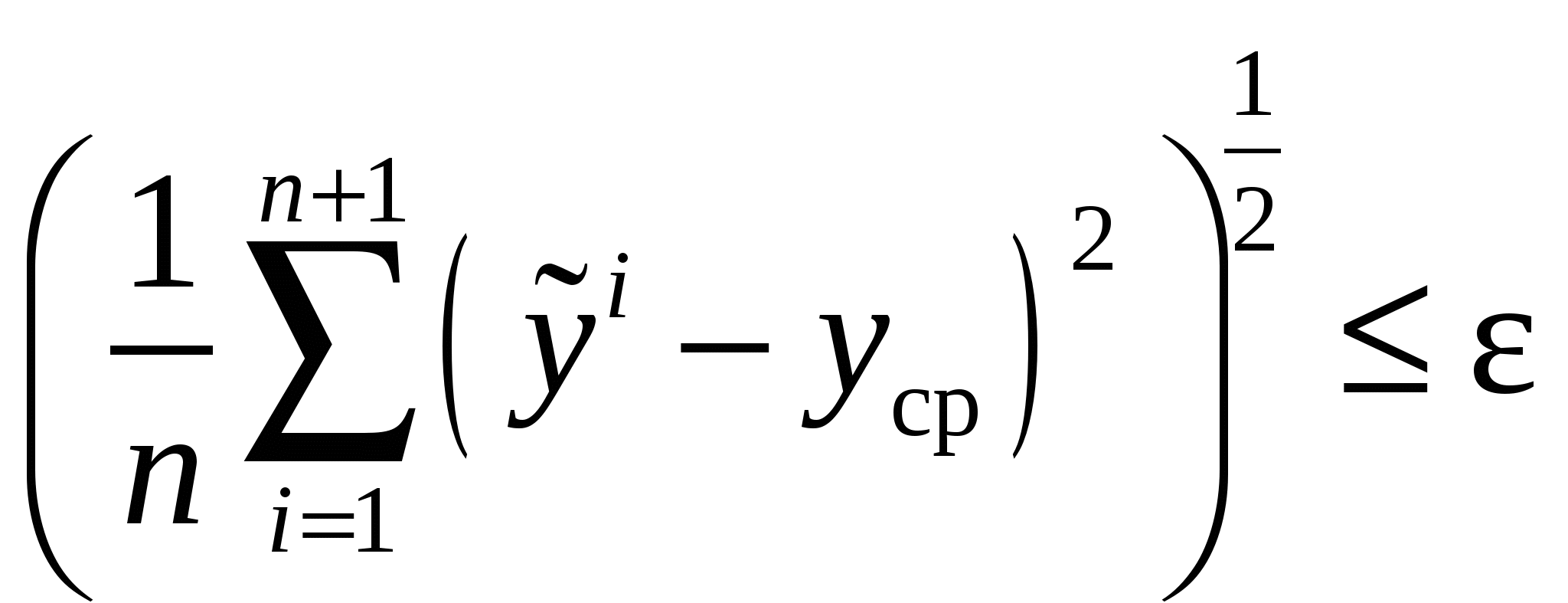 шагов некоторая вершина сохраняет свое положение, то симплекс совершит оборот относительно этой вершины. Это означает достижение области оптимума. Другим условием достижения оптимума является выполнение неравенства: , где – малая величина (порог),  – среднее значение выходной величины в вершинах симплекса.К числу достоинств симплексного метода наряду с экономичностью по числу опытов и простотой вычислений следует отнести также возрастание эффективности метода с ростом числа входных переменных, устойчивость выделения направления движения, поскольку оно определяется только соотношением целевых величин, а не их абсолютными значениями. Графическая иллюстрация симплексного метода при двух входных переменных приведена на рис.5. Здесь поверхность отклика задается линиями уровня. x2 x1 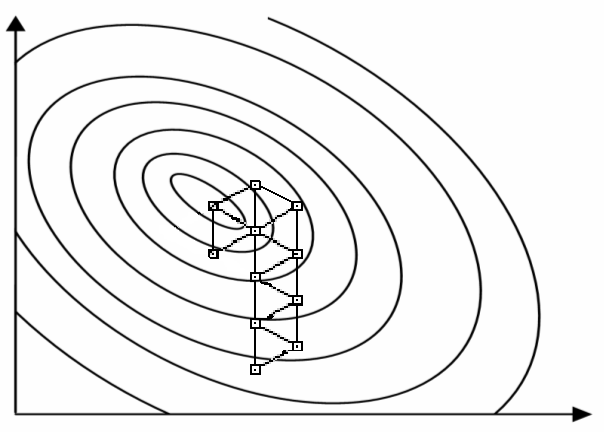 Рис. 5. Схема последовательного симплексного метода 13. Метод Бокса-Уилсона. На основе малой серии опытов строится линейное описание поверхности отклика в окрестности начальной точки. В центре этой локальной области определяется значение градиента, после чего начинаются опыты в направлении градиента. Бокс и Уилсон предложили использовать дробные факторные планы для поиска линейной модели. Метод состоит из последовательности циклов, каждый из которых содержит два шага. 1. Построение линейной модели в окрестности некоторой начальной точки  с использованием подходящего факторного плана. Окрестность начальной точки, определяемая интервалами варьирования переменных, должна быть не слишком малой, чтобы можно было выявить линейные эффекты на фоне случайных возмущений, и не настолько большой, чтобы обеспечить адекватность линейного приближения. Соотношение между интервалами варьирования  по отдельным переменным должно быть таким, чтобы величины коэффициентов регрессии в случае их значимости имели бы одинаковый порядок. В случае адекватности линейной модели  коэффициенты регрессии  совпадают с компонентами градиента, т.е.   , где i, j,…,k – направляющие векторы осей координат. Обычно переходят к нормированному градиенту делением его компонент на норму  либо просто на  . Компоненты нормированного градиента обозначим  .2. Пошаговое увеличение величины целевой функции (движение в направлении градиента). Координаты точки наблюдения на  -м шаге при движении в направлении градиента определяются по формуле: , где  ≥1 – параметр, позволяющий управлять величиной шага, а следовательно, скоростью движения. Чем ближе исследователь подходит к стационарной области, тем меньше . Движение в направлении градиента продолжается до тех пор, пока возрастают значения выходной переменной. В противном случае вновь реализуют факторный план, находят новое линейное приближение и цикл повторяется снова. Если же модель оказывается неадекватной, то это означает, что исследователь либо достиг стационарной области, либо необходимо линейную модель дополнить взаимодействиями. В стационарной области метод Бокса−Уилсона неработоспособен, здесь необходимо переходить к квадратичным моделям. Геометрическая интерпретация метода приведена на рис.4. Здесь поверхность отклика задается линиями уровня. x2  x1 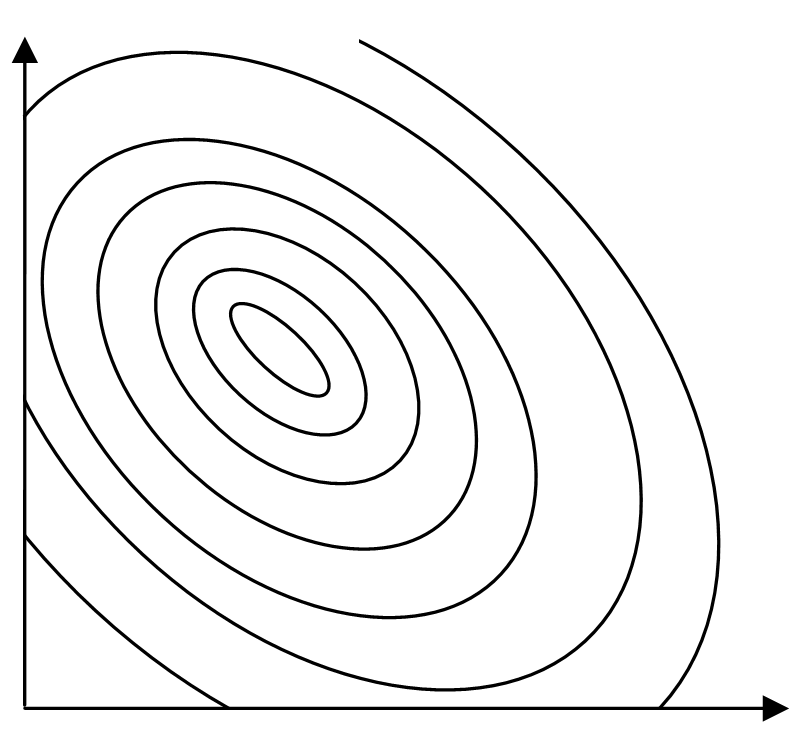 Рис. 4. Схема метода Бокса–Уилсона Рассмотрим в качестве примера использование метода Бокса−Уилсона для поиска максимума функции  . (6.11)Допустимая область изменения переменных: 0х120, 0х210, 1х315. Начальная точка поиска х0=  =(3,2,4). Линейное приближение будем строить в окрестности начальной точки, задаваемой условиями:  , i=1,2,3. Значения i желательно подбирать такими, чтобы приращения функции по каждому из аргументов были сопоставимы, то есть   . Примем 1=1, 2=2, 3=3. В соответствии с (6.1) стандартизованная переменная  , если  , и  при  .Линейная модель  требует для своей оценки не менее четырех экспериментов. Воспользуемся ДФЭ 23-1 с ГС:  (табл. 16).Таблица 16
В последнем столбце табл.16 содержатся значения функции (6.11) для исходных переменных, то есть 40,8=у(4,4,7) и так далее. МНК-оценки коэффициентов линейной модели составят:  ;  ;  .Отнормируем полученные компоненты градиента, поделив их на максимальное значение  :  b1=3,4/4,3=0,79, b2=1, b3=0,91. Движение в направлении градиента представлено в табл.17. Таблица 17
Движение в направлении градиента после четвертого шага невозможно из-за ограничения на х3. Теперь следует определить градиент в точке x0+3bii. Поскольку темп роста функции замедлился на последних шагах, область линейного описания следует сузить, уменьшив значения i. 14. Анализ главных компонент. Вычислительная процедура. Пусть имеется множество, состоящее из N объектов. Каждый объект описывается с помощью n переменных (признаков, факторов). Совокупность значений переменных сведена в матрицу: 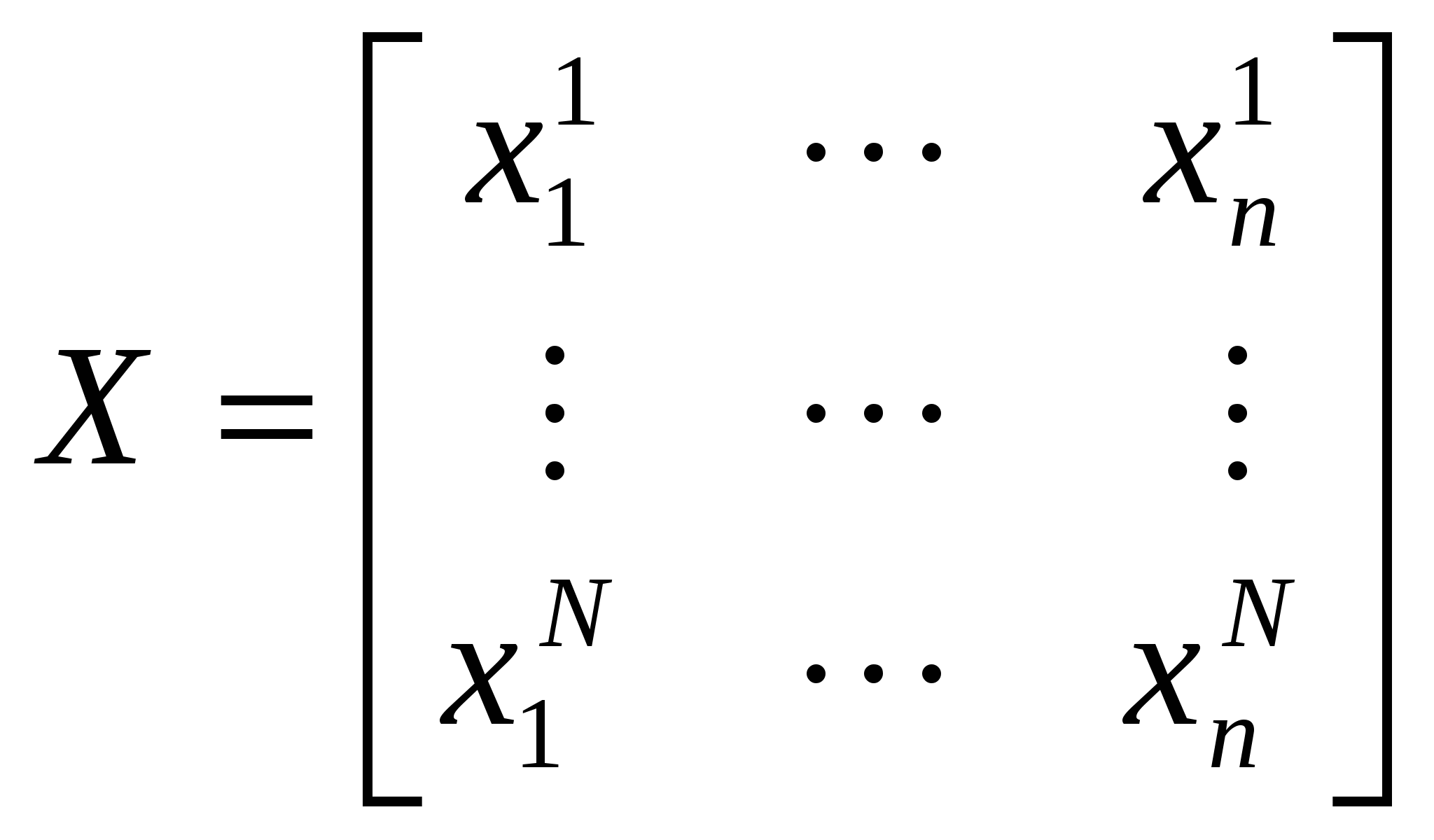 , (10.1)в которой наблюдения представлены в виде отклонений от выборочных средних, иначе говоря, центрированы, т.е.  ,  , где  – среднее значение j-й переменной,  – результат измерения j-го признака на i-м объекте. От исходного вектора признаков  перейдем к новому множеству переменных  .Каждую компоненту вектора z будем представлять в виде некоторой линейной комбинации исходных признаков, т.е.  , j=1,2,…,n, (10.2)где  – вектор искомых весовых коэффициентов.На компоненты вектора z наложим следующее требование: первая переменная  должна быть ориентирована по направлению максимально возможной дисперсии, вторая − по направлению максимально возможной дисперсии в подпространстве, ортогональном первому направлению, и т.д. Компоненты вектора z, удовлетворяющие этому требованию, называют главными компонентами.Вычисление главных компонент Вычисление весовых коэффициентов будем проводить последовательно, начиная с первой главной компоненты. Значение первой главной компоненты для i-го объекта (i=1,2,…,N) составит  . (10.3) Вводя векторное обозначение  , выражение (10.3) можно записать в виде  . (10.4)Оценка дисперсии D(z1) центрированной переменной есть по определению среднее квадрата ее значений. Таким образом,  . (10.5) есть не что иное, как оценка матрицы ковариаций исходных признаков  . Эту оценку обозначим  . Выражение (10.5) примет вид:  . (10.5а)Вектор параметров  необходимо подобрать так, чтобы дисперсия D(z1) была максимальной. Если на параметры не накладывать никаких ограничений, то, очевидно, такая задача не имеет конечного решения. Потребуем, чтобы норма (длина) вектора , равнялась единице:  . (10.6)Для максимизации (10.5а) при ограничении (10.6) воспользуемся методом неопределенных множителей Лагранжа. Определим  ,где  – множитель Лагранжа.Дифференцирование  по отдельным элементам вектора компактно может быть записано так: . Полагая  , получаем  . (10.7)Из (10.7) видно, что – собственный вектор матрицы , соответствующий собственному значению λ1. Из (10.6) и (10.7) следует, что  .Поскольку  максимизируется, в качестве  выбирается наибольшее собственное значение матрицы  .При поиске значений элементов вектора  , кроме ограничения на норму вектора, аналогичного (10.6), требуется обеспечить ортогональность векторов значений первой и второй главных компонент  и  . Так как скалярное произведение ортогональных векторов равняется нулю, а матрица симметричная и, следовательно,  , то справедлива следующая цепочка равенств:  .Поскольку ни (N-1), ни нулю не равны, имеем:  . (10.8)Определим функцию Лагранжа следующим образом:  ,где λ2 и  – множители Лагранжа.Приравняем нулю частную производную φ по  :  .Умножая последнее равенство слева на  и принимая во внимание условие нормировки (10.6), получаем:  .Учитывая, что  , а также условие (10.8), имеем:  .Следовательно, соотношение (10.8) примет вид  ,где в качестве  выбирается второе по величине собственное значение матрицы  . Этот процесс продолжается до тех пор, пока не исчерпается список всех n собственных значений матрицы . Полученные в результате n собственных векторов матрицы составят ортогональную матрицу:  .В итоге, значения главных компонент задаются матрицей:  .Ковариационная матрица главных компонент есть  .Введем диагональную матрицу собственных значений 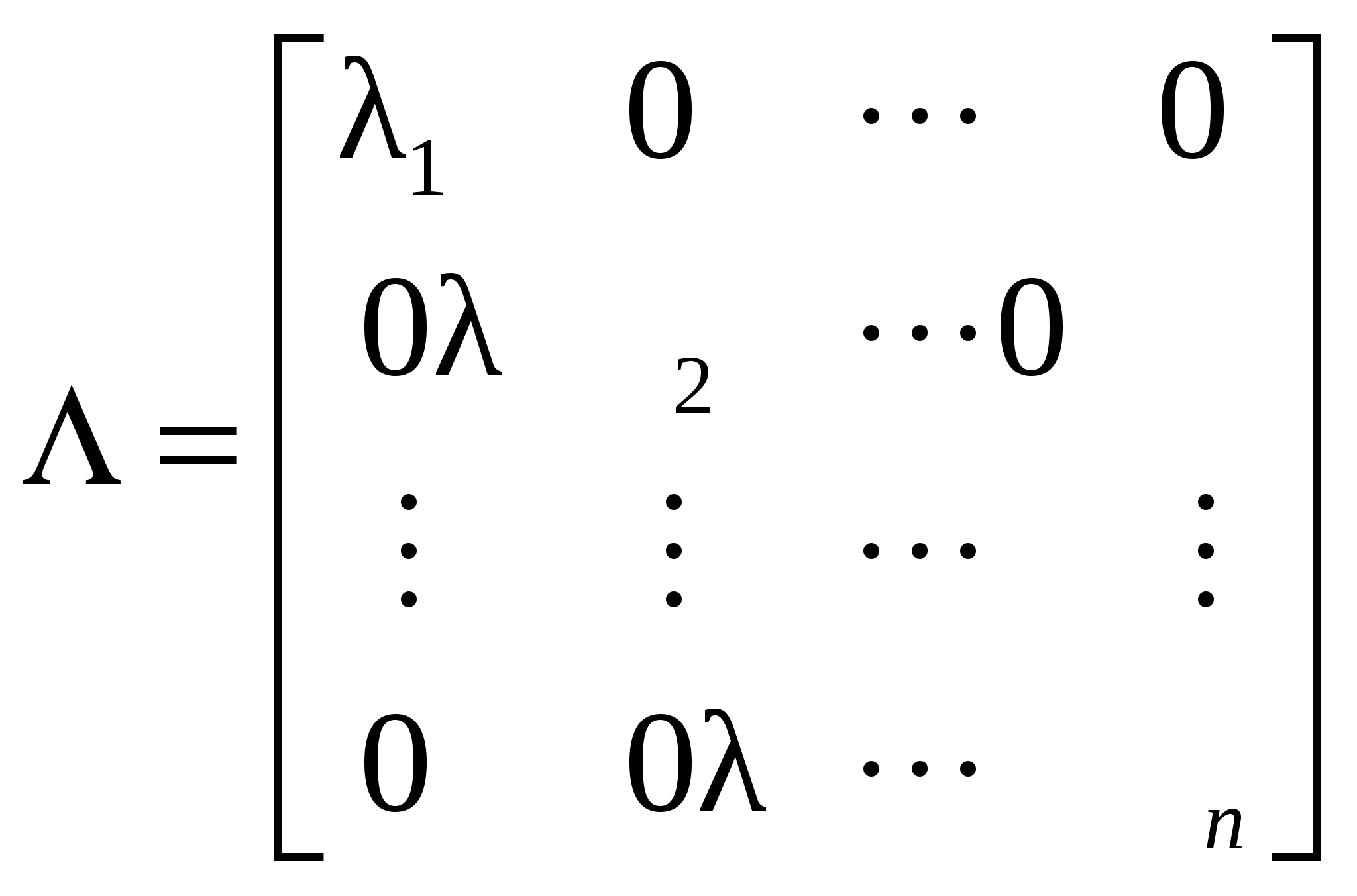 Тогда  , и окончательное выражение для ковариационной матрицы главных компонент приобретает вид  , поскольку  в силу ортогональности собственных векторов.Следовательно, главные компоненты попарно некоррелированы, а их дисперсии совпадают с собственными значениями ковариационной матрицы исходных переменных. Если ранг матрицы Х меньше n , то у матрицы будет k нулевых собственных значений, и изменения в переменных могут быть полностью выражены с помощью n-k независимых переменных. При отсутствии нулевых собственных значений некоторые  могут оказаться весьма близкими к нулю, так что существенный вклад в суммарную дисперсию будут вносить первые несколько главных компонент.Суммарная дисперсия исходных переменных, равная следу матрицы , равняется суммарной дисперсии главных компонент. Действительно,  .Здесь мы воспользовались свойством неизменности следа произведения матриц при перестановке сомножителей, т.е. tr(AB)=tr(BA) (предполагается, что произведение ВА существует). Тогда отношения 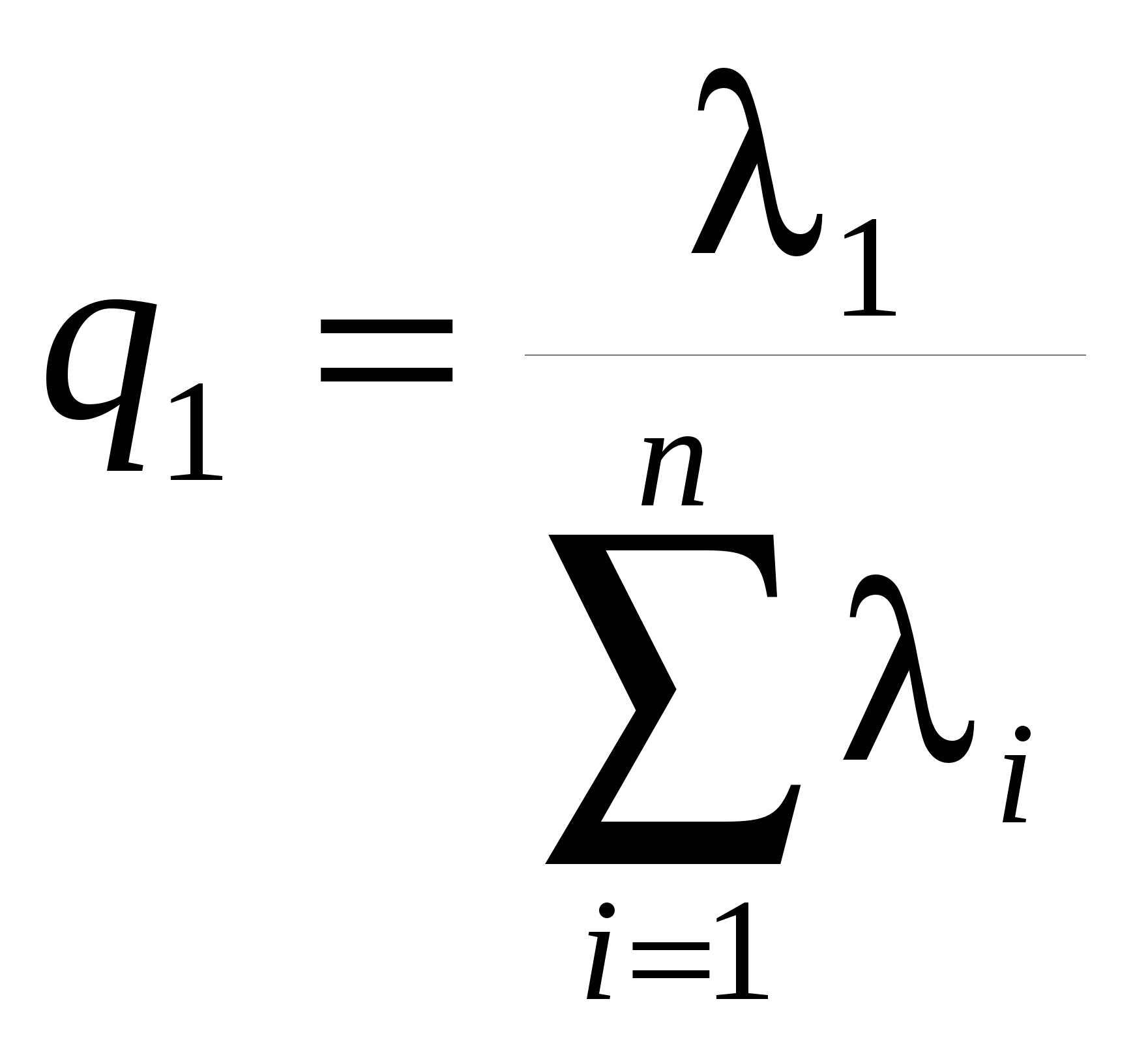 , ,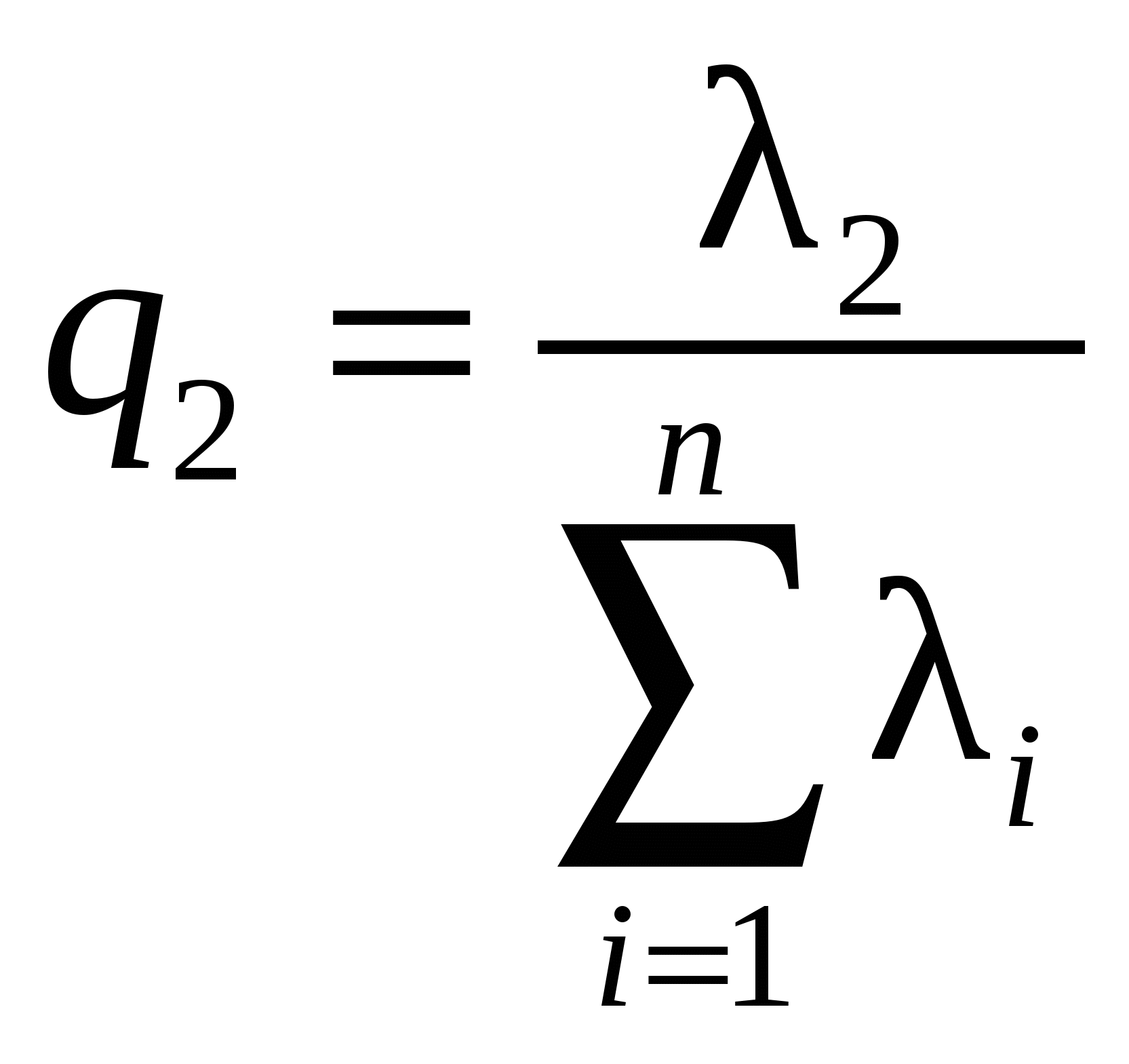…, ,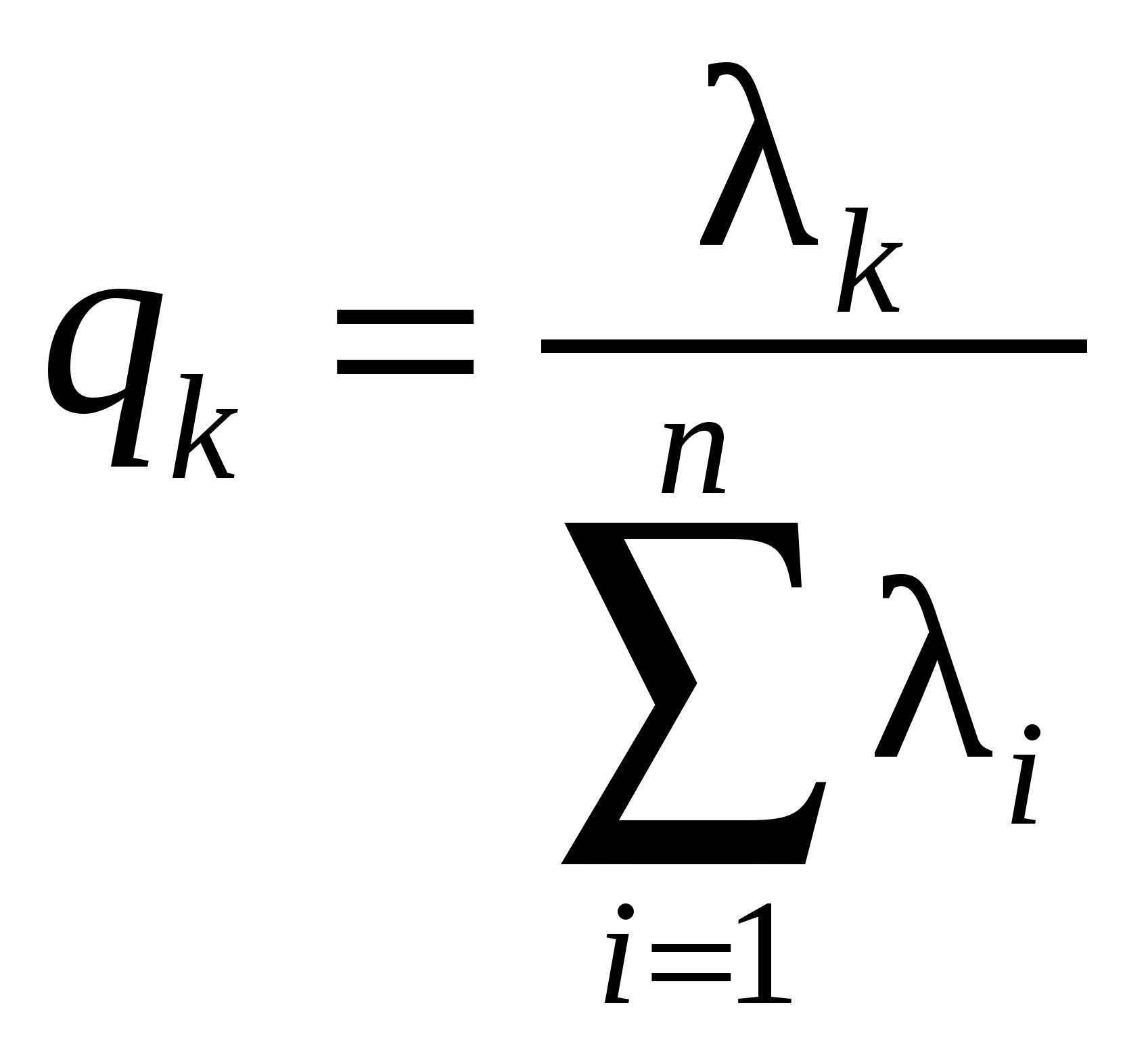 характеризуют пропорциональный вклад каждого вектора, представляющего главные компоненты, в суммарную дисперсию исходных переменных. Накопленные отношения  показывают относительную долю в суммарной дисперсии исходных переменных, которая приходится на первые k главных компонент. Задавшись некоторым порогом  , для дальнейшего анализа оставляют те первые k΄ главных компонент, для которых  .В заключение сделаем два замечания. 1. Переход к главным компонентам наиболее естественен и эффективен, когда исходные признаки имеют общую физическую природу и измерены в одних и тех же единицах. Если это условие не имеет место, то результаты иcследования с помощью главных компонент будут существенно завиcеть от выбора масштаба и природы единиц измерения. В качестве практического средства в таких ситуациях можно рекомендовать переход к вспомогательным безразмерным признакам  нормированием исходных признаков  по формуле  где  – дисперсия i-го признака.2. Аналитически доказано, что переход от исходного n-мерного пространства к m-мерному пространству главных компонент сопровождается наименьшими искажениями суммы квадратов расстояний между всевозможными парами точек наблюдений, расстояний от точек наблюдений до их общего центра тяжести, а также углов между прямыми, соединяющими всевозможные пары точек наблюдений с их общим центром тяжести | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||