Анализ данных. Разложение суммы квадратов в однофакторном да
 Скачать 2.64 Mb. Скачать 2.64 Mb.
|
В п.4.2 рассматривался вопрос включения в регрессию качественных переменных. В случае, когда регрессорами являются только качественные переменные, общепринятым методом исследования выступает дисперсионный анализ (ДА). В зависимости от числа регрессоров, называемых в ДА факторами, говорят об одно-, двух-, многофакторном ДА. Сами факторы полагаются неслучайными (модель с постоянными эффектами) либо случайными (модель со случайными эффектами). В модели с постоянными эффектами речь идет в основном о сравнении средних значений количественной переменной при различных значенииях факторов, тогда как в моделях со случайными эффектами интересует доля изменчивости, вносимая отдельными факторами. Ниже рассматривается первая модель, для которой ДА часто называют одно-, двух-, многофакторной классификацией. Однофакторный дисперсионный анализ Имеется количественная переменная у, определяемая качественной переменной, иначе фактором, принимающим р дискретных значений (уровней). Так, фактором может быть «поставщик», уровнями – определенные фирмы-поставщики, переменной у– срок службы поставляемого товара. В качестве исходных данных выступает выборка, содержащая ряд наблюдений на каждом из уровней (по нескольку экземпляров определенного товара от каждого поставщика). Необходимо ответить на вопрос – различаются ли по сроку службы объекты от разных поставщиков. Модель однофакторного анализа: где Модель (5.1) не позволяет однозначно оценить параметры, поскольку можно добавить к m и вычесть из ai произвольную константу. Неоднозначность снимается условием репараметризации N1a1+N2a2+…+Npap=0. (5.2) Оценивание параметров производится по методу наименьших квадратов (МНК). Для минимизации остаточной суммы квадратов Обозначим 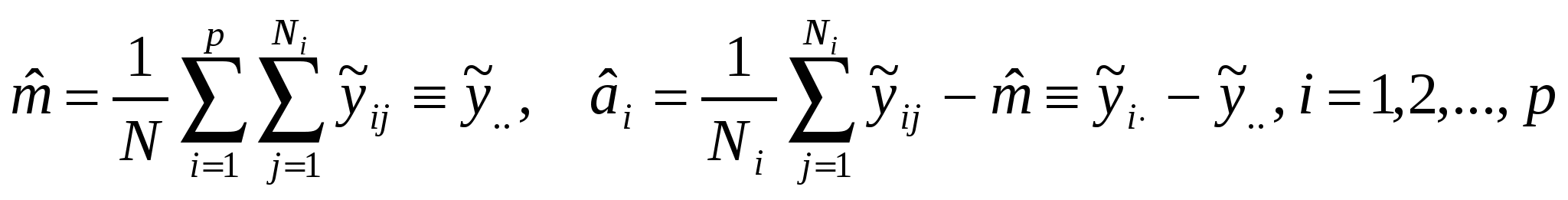 . (5.3) . (5.3)(Точка на месте индекса означает усреднение по этому индексу.) Результаты измерений принято представлять в виде табл.11. Таблица 11
В ДА основной интерес представляет не столько сами оценки, сколько их сравнение и, в первую очередь, проверка гипотезы Н0: а1=а2=…=ар=0, означающей одинаковость, неразличимость, воздействий всех р уровней. Со статистической точки зрения задачу ДА можно сформулировать так: для каждой из р генеральных совокупностей получено по выборке объемом Ni и необходимо сопоставить р значений выборочных средних. ДА базируется на разложении общей суммы квадратов S0 отклонений наблюдений 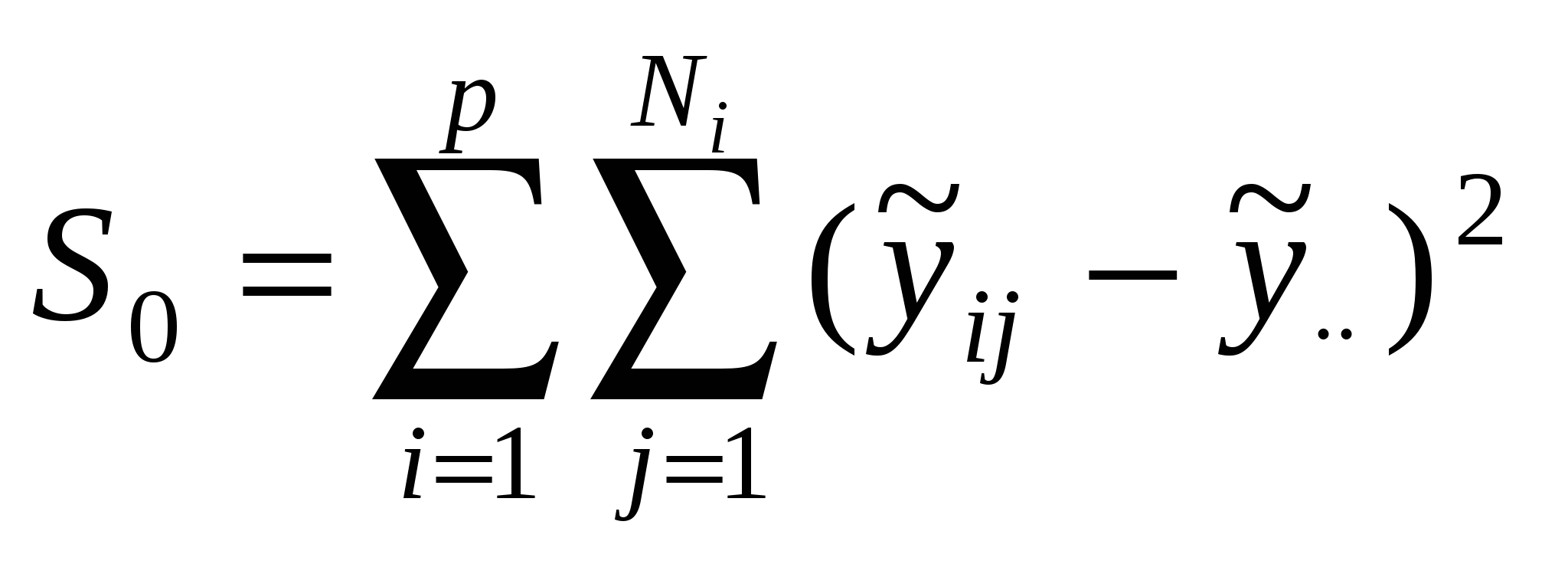 , Sму= , Sму=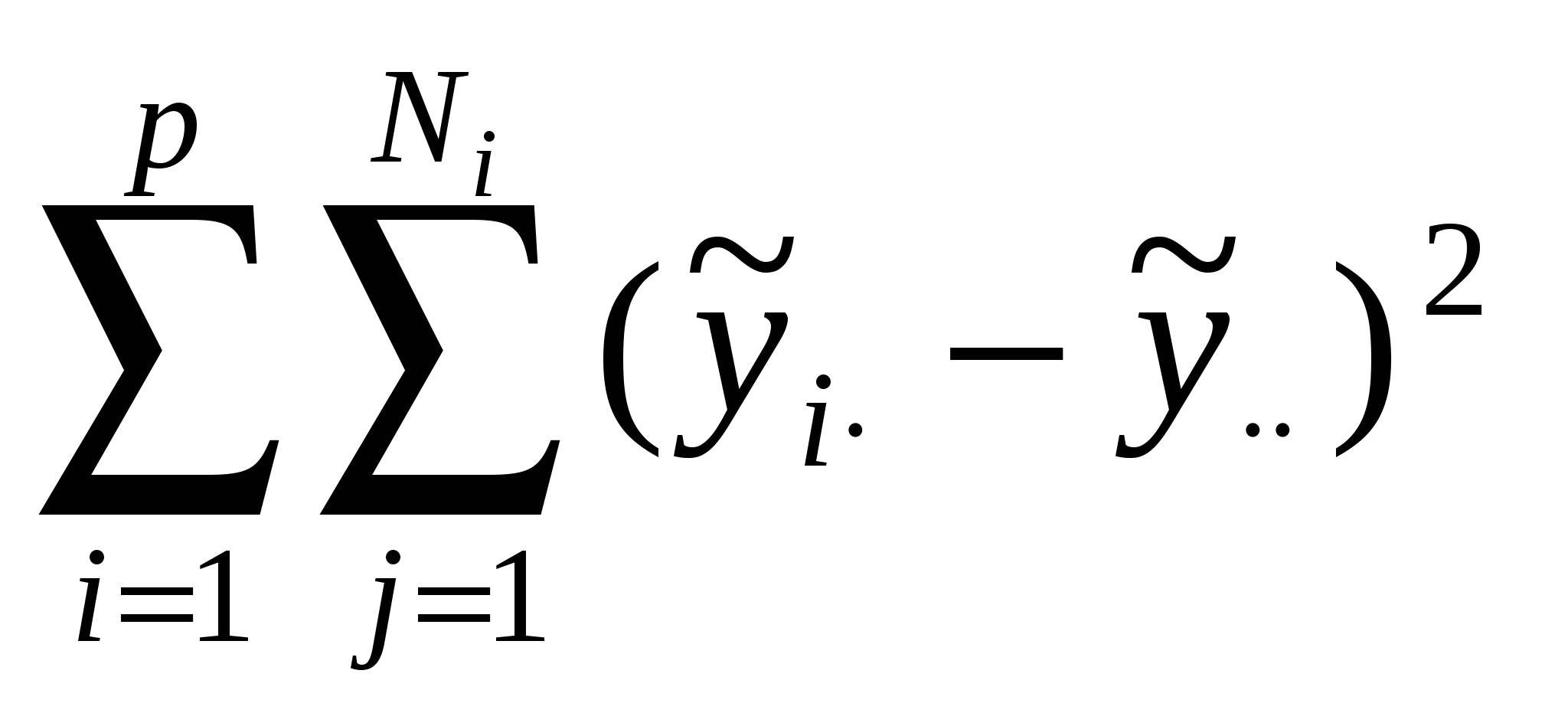 ,Sву= ,Sву=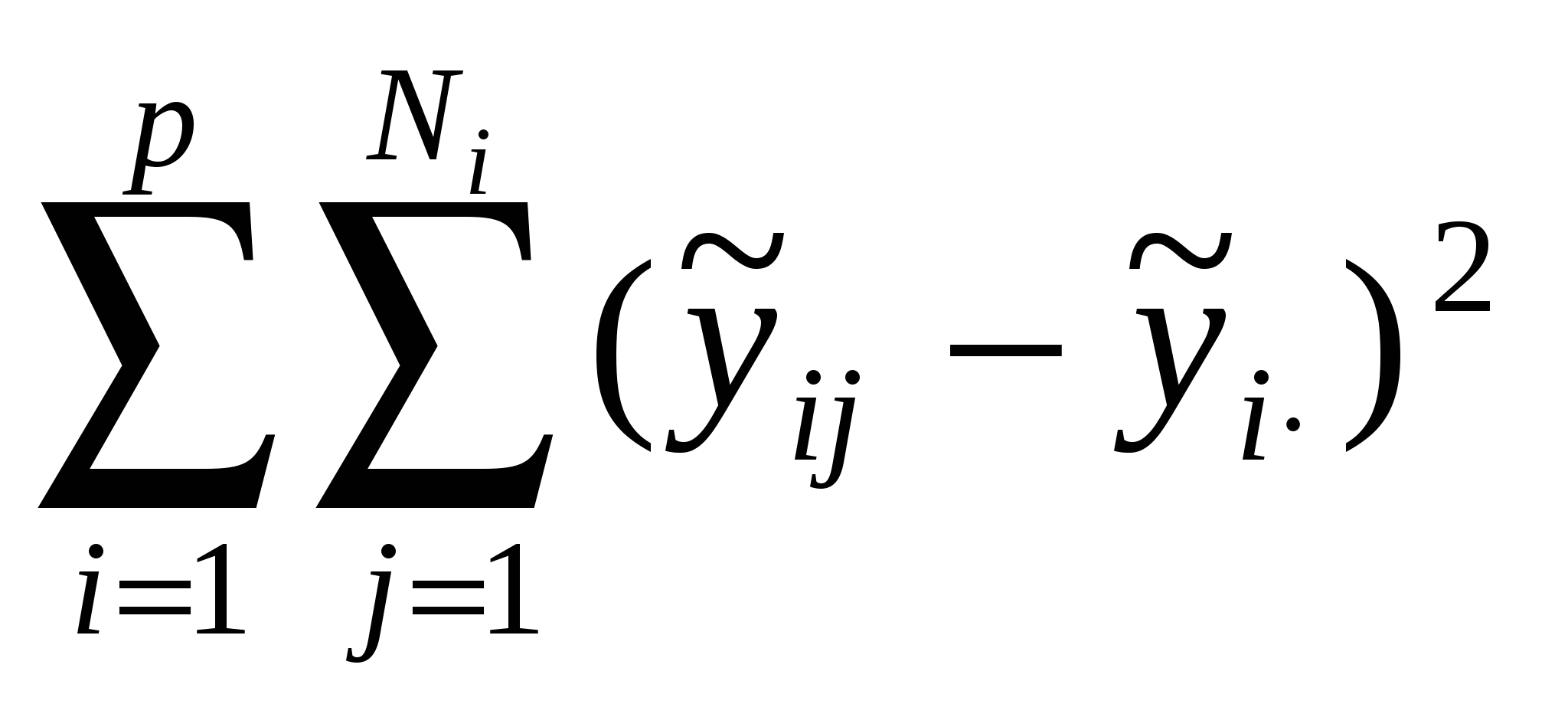 . .Подобное разложение получается следующим образом. Обе части тождества 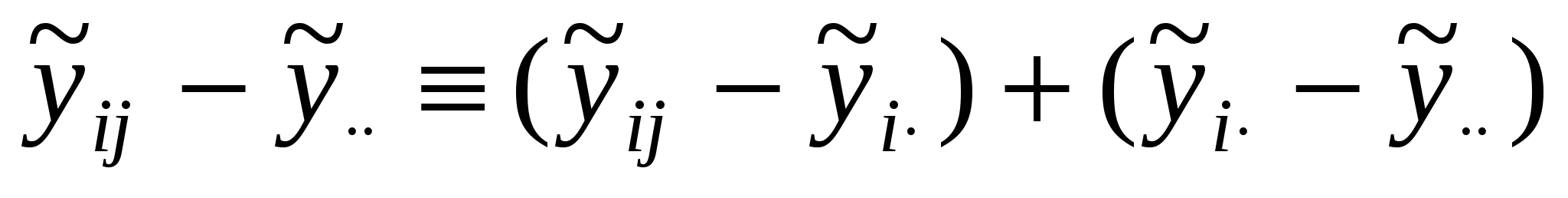 возводят в квадрат и суммируют по i и j: 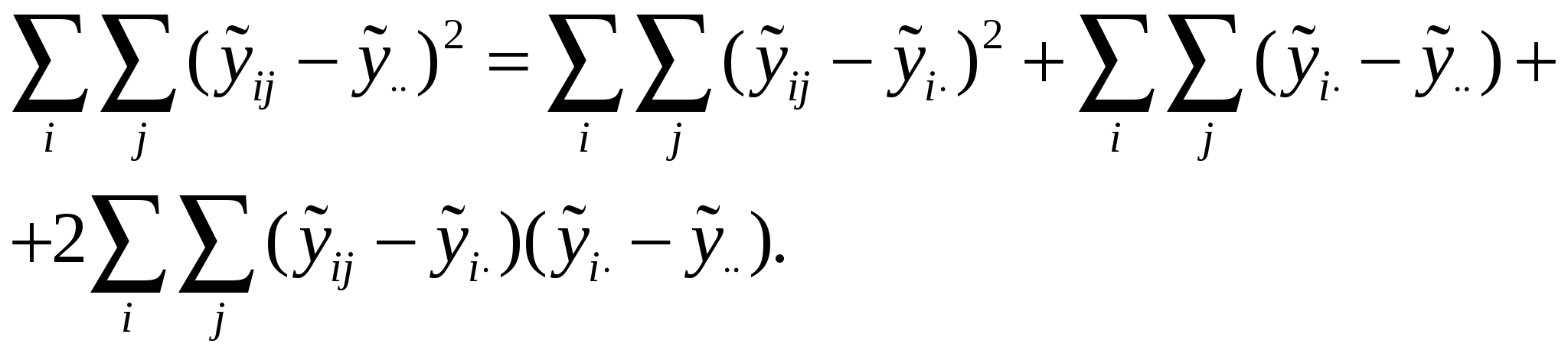 (5.4) (5.4)Последнее слагаемое в правой части формулы (5.4) обращается в нуль в силу выполнения следующей очевидной цепочки равенств: 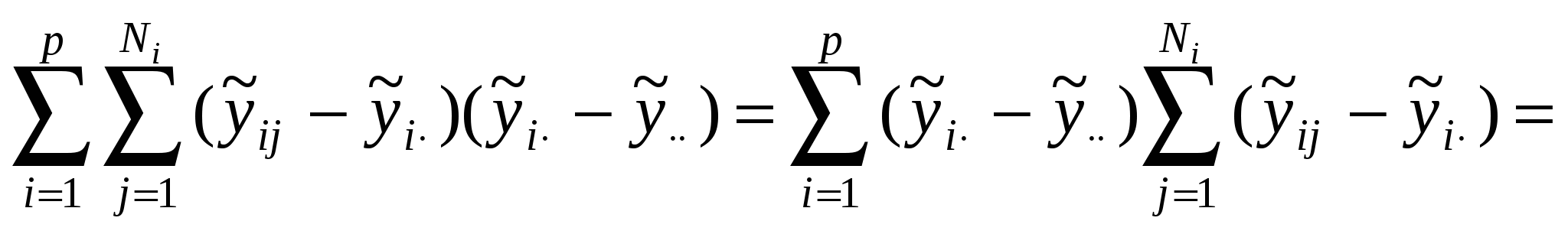 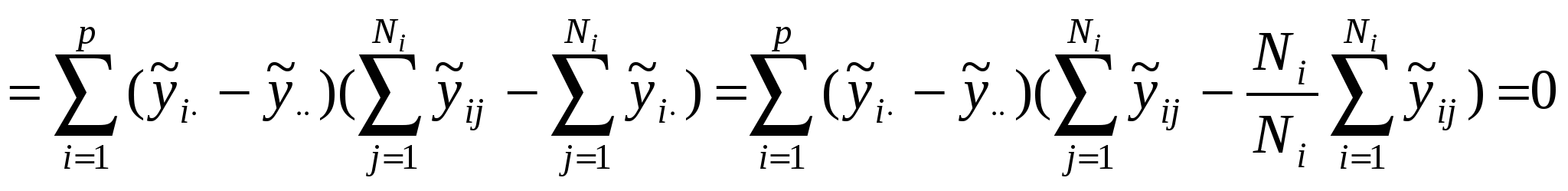 . .Соотношение (5.4) приобретает вид S0=Sму+Sву. Суммы S0 ,Sму ,Sву имеют N-1, p-1, N-p степеней свободы соответственно. Если имеет место проверяемая гипотеза Н0, то каждое из отношений: может служить оценкой дисперсии 2 случайных возмущений. В силу нормальности возмущений отношение Таблица 12
Гипотеза Н0: а1=а2=…=ар=0 отвергается при выбранном уровне надежности (обычно, 95%), если Fр>FТ, где FТ – табличное значение F-распределения при ЧСС числителя и знаменателя p-1 и N-pсоответственно. При FрFТ делается вывод, что результаты наблюдений не противоречат гипотезе Н0.
Исследуемая переменная у определяется теперь двумя факторами Aи В с p и q уровнями соответственно. На каждой из pq комбинаций уровней доступно по одному наблюдению. Для N=pq выборок единичного объема постулируется модель где m, ai, bj – параметры, uij – случайная компонента с теми же свойствами, что и в однофакторном ДА. Условий репараметризации здесь два: Применяя МНК, находят оценки параметров: 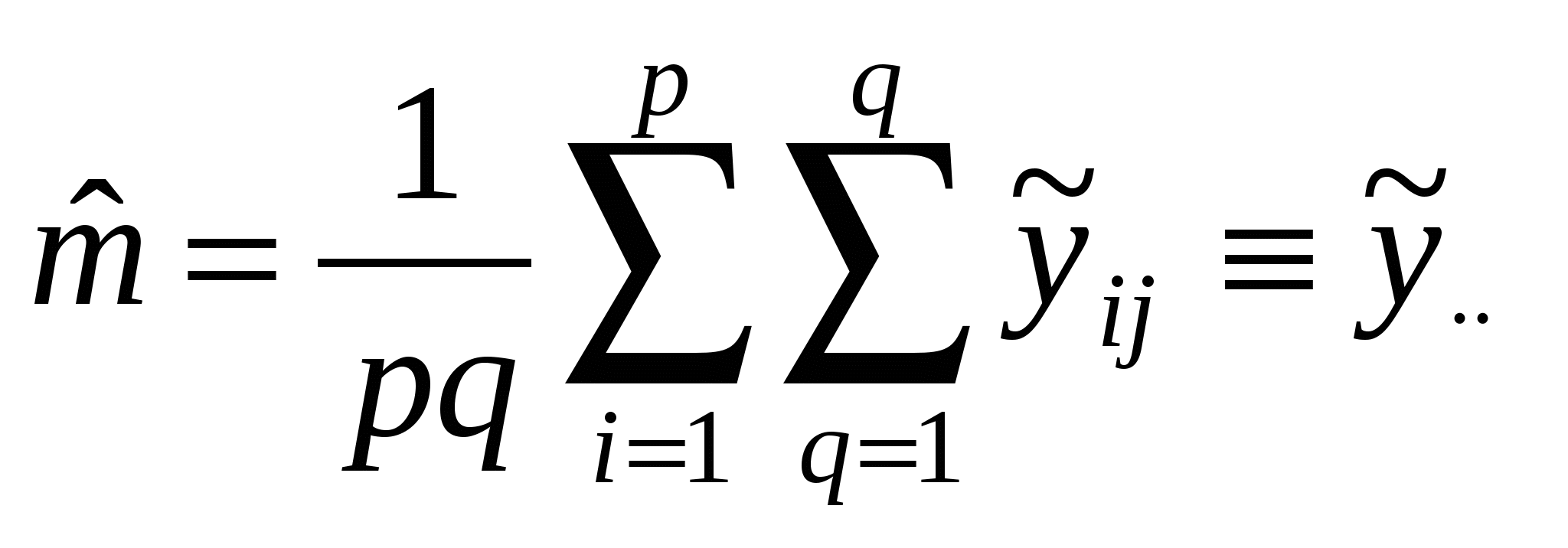 , , 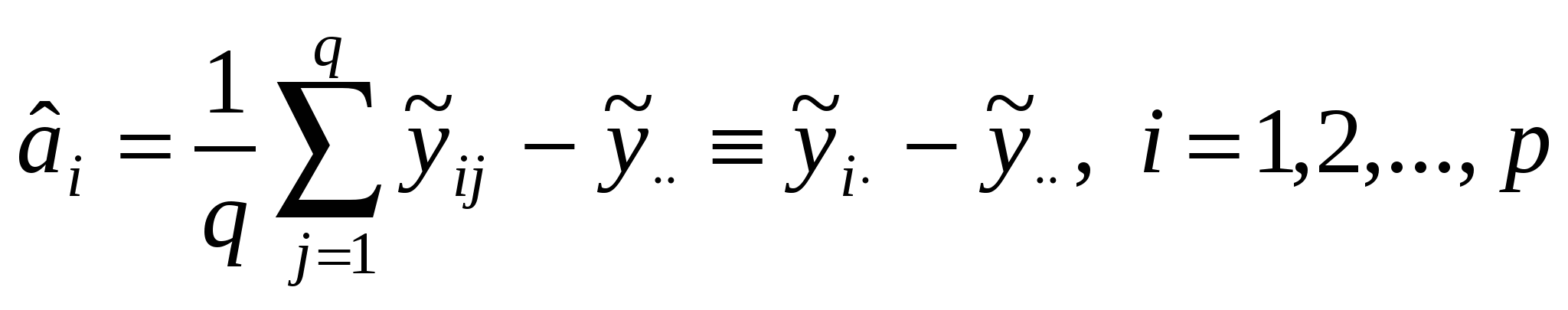 , ,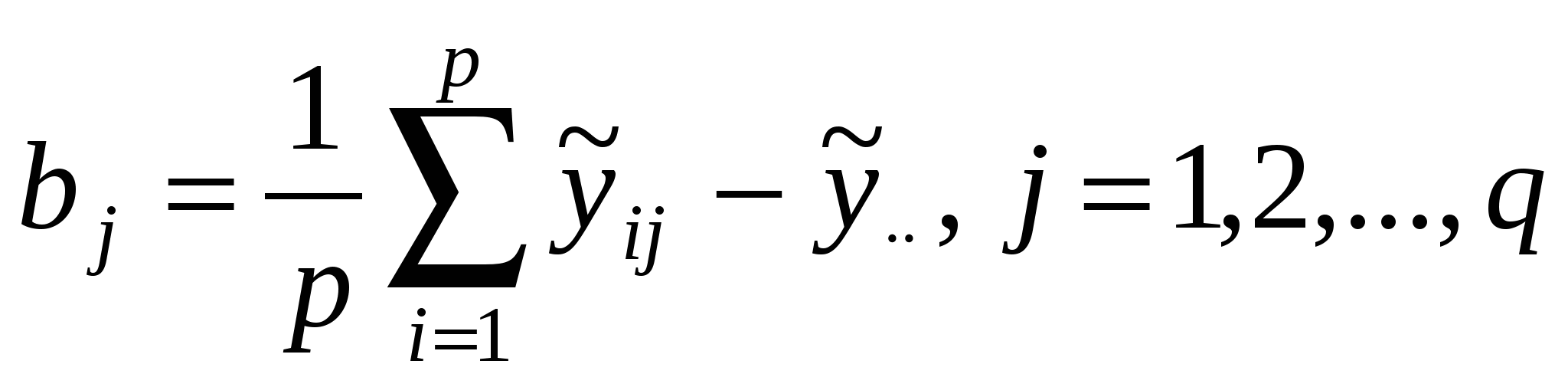 . .Основная задача двухфакторного ДА – проверка равенства нулю параметров ai и bj, т.е. проверка гипотез: НА: а1=а2=…=ар=0 и НВ: b1=b2=…=bq=0. Как и в однофакторном ДА, общую сумму квадратовS0 отклонений от общего среднего можно разложить на составляющие – теперь уже три: SA= 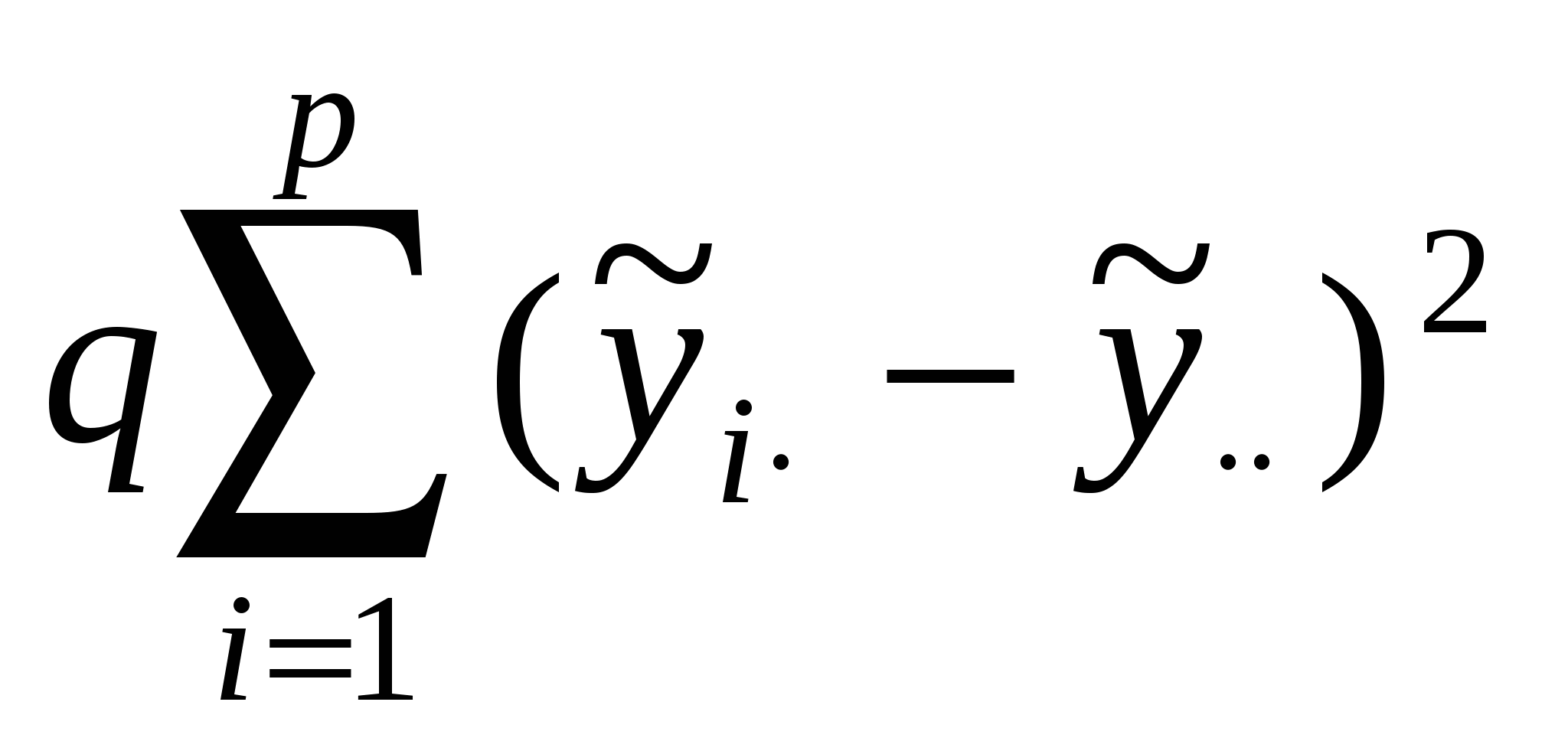 , SB= , SB=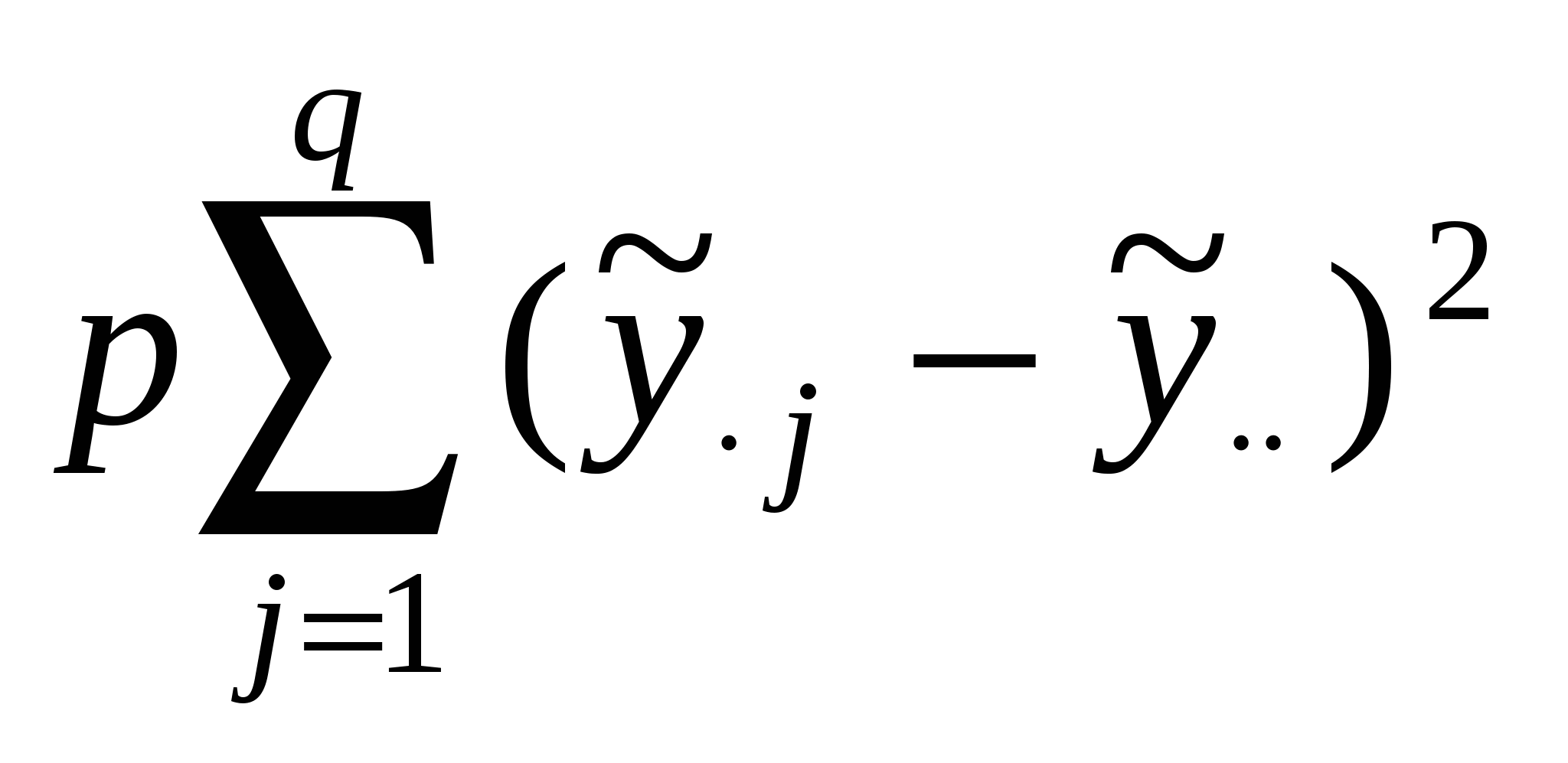 , обусловленные изменчивостью между уровнями факторов А и В соответственно, плюс слагаемое , обусловленные изменчивостью между уровнями факторов А и В соответственно, плюс слагаемое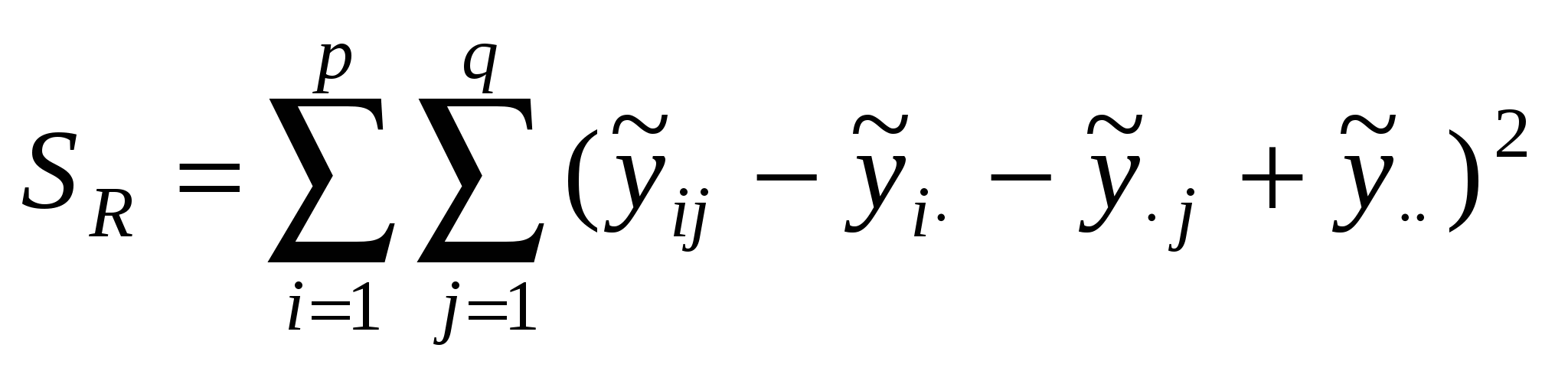 , связанное со случайной составляющей (экспериментальная ошибка). , связанное со случайной составляющей (экспериментальная ошибка).Схема вывода соотношения S0=SA+SB+SR (5.5) та же, что и в однофакторном ДА. За основу положено тождество: 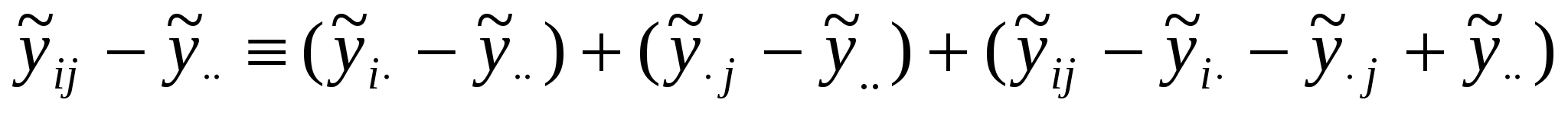 . .Исходные данные и результаты двухфакторного ДА принято представлять в виде табл.13 и 14. Таблица13
Таблица 14
Гипотеза НА (НВ) считается приемлемой, если FAFТА (FВFТВ), где FТА , FТВ – табличные значения F-распределения с ЧСС числителя и знаменателя в соответствии с табл.14.
Все многообразие критериев планирования эксперимента можно разбить на две большие группы Вторую группу составляют критерии, зародившиеся в практике планирования эксперимента и ориентированные на удобство расчетов и организации проведения экспериментов (критерии ортогональности и композиционности). Смысл перечисленных критериев можно пояснить, используя понятие эллипсоида рассеяния случайного вектора. Для случайного вектора а размерности описывающим эллипсоид в Критерий ортогональности Критерий ортогональности требует выбора плана Критерий композиционностиКритерий композиционности требует выбора плана, который включал бы в себя точки оптимального плана моделей более низкого порядка. Это обеспечивает сокращение числа опытов при поэтапном усложнении модели. На практике желательно использовать планы, удовлетворяющие одновременно нескольким критериям. В общем случае такого сочетания свойств не наблюдается. В теории планирования эксперимента доказано, что непрерывный D-оптимальный план является также G-оптимальным. Условие D-оптимальности дискретного плана Если для дискретного D-оптимального плана имеет место Построение D-оптимальных планов является сложной вычислительной задачей. Аналитический путь здесь оказывается возможным в некоторых простейших случаях (полиномиальная модель от одной переменной, квадратичная регрессия от | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
