Документ Microsoft Office Word (4). Размещение повторений. Повторения вопыте размещаются сплошным и разбросоным методом Размещение

• Название: Размещение повторений. Повторения вопыте размещаются сплошным и разбросоным методом Размещение
• Дата: 12.05.2019
• Размер: 0.93 Mb.
• Имя файла: Документ Microsoft Office Word (4).docx
• Тип: Документы; #76746
• страница: 1 из 4

Размещение повторений. Повторения вопыте размещаются сплошным и разбросоным методом

Размещение вариантов. Можно выделить три основные группы методов размещения вариантов по делянкам опытного участка: 1) стандартные, 2) систематические и 3) рендомизированные (случайные).

• 
  1. Стандартные методы основаны на том, что плодородие опытного участка изменяется постепенно, и между урожаями ближайших делянок наблюдается корреляционная связь. В стандартных методах каждый изучаемый вариант сравнивают со своим контролем, урожай которого вычисляют способом линейной интерполяции, находя промежуточные значения функции на основании предположения о постепенном изменении плодородия почвы земельного участка. К стандартным методам относятся: Ямб-метод, Дактель-метод.
  
• 
  2. Систематическое размещение вариантов — это такое расположение опыта, когда порядок следования вариантов в каждом повторении подчиняется определенной системе. Имеется много способов размещения вариантов по этому методу. В нашей стране распространены два — последовательный в один ярус и шахматный (или ступенчатый) при расположении повторений в несколько ярусов.
  

3. Подавляющее же большинство полевых опытов закладывают сейчас новыми методами, в основу которых положен принцип случайного, или рендомизировавного, размещения вариантов. Рендамизированные методы размещения вариантов: Метод неорганизованных повторений (полная рендамизация), Метод рендамизированных повторений, Латинский квадрат, Латинский прямоугольник, Метод расщипленных делянок, Метод решетки. Осуществление закладки и проведение опыта.
Результаты будут точными и надёжными если будут выдержаны все три этапа.

Основные элементы методики полевого опыта

Под МПО подразумевают совокупность слагающих элементов: число вариантов, площадь делянок, их форму и направление, схема опытов, повторность и повторение, методы размещения вариантов и повторений, защитные полосы, повторность опыта во времени, методы учёта урожая.

Число вариантов. Оно определяется целями и задачами опыта. Оптимальное количество вариантов от 4 до 12. Увеличение числа вариантов сверх этого на пёстрых по плодородию почвах, приводит к увеличению ошибки опыта. Если вариантов в опыте мало (2-3), то в этом случае увеличивается повторность, чтобы иметь достаточное число наблюдений для правильной оценки ошибки опыта.

По форме различают квадратную, прямоугольную и вытянутую делянки, при соотношении ширины и длины от 2 до 10. Наибольшее распространение получила прямоугольная форма. На практике ширина делянок определяется рабочим захватом обрабатывающих, посевных или уборочных агрегатов.

Оптимальным размеромплощади опытных делянок считают:

0,5 – 2 м² - в селекционной работе

10 – 15 м² - для газонов, цветочных и овощных культур (кроме бахчевых)

50 – 100 м² - для полевых культур сплошного сева

100 – 200 м² - для пропашных

Для производственных опытов площадь делянки может составлять от 100 до 3000 м² и более.

Оптимальное число учетных растений на делянке должно составлять 80 – 100 растений, для картофеля - 40 – 50, для кукурузы - 60 растений.

В условиях защищенного грунта размеры делянок составляют от 2-4 м² – для мелких овощей (редис, салат, петрушка, рассада, выгонка) до 8-15 м²– для крупных.

По назначению различают опытную и учётную площадь делянки. С учетной площади делянки учитывают урожай и проводят наблюдения, предусмотренные темой и программой исследования. Таким образом, опытная делянка включает в себя учётную площадь и защитные полосы.

В большинстве случаев ширину боковой защитной полосы, устанавливают в пределах 0,5 – 1,5 м, (в опытах с орошением и средствами защиты растение увеличивают до 2-3 и более метров. В опытах по сортоизучению, влиянием растений соседних делянок пренебрегают, и боковые защитные полосы не выделяют. Между делянками оставляют незасеянные полоски шириной 20-40 см.

Торцевые защитки шириной не менее 2 м выделяют для предохранения учётной части делянки от случайных повреждений.

Уборку урожая начинают с защитных полос и урожай обезличивают.

По всему периметру опытный участок окаймляет защитная полоса, шириной не менее 5 метров с посевом опытной культуры сплошного сева.

По направлению. Опытные делянки располагают в том направлении, в каком сильнее всего изменяется плодородие почвы.

Схема опытов – это совокупность (перечень) изучаемых в опыте вариантов

1. Посев 10 мая

2. Посев 15 мая Схема опыта считается основой опыта

3. Посев 20 мая

4. Посев 25 мая

К схеме опыта предъявляются следующие требования:

а) в ней обязательно выделяется контрольный вариант (стандарт)

б) схема опыта по возможности должна быть короткой (6-12 вариантов)

в) варианты должны быть контрастными, чтобы выявить различия в

урожайности

г) схема опыта должна быть составлена с учетом принципа единственного

различия. Варианты в опыте должны отличаться только по одному

признаку – изучаемому

Точность полевого эксперимента в большой степени определяется повторностью опыта на территории и во времени.

Повторность опыта на территории - это число, показывающее, сколько раз на территории опытного участка встречается делянка с одним и тем же вариантом (min – 3). Более точные результаты получаются при увеличении числа повторностей (opt – 6-8).

Повторность опыта во времени это число лет испытаний агротехнических приёмов или сортов.

Полевые опыты располагают методами организованных повторений и неорганизованных повторений (метод полной рендомизации).

Метод организованных повторений. Суть его заключается в том, что делянки с полным набором всех вариантов схемы объединяют территориально в компактную группу, составляя организованное повторение, которое занимает часть опытного поля

Организованное повторение - это часть площади опытного участка, включающая полный набор вариантов схемы опыта.

Применяют два способа размещения организованных повторений: сплошное, когда все повторения объединены территориально, и разбросанное,когда повторения по одному или по нескольку расположены в разных частях поля или даже на разных полях, в основном по причине неоднородности почвенного участка или по причине его маленького размера.

Метод неорганизованных повторений. При этом опыты могут размещаться на земельном участке без территориального объединения вариантов в компактные группы – повторения, а полностью случайно. Такое размещение называется полной рендомизацией. Оно используется только в тех редких случаях, когда нет необходимости ставить под контроль возможное закономерное варьирование условий эксперимента. (закладка небольшого опыта на хорошо выровненном земельном участке).

Методы размещения вариантов в опыте

 

Выделяют три группы методов размещения вариантов: стандартный, систематический и рендомизированный (случайный).

Стандартный метод применяется очень редко (в селекции), когда плодородие почвы характеризуется значительной пестротой. Данные, полученные в опыте, поставленного стандартным методом, можно обрабатывать наряду с дисперсионным, дробным и разностным методом. Варианты размещаются при этом методе в определённом порядке: контроль идёт или после каждого варианта (ямб-метод), или через два варианта (дактиль-метод)

Ямб-метод

к

к

Дактиль-метод

к

к

Стандартные методы постановки опытов имеют достоинство в том, что они позволяют более точно оценить изучаемые в опыте варианты (сорта), если плодородие опытного участка характеризуется значительной пестротой

Недостатки стандартного метода.

1. Нерационально используется площадь опытного участка, (более 50 % площади занято под контролем (стандартом).

2. Громоздкость постановки опыта

3. Увеличение объёмов всех выполняемых работ

Систематическое размещение вариантов это такое расположение опыта, когда порядок следования вариантов в каждом повторении подчиняется определенной системе.

Существует два способа размещения вариантов по этому методу:

а) последовательный в один ярус

б) шахматный - при размещении повторений в несколько ярусов.

 

 

Систематические методы применяются на выровненных по рельефу и плодородию участках. Математическую обработку данных можно провести дробным методом

Рендомизированный (случайный) метод размещения вариантов.

Используют три способа рендомизации.

1. С помощью карточек

2. С использованием специально разработанных схем

3. С использованием таблицы случайных чисел.

Рендомизированный метод был предложен английским учёным Фишером. Они позволяют дать более объективную оценку изучаемым вариантам и получить меньшую величину случайной ошибки.

Существует два способа рендомизации:

а) с использованием частичной рендомизации

б) полная (неограниченная) рендомизация

При частичной рендомизации опыты ставят методом организованных повторений. На опытном участке выделяют повторения, а внутри повторения варианты размещают рендомизированно. При этом опыт может быть поставлен: методом расщеплённых делянок или методом смешивания. Используют в опытах по сортоиспытанию, в которых изучаются много вариантов.

При полной рендомизации опыт ставят методом неорганизованных повторений. Опытный участок разбивают сразу разбивают на делянки и по ним размещают варианты рендомизированно. Применяется в отдельных случаях при закладке мелкоделяночных опытов с удобрениями, гербицидами. Такой опыт может быть поставлен методом латинского квадрата или прямоугольника.

Метод латинского квадрата используют при постановке опытов на небольших по размеру участках или плодородие на них изменяется в двух взаимно перпендикулярных направлениях

Требования при постановке опыта методом латинского квадрата

1. Опытный участок должен быть квадратной формы. Его разбивают на ряды и столбцы. Число их должно быть равным числу вариантов.

Ряды

С

Т

О

Л

Б

Ц

Ы

 

 

2. В каждом ряду и каждом столбце варианты размещаются рендомизировано.

3. Повторность опыта обязательно должна быть равна числу вариантов.(n =ℓ) ́Ν = ℓ² . Это ограничение является недостатком латинского квадрата. Поэтому латинский квадрат используют при количестве вариантов не менее 3 и не более 8 (ℓ = 3-8).

Недостаток латинского квадрата устраняется при методе латинского прямоугольника. Он не требует равенства повторности опыта числу вариантов, но обязательно число вариантов (ℓ) должно быть кратным повторности опыта (n). n : ℓ 4 : 12 = 3

 

15 вариантов ( 3×3×5)

I II III

Рекомендуют использовать при постановке опыта на участках, где плодородие почвы изменяется в двух взаимно перпендикулярных направлениях.

Данные опытов, поставленных с использованием рендомизированного размещения вариантов, обрабатывают методом дисперсионного анализа.

 

• 
  
  

Требования при постановке опыта методом латинского квадрата 1. Опытный участок должен быть квадратной формы. Его разбивают на ряды и столбцы. Число их должно быть равным числу вариантов.

2. В каждом ряду и каждом столбце варианты размещаются рендомизировано.

3. Повторность опыта обязательно должна быть равна числу вариантов.(n =ℓ) ́Ν = ℓ² . Это ограничение является недостатком латинского квадрата. Поэтому латинский квадрат используют при количестве вариантов не менее 3 и не более 8 (ℓ = 3-8).

Недостатки латинский квадрат:

1) число вариантов должно быть равно числу повторений.

2) С увеличением числа вариантов и соблюдением этого равенства, увеличивается количество опытных делянок, опыт становится громоздким при небольшой его информативности. Так, если в схеме опыта 10 вариантов, потребуется заложить 100 опытных делянок. Поэтому, считается нерациональным использование латинского квадрата при числе вариантов более 8. Отсюда, стремление найти другой метод размещения вариантов по принципу латинского квадрата, но без равенства n=l. Чтобы, не увеличивая повторности, использовать преимущество латинского квадрата, вариант опыта на опытных делянках необходимо размещать латинским прямоугольником.

 Латинский прямоугольник применяется, если число вариантов больше 8 и кратно числу повторностей. При числе вариантов 9 можно заложить опыт с трёхкратной повторностью, но нельзя при четырёхкратной. Если в схеме опыта 12 вариантов, размещение вариантов латинским прямоугольником возможно при 2, 3, 4 и 6 повторностях.

В основе латинского прямоугольника лежит латинский квадрат, форма которого определяется по числу повторностей. Чтобы квадрат преобразовать в прямоугольник, необходимо число вариантов разделить на число повторностей. На полученное число расщепить каждый ряд или столбец квадрата. Например, число вариантов в схеме опыта 12, повторность – четырёхкратная, число делянок – 48. Вначале строим латинский квадрат 4×4 (рис. 15 а). Затем каждый столбец расщепляем на 3 делянки (12:4 = 3). Получаем необходимое число делянок – 48. В каждом ряду и в каждом столбце будет 12 делянок, на которых размещаются варианты опыта. Так же, как и в латинском квадрате, столбцы и ряды содержат полный набор вариантов (рис.15 б).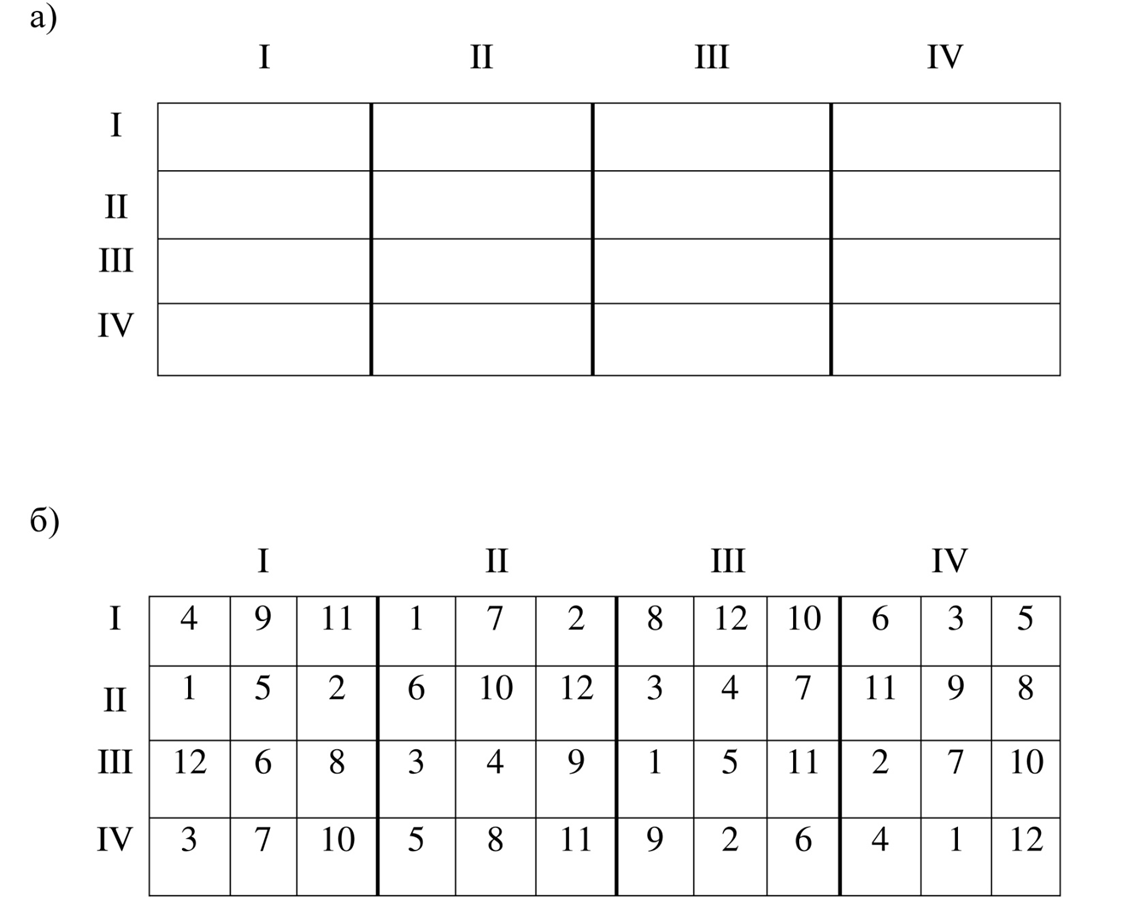



Рисунок 15 –Размещение вариантов латинским прямоугольником 4×4×3

 

Формула латинского прямоугольника записывается в виде произведения чисел. Например, 4×4×3, 5×5×3. Первые два множителя указывают, какой квадрат лежит в основе прямоугольника (4×4), (5×5), а третий – на сколько делянок необходимо расщепить каждый ряд, или столбец, чтобы превратить квадрат в прямоугольник. Произведение второго и третьего множителей указывает на число вариантов в схеме опыта. На рисунке 16 показаны схемы размещения опытов по методу латинского прямоугольника:



Рисунок 16 – Схемы размещения опытов с 15-20 вариантами методом латинского прямоугольника (Б.А. Доспехов, 1985)

 

Решетка применяется при большом числе вариантов – 25, 50 и более. Размещение полевого опыта методом организованных повторений позволяет контролировать варьирование урожайности и других наблюдений, вызванное различием плодородия между повторениями, но не учитывает территориальную неоднородность внутри их. При большом числе вариантов, когда увеличивается площадь, занятая отдельными повторениями, значительно ухудшается сравнимость вариантов.

Метод решетки, путем специального размещения вариантов, позволяет контролировать пестроту плодородия почвы не только повторения в целом, но и их отдельных его частей – блоков.

Существует много модификаций этого метода размещения вариантов.

Решетка может быть двухместная, трехместная, сбалансированная, прямоугольная и др. Наиболее простой и распространенной является простая двухместная решетка, которая характеризуется тем, что число вариантов в схеме опыта равно квадрату целого числа (16, 25, 36, 48 и т.д.). Варианты размещаются по блокам, а блоки объединяются в повторения. Число блоков в каждом повторении и число вариантов в блоке равно корню квадратному из числа вариантов 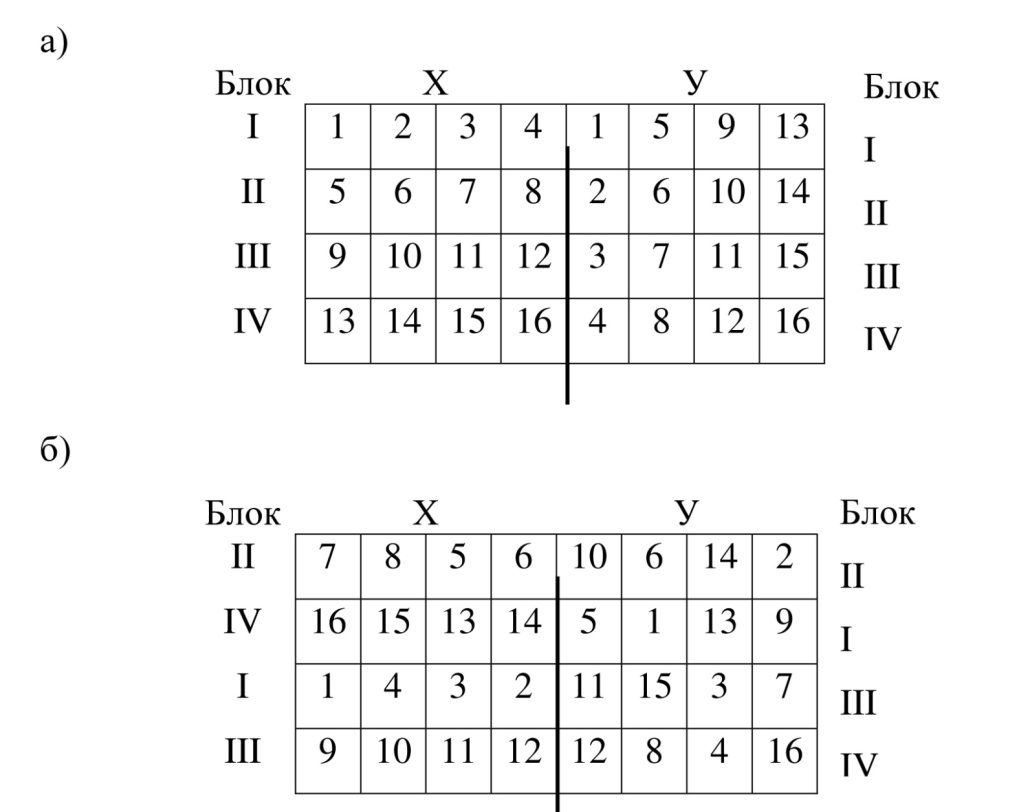 ) . Блоки в каждом повторении обозначаются римскими числами – I, II, III, IV и т.д. Простая двухместная решетка применяется при четном числе повторений. Нечетные повторения обозначаются «Х», четные – «Y». В повторении «Х» в блоках варианты размещаются по горизонтали, в повторении «Y» – по вертикали и так, чтобы варианты каждого блока повторения «Х», по одному входили во все блоки повторения «Y». На рисунке, а показано размещение по методу двухместной решетки 16 вариантов при двукратной повторности. Распределение блоков внутри повторения и вариантов внутри блока рекомендуется проводить случайно, т.е. рендомизировать (рис. 17аб).



Рисунок 17 – Размещение вариантов опыта по методу решетки

Расщепленная делянка. Все ранее рассмотренные методы размещения вариантов можно применять при проведении одно- и многофакторных опытов. Размещение вариантов по методу расщепленной делянки применяется только при закладке многофакторных опытов. При таком методе размещения варианты одного фактора (делянки первого порядка), используются для размещения вариантов второго фактора (делянки второго порядка), которые потом используются для размещения вариантов третьего фактора (делянки третьего порядка) и т.д. В агротехнических опытах на делянках первого порядка целесообразно изучать приемы, которые выполняются первыми (предшественник, обработка почвы). При проведении многолетних стационарных многофакторных опытов, методу расщепленных делянок следует отдавать предпочтение. В процессе опытной работы возникают новые идеи, мысли, требующие экспериментального изучения. Метод расщепленной делянки позволяет вводить для изучения новые факторы. Для введения новых вариантов расщепляют делянки предыдущих порядков.

Делянки первого порядка называют главными делянками, а делянки второго, третьего и т. д. порядков называют субделянками. По площади, главные делянки являются самыми крупными. По мере их расщепления, площадь делянок для последующих факторов уменьшается.

Варианты по главным делянкам и субделянкам размещают методом рендомизации. Особенность их размещения в том, что варианты главных делянок рендомизируются самостоятельно по каждому повторению, варианты второго и последующих порядков рендомизируются каждый раз заново. Размещение вариантов в трехфакторном опыте 3×2×3 по изучению предшественников (а0, а1, а2), обработок почвы (в0,в1) и удобрений (с0,с1,с2) по методу расщепленной делянки показано на рисунке 18.

 



Рисунок 18– Размещение вариантов опыта по методу расщепленной делянки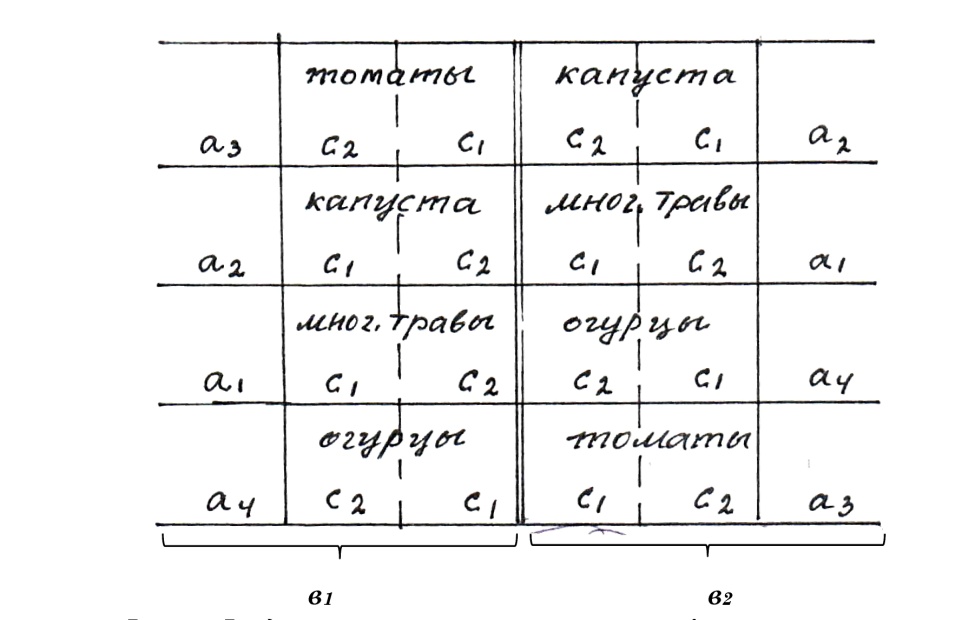



 

Рисунок 19 – Рендомезированное размещение трехфакторного опыта методом расщепленных делянок (в одном повторении):

а₁– многолетние травы; а₂ – капуста; томаты; а₃– огурцы

в₁ – одна норма орошения; в₂ – 1,5 нормы орошения

с₁ –одна норма удобрения; с₂–1,5 нормы удобрения

 Расщеплять опытные делянки можно в горизонтальном и вертикальном направлениях, что диктуется техническими условиями закладки и проведения полевого опыта. На рисунке 20 показано последовательное расщепление делянок в трехфакторном опыте.



Рисунок 20 – Схема последовательного расщепления вариантов в трехфакторном опыте с 24 вариантами (4×3×2)

Метод смешивания. В многофакторных опытах с увеличением числа факторов и вариантов по каждому фактору, увеличивается общее количество вариантов, для изучения которых требуется увеличение размера опытного участка. При этом из-за возможной неоднородности плодородия почвы варианты могут оказаться в неодинаковых условиях, нарушается принцип единственного различия, увеличивается ошибка, что неизбежно ведет к снижению точности исследования. Одним из эффективных приемов для снижения этих недостатков является применение при размещении вариантов метода смешивания.

Смешиванием называется такой метод размещения вариантов при котором в каждом повторении опыта варианты объединяются в группы (блоки), равноценные в отношении главных характеристик так, чтобы разности между группами составляли взаимодействие высшего порядка, представляющее меньший интерес, чем главные эффекты и взаимодействия между двумя факторами. В этом случае точность опыта определяется варьированием почвенного плодородия не по всему повторению, а внутри его части – внутри блока. Чтобы более точно сравнить варианты внутри блока, взаимодействия высшего порядка отождествляются, смешиваются с межблоковыми различиями, которые в условиях полевого опыта, как правило, не существенны и не представляют интереса.

На рисунке 21 показано размещение трехфакторного опыта по изучению удобрений: 0, N, Р, К, NР, NК, РК и NРК. Факторами здесь являются азотное, фосфорное и калийное удобрения, которые изучают в двух градациях (дозах) 0 и 1.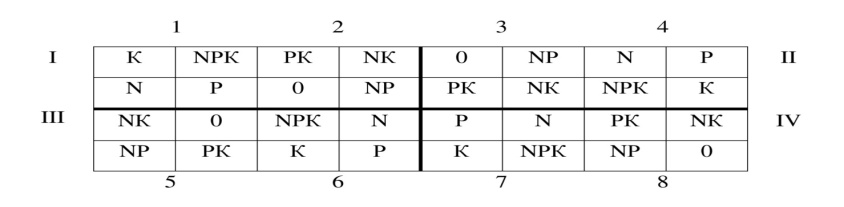



Рисунок 21 – Схема размещения трехфакторного опыта (2×2×2) методом смешивания в 8 блоках четырех повторений (смешано взаимодействие NРК)

Эффект тройного взаимодействия, которое жертвуется, определяется по формуле: (NРК) = ¼ (N+Р+К+NРК) – (0+NР+NК+РК). Если варианты N, Р, К, NРК расположить территориально в одном блоке, а варианты 0, NР, NК, РК – в другом, то тройное взаимодействие «смешивается» (отождествляется) с блоковыми различиями. Блокировка для опыта 2×2×2, в котором всего 8 вариантов, не является обязательной, но она становится необходимой, если число вариантов более 16-20 и территориальные размеры повторения становятся большими, что ведет к увеличению ошибки опыта.

 

Учёт урожая

Различают три метода учета урожая: сплошной, пробными площадками и снопами. В первом случае урожай с каждой учетной делянки убирают и взвешивают, а при втором методе учитывают урожай только с пробных делянок. При сноповом методе (травы, лён), учитывают биологический урожай (сырой), затем по пропорции рассчитывают товарную продукцию, семена, волокно, сено).

1. Сущность и схема дисперсионного анализа

Дисперсионный анализ основан на работах знаменитого математика Р.А.Фишера (30-е годы 20 в.). Несмотря на достаточно солидный «возраст», данный метод до сих пор остается одним из основных при проведении биологических и сельскохозяйственных исследований. Идеи, положенные в основу дисперсионного анализа, широко используются во многих других методах математического анализа экспериментальных данных, а также при планировании биологических и сельскохозяйственных экспериментов.

Дисперсионный анализ позволяет:

1) сравнивать две или несколько выборочных средних;

2) одновременно изучать действие нескольких независимых факторов, при этом можно определить как эффект каждого фактора в изменчивости изучаемого признака, так и их взаимодействие;

3) правильно планировать научный эксперимент.

Изменчивость живых организмов проявляется в виде разброса или рассеяния значений отдельных признаков в пределах, которые определяются степенью биологической выравненности материала и характером взаимосвязей с условиями среды. Признаки, изменяющиеся под воздействием тех или иных причин, называют результативными.

Факторы, влияющие на степень варьирования результативного признака, делятся на:

1)регулируемые

2) случайные

Регулируемые (систематические) факторы вызываются действием изучаемого в эксперименте фактора, который имеет в опыте несколько градаций. Градация фактора - это степень его воздействия на результативный признак. В соответствии с градациями признака выделяется несколько вариантов опыта для сравнения. Поскольку эти факторы предварительно обусловлены, их называют регулируемыми в исследованиях, т.е. заданными, зависящими от организации опыта. Следовательно, регулируемые факторы – факторы, действие которых изучается в опыте, именно они и обусловливают различия между средними выборочными разных вариантов - межгрупповую (факториальную) дисперсию.

Случайные факторы определяются естественным варьированием всех признаков биологических объектов в природе. Это неконтролируемые в опыте факторы. Они оказывают случайное влияние на результативный признак, обусловливают экспериментальные ошибки и определяют внутри каждого варианта разброс (рассеяние) признака. Этот разброс носит название внутригрупповой (случайной) дисперсии.

Таким образом, относительная роль отдельных факторов в общей изменчивости результативного признака характеризуется дисперсией и может быть изучена с помощью дисперсионного анализа или анализа рассеяния

Дисперсионный анализ основан на сравнении межгрупповой и внутригрупповой дисперсий. Если межгрупповая дисперсия не превышает внутригрупповую, значит, различия между группами имеют случайный характер. Если межгрупповая дисперсия существенно выше, чем внутригрупповая, то между изучаемыми группами (вариантами) существуют статистически значимые различия, обусловленные действием изучаемого в опыте фактора.

Из этого следует, что при статистическом изучении результативного признака при помощи дисперсионного анализа следует определить его варьирование по вариантам, повторениям, остаточное варьирование внутри этих групп и общее варьирование результативного признака в опыте. В соответствии с этим различают три вида дисперсий:

1) Общую дисперсию результативного признака (S_y²);

2) Межгрупповую, или частную, между выборками (S_y²);

3) Внутригрупповую, остаточную (S_z²).

Следовательно, дисперсионный анализ – это расчленение общей суммы квадратов отклонений и общего числа степеней свободы на части или компоненты, соответствующие структуре эксперимента, и оценка значимости действия и взаимодействия изучаемых факторов по F-критерию. В зависимости от числа одновременно исследуемых факторов различают двух-, трех-, четырехфакторный дисперсионный анализ.

При обработке полевых однофакторных статистических комплексов, состоящих из нескольких независимых вариантов, общая изменчивость результативного признака, измеряемая общей суммой квадратов (С_y), расчленяется на три компонента: варьирование между вариантами (выборками) - С_V, варьирование повторений (варианты связаны между собой общим контролируемым условием – наличием организованных повторений) - С_p и варьирование внутри вариантов С_z.. В общей форме изменчивость признака представлена следующим выражением:

С_y = С_V +С_p + С_z.

Общее число степеней свободы (N -1) также расчленяется на три части:

степени свободы для вариантов (l – 1);

степени свободы для повторений (n – 1);

случайного варьирования (n – 1)×(l – 1).

Суммы квадратов отклонений, по данным полевого опыта – статистического комплекса с вариантами – l и повторениями – n, находят следующим образом. Сначала с помощью исходной таблицы определяют суммы по повторениям - Σ P , вариантам - Σ V и общую сумму всех наблюдений - Σ X.

Затем вычисляют следующие показатели:

Общее число наблюдений N = l × n;

Корректирующий фактор (поправку) С_кор = (Σ X₁)² / N;

Общую сумму квадратов Cy = Σ X₁² – C_кор;

Сумму квадратов для повторений C_p = Σ P² / (l –C_кор);

Сумму квадратов для вариантов C_V = Σ V² / (n – 1);

Сумму квадратов для ошибки (остаток) C_Z = C_y - C_p - C_V .

Полученные суммы квадратов C_V и C_Z делят на соответствующие им степени свободы и получают два средних квадрата (дисперсии):

Вариантов S_v² = C_V/ l – 1;

Ошибки S_Z² = C_Z / (n – 1)×(l – 1).

Оценка существенности разностей между средними

Полученные средние квадраты используют в дисперсионном анализе для оценки значимости действия изучаемых факторов путем сравнения дисперсии вариантов (S_v²) с дисперсией ошибки (S_Z²) по критерию Фишера (F = S_Y² / S_Z²). За единицу сравнения принимают средний квадрат случайной дисперсии, который определяет случайную ошибку эксперимента.

Применение критерия Фишера позволяет установить наличие или отсутствие существенных различий между выборочными средними, но не указывает конкретных различий между средними.

Проверяемой H_o - гипотезой является предположение - все выборочные средние являются оценками одной генеральной средней и различия между ними несущественны. Если F_факт = S_Y² / S_Z² ≤ F_теор, то нулевая гипотеза не отвергается. Между выборочными средними нет существенных различий, и на этом проверка заканчивается. Нулевая гипотеза отвергается при F_факт = S_Y² / S_Z² ≥ F_теорЗначение F- критерия для принятого в исследовании уровня значимости находят в соответствующей таблице с учетом степеней свободы для дисперсии вариантов и случайной дисперсии. Обычно пользуются 5% -ным уровнем значимости, а при более строгом подходе 1% - ным и даже 0,1% -ным.

2. Оценка значимости разности между средними по наименьшей существенной разности

Наименьшей существенной разностью (НСР) – является своеобразной ценой деления, разрешающей способностью опыта при оценке разности выборочных средних. Критерий НСР = t_0,5 * S_dуказывает предельную ошибку для разности двух выборочных средних.

Если фактическая разность больше НСР_0,5 (d ≥ НСР_0,5), то она значима, существенна, при d ≤ НСР_0,5 – несущественна.

Для определения НСР необходимо по данным дисперсионного анализа вычислить обобщенную ошибку средней: Sx = √ S² / n и ошибку разности средних S_d = √ 2S² / n. Значения t - критерия для принятого уровня значимости и числа степеней свободы остаточной дисперсии берут из таблицы.

В многофакторном опыте изучается действие и взаимодействие нескольких факторов на изменчивость результативного признака, поэтому каждому фактору задают несколько градаций. Это позволяет изучать действие каждого из них при нескольких градациях других факторов.

Эффект взаимодействия факторов составляет ту часть общей изменчивости, которая вызвана различным действием одного фактора при разных градациях другого. В полевом опыте часто эффект от совместного применения изучаемых факторов может быть выше (синергизм) или ниже (антагонизм) суммы эффектов от раздельного применения каждого из них. В первом случае имеет место положительное, во втором – отрицательное взаимодействие факторов. Если же факторы не взаимодействуют, то эффект от совместного применения равен сумме эффектов от раздельного их применения (аддитивизм).

При дисперсионном анализе данных многофакторного опыта используют те же принципы и расчеты дисперсий, что и при однофакторном. Однако при этом усложняется математическая модель анализа.

При обработке данных двухфакторного опыта сумма квадратов расчленяется на следующие компоненты:

C_y = C_A+ C_B + C_AB + C_P + C_Z.

Соответственно с указанными компонентами расчленяется и общее число степеней свободы:

N -1 = (l_A-1) + (l_B – 1) + (l_A - 1)×(l_B -1) + (n – 1) + (l – 1)×(n – 1).

Вегетационные опыты представляют собой статистические комплексы, состоящие из нескольких независимых выборок (вариантов). Независимость сопоставляемых вариантов достигается регулярным перемещением сосудов на вагонетке. Следовательно, в вегетационных опытах обычно нет территориально организованных повторений. Поэтому в однофакторном вегетационном опыте общее варьирование результативного признака разлагается на два компонента – варьирование вариантов и случайное варьирование и общее число степеней свободы:

С_y = С_V + С_z, N – 1 = (l -1) + (N -l).