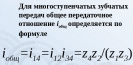ТММ вопросы. Вопросы. Разработкой общих методов исследования структуры, геометрии, кинематики и динамики типовых механизмов и их систем
 Скачать 2.52 Mb. Скачать 2.52 Mb.
|
|
Нормальное ускорение точки при движении относительно точки будет: Из точки (Рис.59,б) проводим линию, параллельную звену и откладываем отрезок : направив его от к . Из точки проводим перпендикуляр к до пересечения с линией Точку пересечения обозначим Снимем с плана ускорений значения  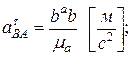 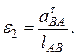 Определим направление по направлению ускорения Используя метод подобия 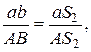 строим вектор строим вектор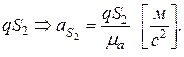 12. Последовательность построения плана скорости и плана ускорения для кулисного механизма? Дано: размеры звеньев, угловая скорость ведущего звена , положение ведущего звена . Определить: ускорения точек механизма А, С, D, угловые ускорения звеньев 3, 4.
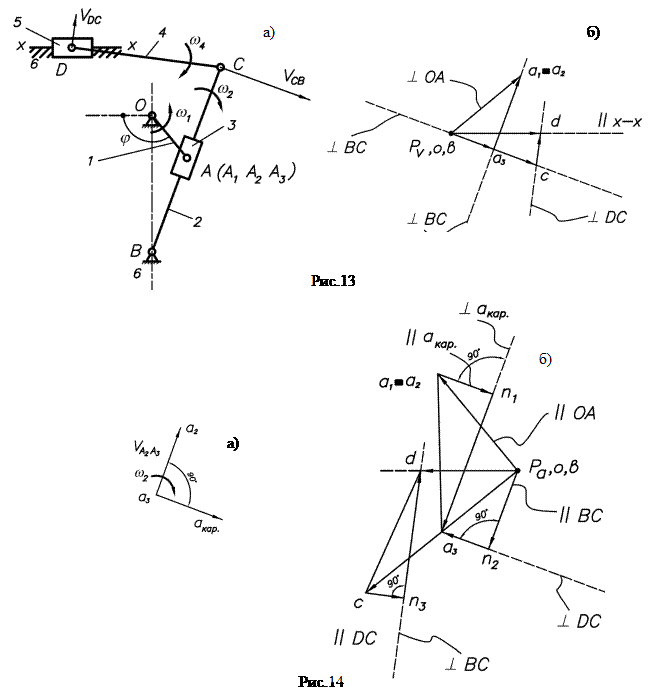
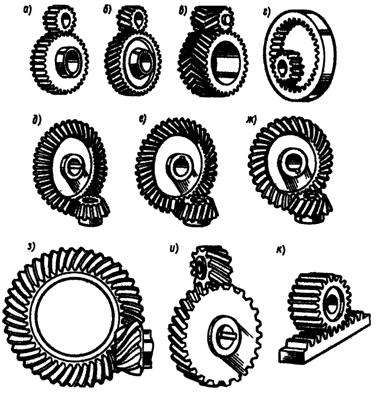
План механизма вычерчен в масштабе (рис.13а). Для механизма построен план скоростей (рис.13б). 1. Звено 1 вращается с постоянной угловой скоростью , поэтому: От полюса ра параллельно ОА в направлении от т.А к т.О (рис.14б) откладываем вектор , изображающий ускорение т.А1. 2. Как и при построении плана скоростей, движение т.А раскладываем на переносное (вращательное движение кулисы 3) и относительное (поступательное движение ползуна 2). Точка А1 тождественна точке А2 (А1 = А2), поэтому Движение шарнира А2 рассматриваем как сложное: вместе с кулисой 3 и относительно кулисы 3. На основании описанной выше процедуры сложного движения запишем:  где - вектор абсолютного ускорения точки А2, принадлежащей ползуну; Величина ускорения определяется как: Направлено параллельно АВ от т.А к т.В; вектор направлен . - вектор относительного ускорения т.А2 относительно т.А3 не известен по величине, но известен по направлению, параллелен АВ. - кориолисово ускорение т.А2: - определяется по плану скоростей. Направление определяется по правилу Жуковского (рис.14а) путем поворота вектора относительной скорости на 90° в направлении . Решаем графически уравнение таким образом, чтобы известный вектор был замыкающим в многоугольнике ускорений. Для этого от полюса р в направлении от А к В параллельно АВ откладываем вектор , через конец которого проводим линию действия . Вектор - замыкающий, поэтому к другому его концу (т. а2) пристраиваем известный вектор . Вектор можно пристраивать только так, как показано на плане ускорений (рис.14б). В противном случае вектор не будет замыкающим, т.е. результирующим векторной суммы. Через начало вектора (т.а2) параллельно АВ проводим линию действия относительного ускорения . В пересечении линий действия и получим точку а3 – решение данного уравнения. Согласно правилу векторной суммы расставим направление векторов, как показано на рис. 12б. Определяем значения ускорений: 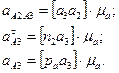 3. Определив ускорение т.А3 и зная, что в полюсе плана ускорений расположена точка в, соответствующая ускорению неподвижного шарнира В, из пропорции находим положение т.с на плане ускорений: Вектор представляет собой абсолютное ускорение т.С механизма: . 4. Для определения ускорения т. D составим уравнение: Абсолютное ускорение известно по направлению (// х–х), поэтому из полюса плана ускорений проводим прямую, параллельную х–х. К концу вектора параллельно DС в направлении от т.D к т.С пристраиваем вектор , величина которого Через конец вектора (т.d) проводим линию действия перпендикулярно DC. На пересечении этого перпендикуляра с горизонтальной прямой, проведенной через полюс ра, представляющей линию действия , получим т.d – конец вектора , выражающего ускорение т.D. Ускорения: 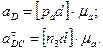 5. Величины и направления угловых ускорений звеньев определяем, как и в примере 1. - направлено против часовой стрелки. - направлено против часовой стрелки. 13. Кинематический анализ зубчатых передач. Какие виды зубчатых передач бывают? Для чего нужны зубчатые передачи? Определение передаточного отношения для простой зубчатой передачи? Внешнее и внутреннее зацепление. Определение передаточных чисел для рядовых (многоступенчатых) зубчатых передач. Представить пример многоступенчатой зубчатой передачи и рассчитать для него передаточное отношение. Зубчатая передача - трехзвенный механизм, включающий два подвижных звена, взаимодействующих между собой через высшую зубчатую кинематическую пару и образующих с третьим неподвижным звеном низшие (вращательные или поступательные) кинематические пары (рис. 4.1). Меньшее зубчатое колесо, участвующее в зацеплении обычно называют шестерней, большее – зубчатым колесом, звено зубчатой передачи, совершающее прямолинейное движение, называют зубчатой рейкой (рис. 4.1, к). Назначение зубчатой передачи - передача движения (чаще всего вращательного) с преобразованием параметров, а иногда и его вида (реечная передача). Зубчатые передачи вращательного движения наиболее распространены в технике (рис. 4.1, а…и). Они характеризуются передаваемыми мощностями от микроватт (механизм кварцевых наручных часов) до десятков тысяч киловатт (крупные шаровые мельницы, дробилки, обжиговые печи) при окружных скоростях до 150 м/с. Передаточное отношение зубчатой передачи – это отношение угловой скорости ведущего зубчатого колеса к угловой скорости ведомого зубчатого колеса. Ведущее зубчатое колесо – зубчатое колесо передачи, которое сообщает движение парному зубчатому колесу. Ведомое зубчатое колесо - зубчатое колесо передачи, которому сообщает движение парное зубчатое колесо. Передаточное отношение (иногда используется обозначение ) определяется при ведущем колесе 1, передаточное отношение определяется если ведущим является колесо 2:
 14. Что такое планетарная передача? Представить схему планетарной передачи, показать звенья планетарной передачи, как они называются, какие звенья являются подвижными, какие неподвижными? Чем планетарная передача отличается от дифференциальной? Формула Виллиса для определения передаточных чисел дифференциального механизма? Как определяются передаточные числа планетарных передач при различных неподвижных звеньях (представить примеры через угловые скорости и числа зубьев зубчатых колёс для 2 схем планетарных механизмов)? Планетарными называют передачи, имеющие зубчатые колеса с подвижными осями. Отличительной особенностью механизмов, включающих планетарную передачу (или передачи), является наличие двух или более степеней свободы. При этом угловая скорость любого звена передачи определяется угловыми скоростями остальных звеньев.  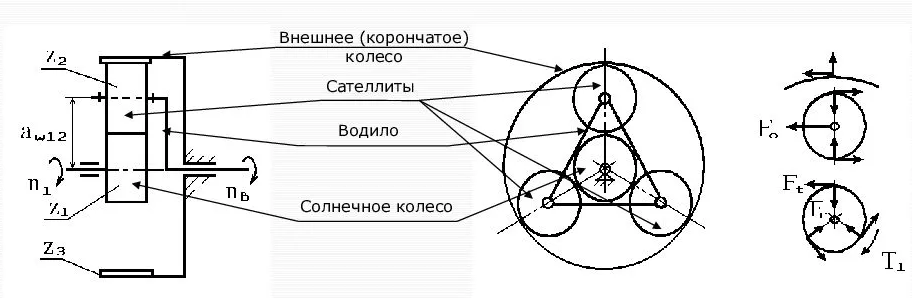 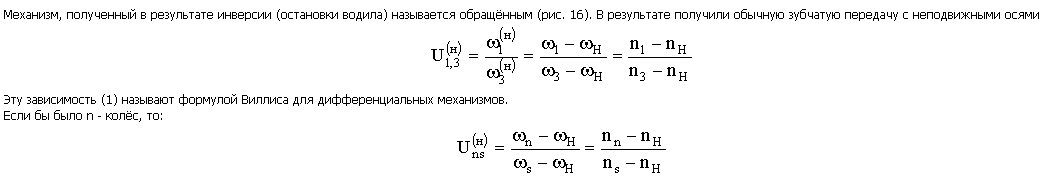 15. Основная теорема зацепления. Основная теорема зацепления Основная теорема зацепления (Виллиса) гласит: Общая нормаль в точке контакта сопряженных профилей в любой момент взаимодействия должна проходить через полюс зацепления, положение которого на межосевой линии делит ее на отрезки, обратно пропорциональные скоростям вращения колес, участвующих в зацеплении, т. е. |