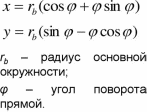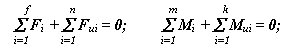ТММ вопросы. Вопросы. Разработкой общих методов исследования структуры, геометрии, кинематики и динамики типовых механизмов и их систем
 Скачать 2.52 Mb. Скачать 2.52 Mb.
|
|
где О1, О2 – центры вращения соответственно шестерни и зубчатого колеса, а О1О2 – межцентровое (межосевое) расстояние; Р – полюс зацепления (рис. 4.1). Профили зубьев, удовлетворяющие требованию основной теоремы зацепления, называются сопряженными. Таких профилей можно подобрать довольно много, но широкое распространение в машиностроении и приборостроении нашли предложенные Эйлером – эвольвенты. 16. Эвольвента окружности, уравнения эвольвенты, свойства эвольвенты. Эвольвентой окружности называется плоская кривая, которую описывает любая точка прямой линии, катящейся по окружности без скольжения. Эвольвента – это спиралеобразная кривая, имеющая две ветви с точкой заострения на основной окружности. Прямая, обкатывающаяся без скольжения по основной окружности, называется производящей прямой. Окружность, по которой катится прямая линия, образующая эвольвенту, называется основной окружностью (основа эвольвенты). Стандартное обозначение радиуса основной окружности - rb . Боковая поверхность зуба представляет собой звольвентную поверхность, которую образует траектория прямой линии находящейся на плоскости, катящейся по основному цилиндру без скольжения. Образование эвольвентной поверхности может быть представлено следующим образом. На барабан (основной цилиндр) намотана лента. Если с неподвижного барабана сматывать ленту, то конец ленты (и любая прямая на ленте ) будет описывать эвольвентную поверхность.
17. Свойства эвольвентного зацепления, что такое линия зацепления, угол зацепления, полюс зацепления, начальные окружности. 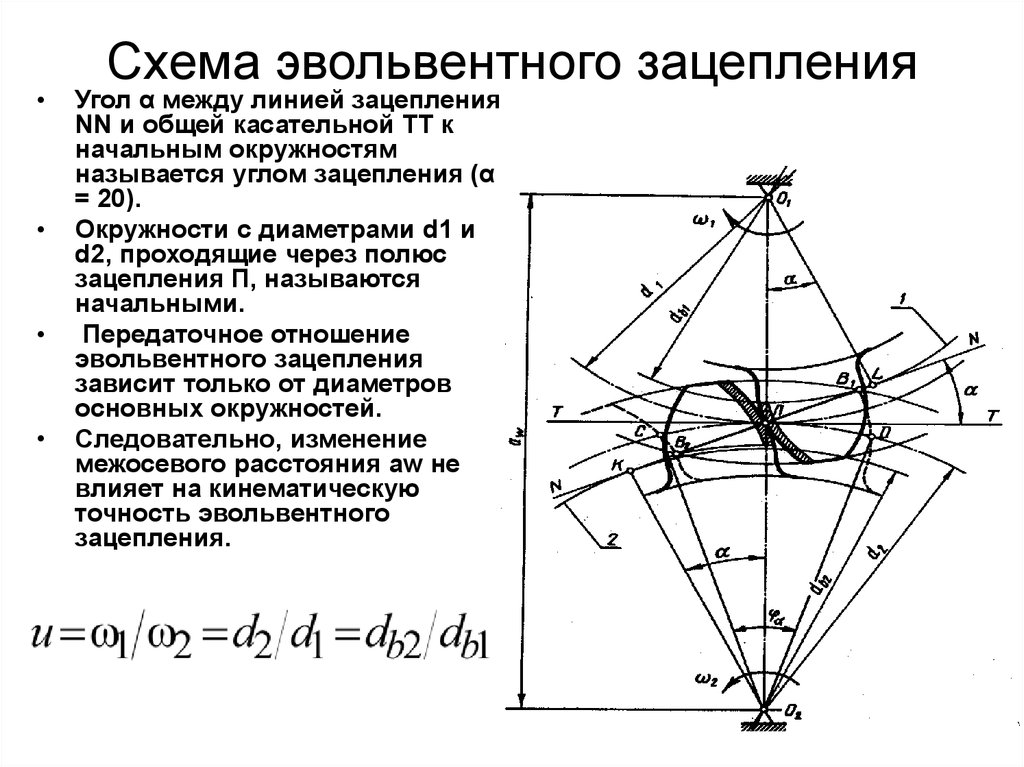 Линией зацепления называется геометрическое место точек соприкасания профилей боковых поверхностей зубьев колес, принадлежащее неподвижному пространству Полюс зацепления - мгновенный центр относительного вращения звеньев, образующих кинематическую пару. Начальная окружность- окружность, описанная около центра колеса и проходящая через полюс зацепления. 18. Основные размеры зубчатого колеса: радиус вершин, радиус впадин, модуль, делительная окружность, шаг зубьев, толщина зуба, ширина впадины.
Модуль − это число миллиметров диаметра делительной окружности зубчатого колеса, приходящееся на один зуб. Делительная окружность − это теоретическая окружность зубчатого колеса, на которой модуль и шаг принимают стандартные значения Делительная окружность делит зуб на головку и ножку. Начальная окружность – это теоретическая окружность зубчатого колеса, принадлежащая его начальной поверхности. Головка зуба – это часть зуба, расположенная между делительной ок-ружностью зубчатого колеса и его окружностью вершин. Ножка зуба – это часть зуба, расположенная между делительной окружностью зубчатого колеса и его окружностью впадин. Окружность вершин – это теоретическая окружность зубчатого колеса, соединяющая вершины его зубьев. Окружность впадин – это теоретическая окружность зубчатого колеса, соединяющая все его впадины. Окружной шаг, или шаг p − это расстояние по дуге делительной окружности между одноименными точками профилей соседних зубьев. Угловой шаг − это центральный угол, охватывающий дугу делительной окружности, соответствующий окружному шагу Шаг по основной окружности − это расстояние по дуге основной ок-ружности между одноименными точками профилей соседних зубьев Толщина зуба s по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей одного зуба Ширина впадины e по делительной окружности − это расстояние по дуге делительной окружности между разноименными точками профилей со-седних зубьев Толщина зуба Sb по основной окружности − это расстояние по дуге основной окружности между разноименными точками профилей одного зуба. Толщина зуба Sa по окружности вершин − это расстояние по дуге ок-ружности вершин между разноименными точками профилей одного зуба. Угол профиля α − это острый угол между касательной t – t к профилю зуба в точке, лежащей на делительной окружности зубчатого колеса и радиус-вектором, проведенным в данную точку из его геометрического центра 19. Зубчатая передача. Качественные показатели зубчатой передачи. Коэффициент перекрытия как определяется, что показывает. Как определить активную часть линии зацепления. Одним из качественных показателей зубчатой передачи является коэффициент перекрытия , равный Другим качественным показателем является коэффициент скольжения, который учитывает влияние геометрии передачи и её кинематики на скольжение и износ профилей, скользящих друг по другу (рис. 74), что видно из картины скоростей. На этой картине: - скорость точки к первого колеса; и Скорость скольжения колеса 1 и 2 относительно друг друга равна: Коэффициенты скольжения колёс 1 и 2 равны: 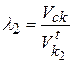 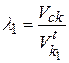 Эти коэффициенты равны нулю в полюсе (точка Р) и увеличиваются с удалением от него по линии зацепления. 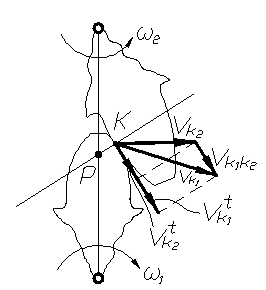 рис. 74 Таким образом, чем длиннее линия зацепления, (то есть, чем больше коэффициент перекрытия ), тем больше скольжение и износ профилей зубьев. линией зацепления зубчатой передачи является отрезок АВ, который представляет траекторию общей точки контакта двух сопряженных зубьев за период их зацепления Активной линией зацепления называется отрезок ab, представляющий собой часть линии зацепления АВ. Активная линия зацепления отсекается на прямой АВ окружностями вершин сопряженных зубьев. Длина активной линии зацепления обозначается буквой ga 20. Порядок силового анализа рычажного механизма. Основные задачи силового анализа. Определение сил инерции и моментов инерции. Реакции во вращательной и поступательной кинематических парах. Как направлены реакции? Реакция в высшей кинематической паре? Порядок (последовательность) силового анализа рычажного механизма: · Выделяем из механизма последнюю (крайнюю, наиболее удаленную от ведущего звена) структурную группу и проводим её силовой расчёт. Для этого: · прикладываем все внешние силы, действующие на звенья группы; · действие отсоединенных звеньев заменяем их реакциями; · прикладываем силы и моменты инерции; · определяем реакции, используя уравнения статики · Выделяем из механизма следующую структурную группу и проводим её силовой расчёт в таком же порядке. · Силовой расчёт заканчиваем силовым расчётом ведущего звена. Задачи: для исследуемого механизма при известных геометрических, кинематических и инерционных характеристиках и внешних силах: определить уравновешивающую силу или момент (управляющее силовое воздействие) и реакции в кинематических парах механизма. Кинетостатический расчет - для движущихся механизмов при известных массах и моментах инерции звеньев, когда пренебрежение инерционными силами приводит к существенным погрешностям; Уравнения кинетостатического равновесия:
где Fиi-инерционные силы, приложенные к звеньям, Mиi-моменты сил инерции, приложенные к звеньям. Сила инерции — сила, возникающая при разгоне или торможе -нии тела (материальной точки) и направленная в обратную сторону от ускорения. Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. 1. Реакция в поступательной кинематической паре V класса направлена перпендикулярно движению. Она известна по направлению, но неизвестны ее величина и точка приложения (рисунок 3.4, б). 2. Реакция во вращательной кинематической паре V класса проходит через центр шарнира, т.е. известна точка ее приложения. Величина и направление этой реакции неизвестны. Результирующая реакция R12 раскладывается на две составляющие: нормальная составляющая Rn12 направлена вдоль звена, а тангенциальная Rt12 – перпендикулярно звену (рисунок 3.4, а). 3. Реакция в высшей кинематической паре IV класса приложена к точке касания С звеньев 1 и 2 и направлена по общей нормали n-n (рисунок 3.4, в). Следовательно, известны направление и точка приложения этой реакции, а неизвестна ее величина. 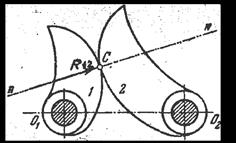 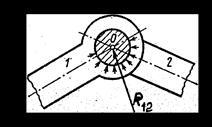 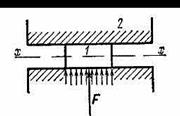 21. Порядок силового анализа группы Ассура. Рассказать последовательность выполнения силового анализа для двух любых групп Ассура. Что такое уравнение равновесия, какие уравнения равновесия используются в силовом анализе? Как определяется момент силы относительно точки? Что такое план сил, как его построить? Шаг 1: отсоединить группу Ассура от механизма и приложить к ней известные силы, в том числе и силы инерции, а действия звеньев заменить реакциями. Шаг 2: найти сумму моментов всех сил, действующих на одно звено группы Ассура, относительно точки (кинематической пары, так чтобы из полученного уравнения можно было найти значение тангенциальной составляющей реакции). Шаг 3: составить векторное уравнение всех сил, действующих на группу Ассура, которое равно нулю. В векторное уравнение войдут два неизвестных вектора, их пересечение при графическом построении даст нам решение векторного уравнения. 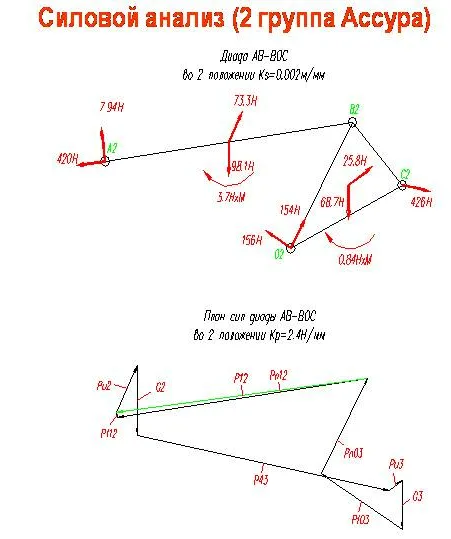 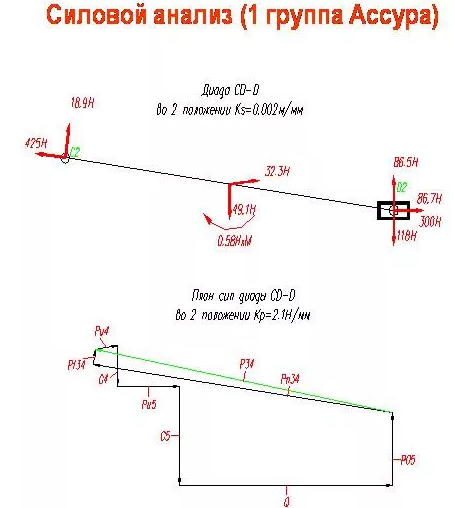 Уравнение равновесия описывает статическое или динамическое равновесие всех внутренних и внешних сил системы. 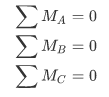 Момент силы относительно точки O - это векторная величина, определяемая векторным произведением радиус-вектора, проведенного из точки О к точке приложения силы, на вектор силы. Момент силы относительно точки O - это векторная величина, определяемая векторным произведением радиус-вектора, проведенного из точки О к точке приложения силы, на вектор силы. |