ТММ вопросы. Вопросы. Разработкой общих методов исследования структуры, геометрии, кинематики и динамики типовых механизмов и их систем
 Скачать 2.52 Mb.
|
|
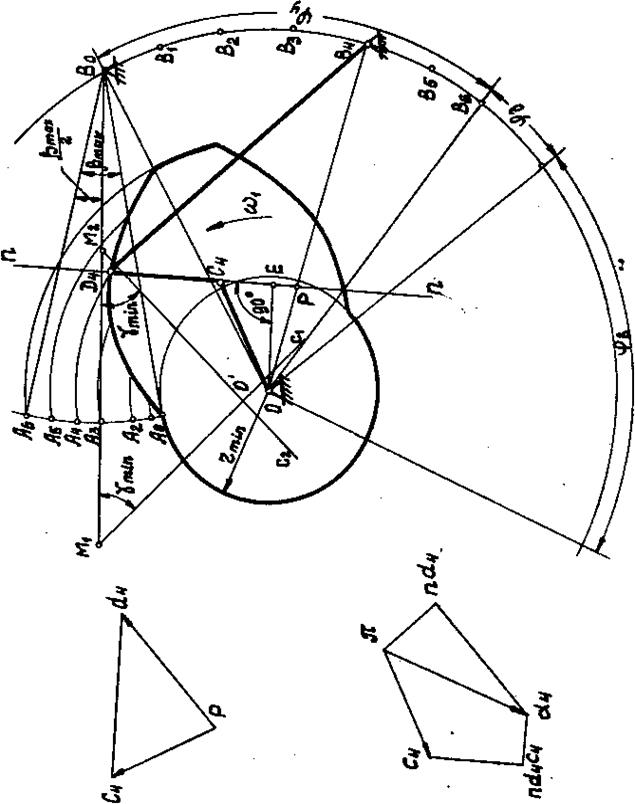
Планом сил называется замкнутый силовой многоугольник, построенный для каждой структурной группы и ведущего звена при данном положении механизма. План сил может быть построен при двух условиях: а) механизм находится в равновесии и б) механизм статически определим. 22. Из чего состоит кулачковый механизм. Приведите примеры кулачковых механизмов с различным движением кулачка и толкателя, с различными способами замыкания звеньев, с различными способами контакта кулачка и толкателя. Устройство кулачка – участки и фазовые углы. Законы движения толкателя – с жёстким ударом, с мягким ударом, безударные. Центровой профиль кулачка. Кулачковым называется трехзвенный механизм с высшей кинематической парой, входное звено которого называется кулачком, а выходное - толкателем (или коромыслом). Часто для замены в высшей паре трения скольжения трением качения и уменьшения износа, как кулачка, так и толкателя, в схему механизма включают дополнительное звено - ролик и вращательную кинематическую пару. Подвижность в этой кинематической паре не изменяет передаточных функций механизма и является местной подвижностью. Кулачковые механизмы предназначены для преобразования вращательного или поступательного движения кулачка в возвратно-вращательное или возвратно-поступательное движение толкателя. Большинство кулачковых механизмов относится к цикловым механизмам с периодом цикла равным 2p. В цикле движения толкателя в общем случае можно выделить четыре фазы: удаления, дальнего стояния (или выстоя), сближения и ближнего стояния. В соответствии с этим, углы поворота кулачка или фазовые углы делятся на: угол удаления jy угол дальнего выстоя jдв угол сближения jс угол ближнего выстоя jбв. Сумма трех углов образует угол jраб = dраб , который называется рабочим углом. jраб = dраб = jу + jдв + jс . Кулачок механизма характеризуется двумя профилями: центровым (или теоретическим) и конструктивным. Под конструктивным понимается наружный рабочий профиль кулачка. Теоретическим или центровым называется профиль, который в системе координат кулачка описывает центр ролика (или скругления рабочего профиля толкателя) при движении ролика по конструктивному профилю кулачка. Фазовым называется угол поворота кулачка. Профильным углом di называется угловая координата текущей рабочей точки теоретического профиля, соответствующая текущему фазовому углу ji. В общем случае фазовый угол не равен профильному ji¹di. Различают три группы законов движения, характеризующиеся следующими особенностями: 1. движение толкателя сопровождается жёсткими ударами, 2. движение толкателя сопровождается мягкими ударами, 3. движение толкателя происходит без ударов. Очень часто по условиям производства необходимо движение толкателя с постоянной скоростью. При применении такого закона движения толкателя в месте скачкообразного изменения скорости ускорение теоретически достигает бесконечности, бесконечно большими должны быть и динамические нагрузки. Практически вследствие упругости звеньев бесконечно большой динамической нагрузки не получается, но величина ее оказывается всё-таки очень большой. Такие удары называются "жесткими" и допустимы только в тихоходных механизмах и при малых весах толкателя. Мягкими ударами сопровождается работа кулачкового механизма, если функция скорости не имеет разрыва, но разрыв непрерывности претерпевает функция ускорения (или аналога ускорения) толкателя. Мгновенное изменение ускорения на конечную величину вызывает резкое изменение динамических усилий, которое также проявляется в виде удара. Однако эти удары менее опасны. Кулачковый механизм работает плавно, без ударов, если функции скорости и ускорения толкателя не претерпевают разрыва, изменяются плавно и при условии, что скорости и ускорения в начале и в конце движения равны нулю. 23. Сила давления кулачка на толкатель, угол давления и угол передачи движения в кулачковом механизме с поступательно-перемещающимся толкателем. На что влияют эти углы? Углом давления в кулачковых механизмах называют угол между общей нормалью к профилю кулачка в точке касания толкателя и направлением движения (скорости) толкателя Сила давления кулачка на толкатель F (без учета сил трения) направлена по нормали к профилю кулачка. Под действием движущей силы F cos толкатель поднимается и преодолевает силы полезных сопротивлений и силы трения в направляющих толкателя. Сила вызывает перекос толкателя и возникновение сил трения в направляющих толкателя. Если эта сила велика, то может произойти заклинивание и поломка толкателя. Для уменьшения силы выгодно, чтобы угол давления был как можно меньше. Однако, с другой стороны, с уменьшением угла возрастают размеры кулачка, что нежелательно Углом передачи движения (γ) называется нетупой угол между касательной к профилю кулачка, проведенной через точку контакта кулачка и толкателя, и вектором абсолютной скорости конца толкателя. Углом давления (α) в кулачковом механизме называется угол между нормалью к профилю кулачка (направлением силы нормального давления), проведенной через точку контакта кулачка и толкателя, и вектором абсолютной скорости конца толкателя. Для уменьшения составляющей силы нормального давления Р2 угол давления α целесообразно уменьшать. Углом передачи движения (γ) называется нетупой угол между касательной к профилю кулачка, проведенной через точку контакта кулачка и толкателя, и вектором абсолютной скорости конца толкателя. Угол передачи движения целесообразно увеличивать. 24. Как определить минимальный радиус кулачка аналитическим и графическим способами для механизмов с поступательно-перемещающимся толкателем и качающимся толкателем? На что влияет этот радиус? При проектировании кулачкового механизма очень важно правильно выбрать минимальный радиус кулачка rmin. Определение rminявляется одной из задач динамического синтеза кулачковых механизмов. Рассмотрим решение этой задачи применительно к конкретным схемам кулачковых механизмов. 1Нецентральный кулачковый механизм с поступательно движущимся толкателем (рис.7). Заданы: угол γmin , эксцентриситет е , ω1 и графики движения толкателя S=S (t), V=V (t). Величина угла передачи движения определяется по формуле 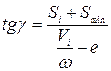 ,где Si – путь, пройденный толкателем при повороте кулачка из нулевого положения в данное, берется из графика S=S (t); Vi – скорость толкателя в рассматриваемом положении, берется из графика V=V (t); Smin – величина, определяющая крайнее (нижнее) положение толкателя. Задача динамического синтеза в данном случае сводится к определению такого значения Smin , при котором в любом положении угол передачи γ ≥ γmin . Если бы знали положение, в котором величина угла γ достигает наименьшего значения, то Smin можно было бы определить по формуле, вытекающей из формулы (9),  (9)Но так как мы не знаем, в каком именно положении угол γ получается наименьшим, то в этом случае приходится определять значения правой части неравенства (9) для несколько положений в пределах φу и наибольшее из них принимается равным Smin. После этого определяется rmin .  (10)Эту задачу можно решить графическим способом [4]. Следует также обращать внимание на расположение линии движения толкателя относительно цента вращения кулачка: при вращении кулачка против часовой стрелки выгоднее располагать ее справа от цента вращения О, так как в этом случае получаются большие значения угла передачи γ при удалении при одной и той же величине rmin , а следовательно, и более благоприятные динамические условия работы кулачкового механизма. 2Коромысловый кулачковый механизм (рис.8). Задан угол γmin , длина коромысла l ав , график движения толкателя S=S (t) и V=V (t) , ω1 . Угол передачи движения в этом случае определяется по формуле 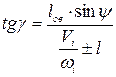 (11)где ψ – угол, составленный коромыслом в рассматриваемом положении с линей центров ОВ; Vi – скорость т.А коромысла, взятая с графика V=V (t); l – длина перпендикуляра, опущенного из т.О на направление скорости т.А; знак плюс или минус берется в зависимости от того, как расположен этот отрезок справа или слева от центра О. Задача динамического синтеза здесь сводится к определению начальных параметров кулачкового механизма: lОВ; rmin и угла ψо, который составляет коромысло в крайнем положении с линией центров ОВ. Проще всего эта задача решается графическим способом. При приближенном решении можно сделать допущение, что угол получается наименьшим как при удалении, так и при возвращении в тех положениях, где скорости толкателя имеет максимальное значение (обычно это середина фазы удаления и середина фазы возвращения). На основании этого производим следующее построение: а) изображаем толкатель в положении А3В0, соответствующем максимальному значению скорости т.А; б) откладываем вправо и влево, согласно правилу, приводимому ниже в примечаниях, отрезки  и  , где Vмах у и Vмахв – максимальное скорости т.А соответственно при удалении и и возвращении; в) из точек М1 и М2 под углом γmin к направлению коромысла проводим прямые М1С1 и М2С2, получаем точку пересечения их О1. Если теперь поместить центр вращения кулачка т.О внутри угла С1О'С2, то будет выполнено условие γ ≥ γmin во всех положениях; г) отложив угол А3В0А0, равный 0,5 βmax, получаем крайнее нижнее положение толкателя В0А0.Расстояние ОА0 будет равно rmin . Наименьшее значение получаем в том случае, когда центр вращения кулачка т.О помещаем в О'. ПРИМЕЧАНИЕ: I. Более точное решение этой задачи получим, если указанные построения проделаем для нескольких положений толкателя. Область, в которой можно поместить центр вращения кулачка О, получается в этом случае ограниченной сторонами построенных углов. II. Отрезок откладывается от т.А в направлении т.В, если кулачок и толкатель вращаются в одном направлении; при разном направлении вращений отрезок откладывается от т.А в обратном направлении.
|
