Развитие математической грамотности. Доклад «Развитие функциональной грамотности учащихся на уроках м. Развитие функциональной грамотности учащихся на уроках математики через практикоориентированные задания
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Задача 2. Показания счётчика электроэнергии 1 марта составляли 32767 киловатт-часов, а 1 апреля— 32965 киловатт-часов. По текущему тарифу стоимость 1 киловатт-часа электроэнергии составляет 3 рубля 40 копеек. Сколько нужно заплатить за электроэнергию за январь? Одна из распространённых ошибок при решении задачи про электроэнергию — просто умножить показания января на цену электроэнергии. Школьники получают при этом величину, превосходящую сто тысяч рублей, но не могут поймать себя на ошибке, так как не чувствуют величину этого числа. Важно привить школьникам умение анализировать полученный в задаче ответ с точки зрения здравого смысла. Задача 3. Установите соответствие между величинами и их возможными значениями. К каждому элементу первого столбца подберите соответствующий элемент из второго столбца.
Для её решения не нужно заучивать точные значения подобных величин. Достаточно привыкать к чувству порядка величины, изучая математику, физику, другие предметы. Задача 4. На рисунке изображены автобус и автомобиль. Длина автомобиля равна 4,2 м. Какова примерная длина автобуса? Ответ дайте в сантиметрах.  Часто это сбивает ребят, они не понимают, как решать такую задачу. Необходимо подчеркнуть, что в задаче просят оценить именно примерную длину, искать точное значение не требуется. Также важно обратить внимание школьников на единицы измерения, в которых необходимо дать ответ: длина автомобиля дана в метрах, а ответ нужно указать в сантиметрах. 2. Чтение текста Один из первых и самых ключевых навыков функциональной грамотности в математике — чтение сложных текстов, из которых не всегда очевидно, что именно требуется в задаче. К сожалению, этой теме уделяется мало внимания, особенно в старших классах. Статистика проведения ЕГЭ говорит о том, что даже в очень простых задачах школьники допускают обидные ошибки, неправильно читая условия задач и находя ответ не на тот вопрос, который предлагался в задаче. Например, в задаче на поиск меньшего корня квадратного уравнения школьники невнимательно читают условие и записывают в ответ значение большего корня. В 5-м и 6-м классах важно научить детей гибкому чтению на уроках математики. Важным признаком того, что условие прочитано неверно, может служить очень сложное решение или «некрасивый» ответ в задаче. Обсудим задачу-шутку, которая хорошо иллюстрирует, как важно внимательно читать условие. Задача 1. Представьте, что вы капитан авиалайнера, на котором путешествуют 300пассажиров. Этот самолет летит со скоростью 30 узлов в час (один узел равен 1,852 км/ч), предполагаемое время путешествия 18 часов. Сколько лет капитану корабля? Как правило, человек, решающий эту задачу, сразу переходит к анализу чисел и пропускает первую фразу. А именно она помогает ответить на вопрос задачи: решающему достаточно указать свой возраст. Рассмотрим ещё один пример задачи, требующей вдумчивого чтения условия. Задача 2. Братья Иван и Миша Ивановы играют в игру. Иван загадывает число n, имеющее ровно 7 простых делителей. Миша придумывает гладкое пятимерное многообразие, описываемое формулой степени не более чем n2. Иван указывает 5 точек на этом многообразии и объявляет длины не более чем 7 отрезков, соединяющих эти точки в пространстве R25. Если выбранные точки вместе с указанными Иваном отрезками образуют жёсткую структуру второго порядка, то побеждает Миша. В противном случае мальчики меняются местами: Иван придумывает другое гладкое многообразие, проходящее через эти 5 точек, и Миша указывает 5 точек на нём. Игра продолжается, пока либо у кого-то из мальчиков не получилась жёсткая структура, либо не прошло 1003 хода — в этом случае побеждает Миша. В зависимости от n назовите фамилию победителя при правильной игре. Задача отпугивает своим громоздким условием и сложными терминами, но на самом деле для решения задачи не требуется знаний топологии. Чтобы дать верный ответ на задачу, достаточно прочитать только первое и последнее предложения из условия. 3.Логическая грамотность Школьникам, которые никогда не будут использовать математику в работе, всё равно придётся принимать в жизни решения, которые будут основаны на анализе сложившейся ситуации, на анализе входных данных. Эти данные могут быть текстом договора, надписью на информационном щите, инструкцией к электроприбору и так далее. В этом блоке собраны примеры заданий, с помощью которых школьники смогут научиться отвечать на вопрос «следует ли из этой информации тот или иной вывод?». В ОГЭ, ЕГЭ есть задачи такого характера. Вот задача из открытых источников. Задача 1. Люди, проживающие в многоквартирном доме, решили выкупить этот дом. Они вместе хотят собрать деньги таким образом, чтобы каждый из них заплатил сумму, пропорциональную площади его квартиры. Например, мужчина, проживающий в квартире, которая занимает 1/5 площади всех квартир, должен будет заплатить 1/5 от всей стоимости здания. Выберите все верные утверждения. A. Человек, проживающий в самой большой квартире, заплатит больше денег за каждый квадратный метр своей квартиры, чем человек из самой маленькой квартиры. B. Зная площадь двух квартир и цену одной из них, мы можем вычислить цену второй. C. Зная цену здания и сумму, которую заплатит каждый владелец, мы можем вычислить общую площадь всех квартир. D. Если бы общая стоимость здания была снижена на 10%, каждый из владельцев заплатил бы на 10% меньше. В этой задаче верны утверждения B и D, а утверждения A и C неверны. Особенность следующей логической задачи заключается в том, что при её решении удобно использовать графическое представление. Задача 2. Кондитер испёк 40 печений, из них 10 штук он посыпал корицей, а 20 штук он собирается посыпать сахаром (кондитер может посыпать одно печенье и корицей, и сахаром, а может вообще ничем не посыпать). Выберите утверждения, которые будут верны при указанных условиях независимо от того, какие печенья кондитер посыплет сахаром.
A. Найдётся печений, которые ничем не посыпаны. B. Найдётся печений, посыпанных и сахаром, и корицей. C. Если печенье посыпано корицей, то оно посыпано и сахаром. D. Не может оказаться печений, посыпанных и сахаром, и корицей. 4. Незнакомый контекст Один из классических методических подходов к классификации сложности задач заключается в том, что решение задач базового уровня — это решение задач знакомыми методами в знакомой ситуации, задачи повышенной сложности — это решение задач знакомыми методами в изменённой ситуации, а задачи высокого уровня сложности требуют применения изученных методов в незнакомой ситуации. Задачи с незнакомым контекстом занимают значительное место в международных исследованиях качества образования, в том числе в исследовании PISA. В таких задачах описана незнакомая для человека ситуация, в которой ему необходимо применить зачастую совсем несложные математические методы. Такие задачи присутствуют и в ЕГЭ, и в экзамене за 9 класс, например, 10-я задача профильного экзамена. Чтобы решить задачу с незнакомым контекстом, необходимо внимательно прочитать условие, вычленить существенные части математической модели и значения тех или иных переменных и дать ответ, максимально абстрагировавшись от контекста. Задача 1. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 185 МГц. Скорость погружения батискафа v (в м/с) вычисляется по формуле v=c⋅(f−f0)/f+f0, где c=1500 м/c — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала (в МГц), регистрируемая приёмником. Определите частоту отражённого сигнала, если скорость погружения батискафа равна 20 м/с. Ответ дайте в МГц. Эту задачу можно упростить, если мысленно отбросить подробности сюжета и вычленить математическую модель. [...] испускает [...] импульсы частотой 185 МГц. Скорость погружения [...] v (в м/с) вычисляется по формуле v=c⋅(f−f0))/f+f0, где c=1500 м/c — скорость звука в воде, f0 — частота испускаемых импульсов (в МГц), f — частота отражённого от дна сигнала (в МГц), регистрируемая приёмником. Определите частоту отражённого сигнала, если скорость погружения батискафа равна 20 м/с. Ответ дайте в МГц. После такой процедуры становится понятно, что все значения переменных известны, кроме одного, и его уже несложно найти подстановкой в формулу. Задача 2. Автомобильное колесо, как правило, представляет из себя металлический диск с установленной на него резиновой шиной. Диаметр диска совпадает с диаметром внутреннего отверстия в шине. Для маркировки автомобильных шин применяется единая система обозначений. Например, 195/65R15 (рис. A). Первое число (число 195 в приведённом примере) обозначает ширину шины в миллиметрах (параметр B на рисунке Б). Второе число (число 65 в приведённом примере) — процентное отношение высоты боковины (параметр H на рисунке 2) к ширине шины, то есть 100⋅HB.  Последующая буква обозначает тип конструкции шины. В данном примере буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции. За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса d в дюймах (в одном дюйме 25,4 мм). Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, обозначающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие параметры. Завод производит легковые автомобили определённой модели и устанавливает на них колёса с шинами маркировки 165/70R13. 1. Завод допускает установку шин с другими маркировками. В таблице приведены разрешённые размеры шин.
1. На сколько миллиметров радиус колеса с шиной маркировки 205/55R14 больше, чем радиус колеса с шиной маркировки 165/65R14? Ответ округлите до десятых. 2. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить колёса, установленные на заводе, колёсами с шинами маркировки 175/60 R14? Результат округлите до десятых. 3. Дмитрий планирует заменить зимнюю резину на летнюю на своём автомобиле. Для каждого из четырёх колёс последовательно выполняются четыре операции: снятие колеса, замена шины, балансировка колеса и установка колеса. Он выбирает между автосервисами А и Б. Затраты на дорогу и стоимость операций приведены в таблице.
Сколько рублей Дмитрий заплатит за замену резины на своём автомобиле (включая дорогу), если выберет более дешёвый вариант? Работа с графическими представлениями информации Первый тип задач: Графики Информация, которую мы получаем, с течением времени представляется во всё более сложном виде, однако сам подход к чтению и осмыслению её не меняется — графическое представление информации бывает в виде графиков, диаграмм, схем и таблиц. Разберём задачу №2 из профильного ЕГЭ. Задача 1. На графике показано, как изменялась температура воздуха с 3 по 5 апреля. По горизонтали указано время суток, по вертикали — значение температуры в градусах Цельсия. 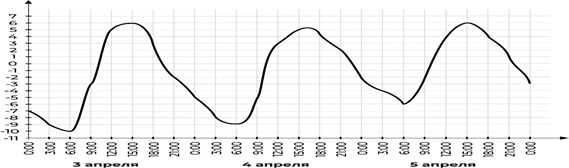 A. Найдите наименьшее значение температуры 4 апреля. Ответ дайте в градусах Цельсия. B. В течение скольких часов температура 5 апреля была меньше 4 градусов Цельсия? C. Найдите значение температуры 4 апреля в 3 часа дня. Ответ дайте в градусах Цельсия. Второй тип задач:Качественный анализ графиков Традиционно изучение графиков начинается с обсуждения практических графиков, например, графиков температуры или скорости. Но практически сразу акцент переносится на графики формальные, например, графики линейной или квадратичной функции. Типичным примером задачи на эту тему может быть следующая задача. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
