Развитие математической грамотности. Доклад «Развитие функциональной грамотности учащихся на уроках м. Развитие функциональной грамотности учащихся на уроках математики через практикоориентированные задания
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
Задача 2. Установите соответствие между графиками функций и характеристиками этих функций на отрезке [−1;1]. 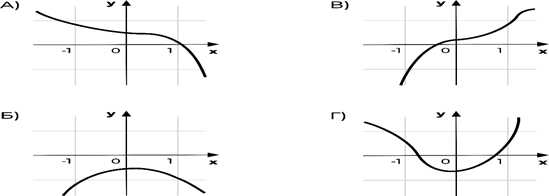 Характеристики. Функция имеет точку максимума на отрезке [−1;1]. Функция имеет точку минимума на отрезке [−1;1]. Функция возрастает на отрезке [−1;1]. Функция убывает на отрезке [−1;1]. В последнее время к таким задачам стали добавляться задачи на анализ практических графиков, например, следующая. Задача 3. На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя; на вертикальной оси — температура двигателя в градусах Цельсия. 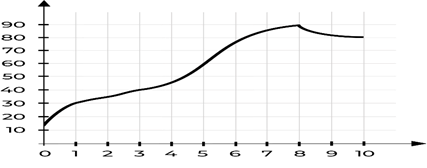 Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику процесса разогрева двигателя на этом интервале.
Ещё один пример практиориентированной задачи из материалов исследования PISA. Как правило это задачи с не очень чётким условием, при их решении нужно применять и математических знания, и умение внимательно читать условие, и здравый смысл. 6. Экономика — одно из наиболее естественных приложений математики и, наоборот, один из «заказчиков» создания математики. С такими задачами сталкивается любой ученик в реальной жизни, а как следствие — ещё и на экзаменах. Трудности, которые вызывают у многих учащихся даже несложные задачи на проценты, обычно во многом обусловлены достаточно формальным подходом к изложению темы. А ведь для решения подавляющего большинства задач на проценты достаточно понимать, что процент — это просто одна сотая часть числа. Поэтому для успешного решения задач на проценты достаточно научиться «переводить» условие задачи на язык десятичных дробей, а после её решения — делать обратный «перевод». На примере следующих пяти задач проделаем эти «переводы». Задача 1. Полотенце стоило 80 рублей. Ближе к дачному сезону оно подорожало на 25%. Сколько оно стало стоить? Задача 2. Полотенце стоило 100 рублей, но в конце сезона оно подешевело на 20%. Сколько стало стоить полотенце со скидкой? Задача 3. Розничная цена на полотенце составляет 100 рублей, при этом известно, что розничная цена образуется при наценке на оптовую цену 25%. Какова оптовая цена этого полотенца? Задача 4. Оптовая цена на полотенце составляет 80% от розничной. Какова розничная цена, если оптовая цена 80 рублей? Задача 5. В городе два магазина. В первом висит объявление о снижении цен на 80%, во втором — о снижении цен в 5 раз. В какой магазин пойти покупателю, если цены в обоих магазинах до снижения были одинаковыми? Проводились исследования, согласно результатам которых большинство людей выберет второй магазин, хотя цены в обоих окажутся одинаковыми. Важно уметь анализировать такие вещи и не попадаться на маркетинговые ходы. Ещё одним важным примером применения процентов является вычисление подоходного налога. Если в трудовом договоре работника написана некоторая сумма, например, 10000 рублей, то реально работник получит на руки эту сумму за вычетом подоходного налога 13%, т. е. 8700 рублей. При этом работодатель должен иметь около 13000 рублей, чтобы выплатить эту зарплату, так как он обязан отчислять около 30% от суммы, написанной в договоре, в фонды. Данные в экономических задачах часто приведены в виде таблиц. В таком виде они приходят к нам из коммерческих предложений, прайс-листов, рекламы, и в таком же виде они попали в базовый ЕГЭ. Ниже приведён пример простейшей задачи на прямое считывание из таблицы. Задача 6. В таблице представлены данные о стоимости некоторой модели смартфона в различных магазинах.
Найдите наименьшую стоимость смартфона среди представленных предложений. Ответ дайте в рублях. Задача 7. Интернет-провайдер (компания, оказывающая услуги по подключению к сети Интернет) предлагает три тарифных плана.
Пользователь предполагает, что его трафик составит 650 МБ в месяц, и исходя из этого выбирает наиболее дешёвый тарифный план. Сколько рублей заплатит пользователь за месяц, если его трафик действительно будет равен 650 МБ? Одна из проблем при решении такой задачи — желание решать её по аналогии с предыдущей задачей, прямым считыванием с графика. В данном случае такой метод решения уже не подходит, нужно аккуратно анализировать каждую строку таблицы. Стоит упомянуть, что в рекламных материалах и коммерческих предложениях некоторых компаний часто встречаются дополнительные условия, которые находятся в сноске под «звёздочкой». Научить ребят читать внимательно предложенную им информацию и не попадаться в ловушку — одна из наших задач. 7. Геометрия Функциональная грамотность в геометрии — один из важнейших блоков. Сама наука геометрия произошла благодаря запросам повседневной жизни к науке. Геометрия окружает нас повсюду, например, в архитектуре и картах. Иногда она появляется там, где мы её совсем не ждём — в еде, например, (мы разберём в разделе несколько задач про это). Поэтому важно развивать геометрическую интуицию и уметь применять геометрические методы на практике. Одна из ролей, которую играет геометрия в школе, — развитие логики. Большое внимание в школьном курсе геометрии уделяется доказательствам геометрических утверждений, в задачах по планиметрии и стереометрии используется много формул и вычислений. Необходимо развивать геометрическую интуицию, решать задачи с практическим содержанием. Часто школьники ещё не готовы к такой подаче материала, поэтому важно с начальной школы познакомить ребят с большим количеством несложных наглядных геометрических сюжетов. В качестве примера практической геометрической задачи обсудим постановку задачи на план местности. Очень важно научить детей по длинному заданию текста решать такие задачи, с карандашом в рука аккуратно, шаг за шагом. Задача 1. Таня на летних каникулах приезжает в гости к дедушке в деревню Антоновка (на плане обозначена цифрой 1). В конце каникул дедушка на машине собирается отвезти Таню на автобусную станцию, которая находится в деревне Богданово. Из Антоновки в Богданово можно проехать по просёлочной дороге мимо реки. Есть другой путь — по шоссе до деревни Ванютино, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Богданово. Третий маршрут проходит по просёлочной дороге мимо пруда до деревни Горюново, где можно свернуть на шоссе до Богданово. Четвёртый маршрут пролегает по шоссе до деревни Доломино, от Доломино до Горюново по просёлочной дороге мимо конюшни и от Горюново до Богданово по шоссе. Ещё один маршрут проходит по шоссе до деревни Егорка, по просёлочной дороге мимо конюшни от Егорки до Жилино и по шоссе от Жилино до Богданова. Шоссе и просёлочные дороги образуют прямоугольные треугольники. 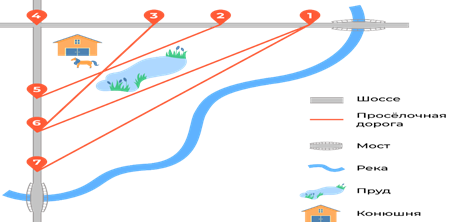 Расстояние от Антоновки до Доломино равно 12 км, от Доломино до Егорки — 4 км, от Егорки до Ванютино — 12 км, от Горюново до Ванютино — 15 км, от Ванютино до Жилино — 9 км, а от Жилино до Богданово — 12 км. А) Пользуясь описанием выше, определите, какими цифрами на плане обозначены деревни Ванютино, Горюново, Егорка, Жилино. В поле ввода ответов введите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов в том порядке, в котором перечислены соответствующие им деревни. Б) Сколько минут затратят на дорогу Таня с дедушкой из Антоновки в Богданово, если поедут мимо пруда через Горюново? В) Найдите расстояние от Антоновки до Егорки по шоссе. Геометрия. Масштаб Одним из важных геометрических понятий является понятие масштаба, которое теряется в школьном курсе. Реально масштаб изучается только на уроках географии, а развитию интуитивного понимания масштаба на уроках математики времени уделяется мало. Задача 2. Грузчик на складе может поднять упаковку размером 3×3×3 литровых пакетов молока. Смогут ли три грузчика поднять упаковку 9×9×9 пакетов? Даже если просто подсчитать вес большой упаковки: 9×9×9=729 пакетов, то есть примерно 729 кг, станет ясно, что втроём её не поднять. В любом случае, стоит разобраться, из скольких же маленьких упаковок состоит большая. Задача. 4 В сосуд, имеющий форму конуса, налили 25 мл жидкости до половины высоты сосуда (см. рисунок). Сколько миллилитров жидкости нужно долить в сосуд, чтобы заполнить его доверху? 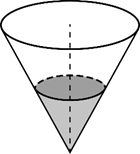 8. Урезанное среднее Различные средние величины Начнём обсуждение средних величин с конкретного примера про среднюю скорость. Задача 1. Автомобиль двигался первую половину времени, проведённого в пути, со средней скоростью v1=40 км/ч, а вторую половину времени — со средней скоростью v2=80 км/ч. В этом случае средняя скорость на всём пути составляет (40+80):2=60 км/ч. Здесь мы вычислили среднее арифметическое двух скоростей. На практике такая ситуация довольно плохо реализуема, задача получается искусственной. Вспомним две средние величины: среднее арифметическое и медиану, и обсудим задачу из этого раздела. Задача 2. Средний рост учащихся в классе 165 см. Медиана роста равна 168 см. Укажите верные утверждения. 1. В этом классе не меньше половины учеников выше 165 см. 2. В этом классе не меньше половины учеников выше 168 см. 3. В этом классе обязательно найдётся ученик, рост которого больше 165, но меньше 168 см. 4. В этом классе обязательно найдётся ученик ростом ровно 168 см. 5. В этом классе обязательно найдётся ученик, рост которого меньше 165 см. Таким образом, подводя итог, можно сказать, что Для решения проблемы математически грамотный учащийся сначала должен увидеть математическую природу проблемы, представленной в контексте реального мира, и сформулировать ее на языке математики. Это преобразование требует математических рассуждений и, возможно, является центральным компонентом того, что значит быть математически грамотным. Это один из навыков XXI века. В настоящее время школа пока ещё продолжает ориентироваться на обучение, выпуская в жизнь человека обученного, но тогда как сегодняшнее, информационное общество запрашивает человека обучающегося, способного самостоятельно учиться и готового к реальным действиям и принятию решений. Это определяет значимость математики в формировании у учащихся умений решать задачи, возникающие в процессе практическойдеятельности человека. В этом и заключается актуальность рассматриваемой темы. Список литературы: 1. оf. fipi.ru Федеральный институт педагогических измерений. Банк открытых заданий. 2. hpps://oge.sdamgia.ru/Образовательный портал 3. СДАМ ГИА: РЕШУ ВПР, ОГЭ, ЕГЭ и ЦТ.Образовательный портал для подготовки к экзаменам 4. ОГЭ-2020. Математика. 9 класс. Основной государственный экзамен. /И.Р. Высоцкий, Л.О. Рослова, Л.В. Семенов, П. И. Захаров; под ред. И.В. Ященко.- М.: Издательство «Экзамен»,МЦНМО,2020.) 5. С.С. Минаева. Дроби и проценты.5-7 классы. ФГОС/.-М.: Издательство «Экзамен», 2016.- 125 с. 6. Калинкина Е.Н. Сборник заданий по развитию функциональной математической грамотности обучающихся 5-9 классов. -Новокуйбышевск, 2019. 7. Козлова С.А. Контрольно-измерительные материалы. Тесты и самостоятельные работы к учебнику «Математика», 5 кл. /С.А.Козлова, А.Г. Рубин, В.Н. Гераськин.-М.: Баласс, 2014.-112с. 8. Развитие функциональной грамотности обучающихся основной школы: методическое пособие для педагогов /Под общей редакцией Л.Ю. Панариной, И.В. Сорокиной, О.А. Смагиной, Е.А. Зайцевой. – Самара: СИПКРО, 2019. - с. 9. Сергеева Т.Ф. Математика на каждый день.6-8 классы: пособие для общеобразовательных организ./Т.Ф. Сергеева.- М.: Просвещение, 2020.-112 с. |
