Развитие математической грамотности. Доклад «Развитие функциональной грамотности учащихся на уроках м. Развитие функциональной грамотности учащихся на уроках математики через практикоориентированные задания
 Скачать 0.56 Mb. Скачать 0.56 Mb.
|
|
МАСТЕР-КЛАСС ПО ТЕМЕ: «Развитие функциональной грамотности учащихся на уроках математики через практико-ориентированные задания» Подготовила: учитель математики МБОУ СОШ №2 г.о. Реутов Кузьмина Наталья Александровна 2021-2022 учебный год Функциональная грамотность – умение решать жизненные задачи в различных сферах деятельности; способность использовать приобретенные математические знания для решения задач в различных сферах; готовность применять математику в различных ситуациях. Одной из оставляющей функциональной грамотности – это математическая грамотность учащихся. Математическая грамотность – это способность человека определять и понимать роль математики в мире, в котором он живёт, высказывать обоснованные математические суждения и использовать математику так, чтобы удовлетворять в настоящем и будущем потребности, присущие созидательному, заинтересованному и мыслящему гражданину. В международном исследовании PISA (Programme for International Student Assessment) термин «функциональная математическая грамотность» означает «способность учащегося использовать математические знания, приобретенные им за время обучения в школе, для решения разнообразных задач межпредметного и практико-ориентированного содержания, для дальнейшего обучения и успешной социализации в обществе». Один из самых важных и сложных вопросов математики это «Развитие функциональной грамотности учащихся». Сейчас об том много говорят. Функциональная грамотность – это модное новое слово. Но на самом деле- это ключевые умения, которые позволяют решать нерафинированные задачи, а наоборот, использовать математические методы, чтобы решать задачи, которые возникают из практики, решать задачи, с которыми мы сталкиваемся в жизни. К сожалению, в учебниках, математики предлагается большое количество технических упражнений, а задач практического содержания очень мало, а ведь практические задачи более сложные и трудоемкие. Хочется продолжить выступление словами ученого математика Н. И. Лобачевского: « Математике должно учить еще с той целью в школе, чтобы познания здесь приобретаемые, были достаточными для обыкновенных потребностей жизни». Каждому человеку в своей жизни приходится выполнять математические расчеты, пользоваться вычислительной техникой, находить в справочниках и применять нужные формулы, владеть практическими приемами геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять несложные алгоритмы и др. Требование ФГОС: подготовить выпускника, обладающего необходимым набором современных знаний, умений и качеств, позволяющих ему уверенно чувствовать себя в самостоятельной жизни, умеющего применять знания в реальных ситуациях. В ОГЭ, ЕГЭ и ВПР включены практико-ориентированные задания. Поэтому в настоящее время важно не только заучивание и знание теории, а способность применять знания на практике. Реализовать данное требование ФГОС на уроках математики помогают практико-ориентированные задачи. В качестве источника практико-ориентированных задач можно использовать задания, предлагаемые в тестах PISA, исследованиях TIMSS и в контрольно-измерительных материалах для итоговой аттестации выпускников основной и средней школы. Практико-ориентированная задача позволяет обучать школьников решать жизненные проблемы с помощью предметных знаний. Практико–ориентированная задача повышает интерес к предмету, способствует развитию любознательности и творческой активности. При решении таких задач дети сами ищут, сопоставляют, обобщают, делают выводы – одним словом, действуют. Однако, ни один учебник не может раскрыть всё многообразие связей школьного курса с производительным трудом, поэтому приходится дополнять предлагаемые в учебнике системы упражнений составленными задачами. Большое значение имеет привлечение школьников к отыскиванию примеров применения знаний, полученных на уроках, в жизненных явлениях. «Скажи мне - и я забуду. Покажи мне - и я запомню. Дай мне действовать самому - и я научусь». Эти слова мудрого Конфуция современны как никогда. Конечно, быстрее и легче показать, объяснить, чем позволить ученикам самим открывать знания и способы действий. Самостоятельно ставить цели, анализировать, сопоставлять, оценивать, а главное - не бояться ошибаться в поисках нового пути. Именно этому нужно учить в школе. Преодолевать трудности, выходить за границу собственных знаний – эти испытания воли, духа, ума в конечном итоге непременно подготовят учеников к большим испытаниям в большой жизни. И поэтому, сегодня урок– это время, когда дети сами ищут, спорят, сопоставляют, обобщают, делают выводы - одним словом, активно действуют. Решение практико-ориентированных задач на уроках математики должно иметь конкретные цели: - Научиться решать задачи, с которыми каждый из нас может столкнуться в повседневной жизни. - Доказать, что математика нужна всем, чем бы человек не занимался, какой бы профессией не овладевал, где бы не учился. - Готовиться к сдаче ОГЭ и к Единому Государственному Экзамену, в который входят практико-ориентированные задачи. Практико-ориентированные задачи способствуют: - Повышению качества математической подготовки учащихся; - Пониманию использования математики во всех видах деятельности человека; - Созданию предпосылок для творческой деятельности учащихся. Конечно, все задачи практического содержания не рассмотришь на уроке и в программах нет отдельной темы по решению прикладных задач. И тогда задумываешься о том, зачем и чему мы учим детей? Мы столкнулись с проблемой необходимости включения и составления практико-ориентированных задач и определения их места на уроках математики. И сегодня мы представлем вашему вниманию несколько приёмов решений практико-ориентированных задач нового типа на различных этапах и типов уроков. Для достижения правильности и беглости устных вычислений в течение всех лет обучения на каждом уроке математики необходимо выделять от 5 – 10 минут для проведения тренировочных упражнений в устных вычислениях. Устный счет стараюсь проводить на каждом уроке. Устный счет я провожу по разному: по карточкам - продолжите вычисления, закончите фразу, под диктовку учителя и т.д. Пример (5 класс). 1.Магазин открывается в 10 часов утра, а закрывается в 10 часов вечера. Обеденный перерыв длится с 15 до 16 часов. Сколько часов в день открыт магазин? Здесь ученик должен прочитать грамотно, внимательно, понять , что ему дано и что надо найти, ответить на поставленный вопрос. Так, напр., с 10 утра до 10 вечера – это 12 часов. 2.Вдоль дороги (по прямой) через каждые 2 метра высажено дерево, всего посадили 120 деревьев, найдите длину зеленого ограждения. Комментарий. Большинство учащихся мгновенно дает ответ 240 метров. Однако, это неправильный ответ. Решение. Построим простую геометрическую модель. Обратим внимание: точек – три, а отрезков – два. Построим аналогичные геометрические модели из трех, четырех точек. Замечаем, что количество точек на одну больше, чем отрезков, соединяющих соседние точки. По условию деревьев – 120 шт, отрезков между соседними деревьями - 119. Длина зеленой изгороди 2*119=238 м. Ответ: 238 м длина зеленой изгороди. 3. Братья пилят бревно. Они сделали 10 распилов. Сколько получилось чурбачков? Ответ: 11 чурбачков. Пример (6 класс). Спидометр на велосипеде у Саши показывает 250, однако не уточняет единицу измерения. В чем измеряется скорость на спидометре Сашиного велосипеда? Выберите подходящий момент и обоснуйте. м/с 2) км/ч 3) м/мин 4) км/мин Перевод 10 м/с в … км/ч и наоборот Пример (7 класс-ВПР задания №5) При закреплении темы "Обозначение десятичных дробей" ученикам предлагается таблица:
Даются задания: 1) Назови и покажи числа в возрастающем порядке. 2) Назови и покажи числа в убывающем порядке. 3) Увеличь на 0,1 числа первой строчки (назови последующее). 4) Уменьши на 0,1 числа второй строчки (назови предыдущее). 5) Покажи числа, в которых сумма цифр в разряде десятых и единиц равна 6) Найди числа, в которых 7 (5, 8, 9) сотых. 7) Найди числа, в которых 4 (2, 3) десятых 8) Найди числа, в которых количество единиц на 2 (на 3, на 4) больше количества десятых. 9) Найди числа, в которых количество единиц равно количеству десятых. 10) Найди числа, в которых количество единиц десятых меньше количества сотых и т.д. Работу можно проводить в виде соревнования: "Кто быстрее?", "Какой ряд сделает меньше ошибок?" Эту же таблицу можно использовать и на последующих уроках с заданиями: 1) Увеличь числа второй строчки на 3. 2) Прибавь 2 к числам третьей строчки. 3) Увеличь числа четвертой строчки на 1 десяток. 4) Вычти 1 из чисел пятой строчки. 5) Прибавь 0,2 к числам первого столбика. 6) Вычти 0,2 из чисел второго столбика 7) Сложи числа первой и второй строчки, запиши ответы. 8) Из чисел третьей строчки вычти числа пятой строчки. 9) Дополни числа четвертой строчки до ближайшего круглого числа. В практике распространены таблицы с использованием математических терминов
Такие таблицы помогают детям лучше понимать математическую речь, лучше ориентироваться в терминах. Работа с такими таблицами готовит учеников к решению уравнений. Работа с таблицами нравится ученикам, поэтому она также нашла свое место на моих уроках математики. При повторении изученного материала по теме «Признаки делимости», предлагаю таблицу
Предлагаются задания: 1) Выберите из таблицы числа, которые делятся на 2 (3,5 и т.д.) 2) Разделите числа из первого столбика на 5 (2, 3) 3) Уменьшите числа последнего столбика в 9 раз. 4) Найдите «лишнее» число во втором столбике. 5) Найдите числа, которые не использовали А теперь перейду непосредственно е практико-ориентированным задачам. Следующую задачу можно предложить поработать по материалам огэ в разных классах. По изучению соответствующих тем составлять вопросы. Примеры (5-11 классы). 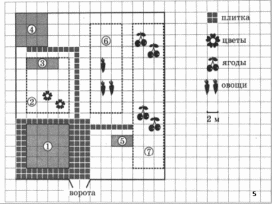 На плане изображен дачный участок по адресу: СНТ Рассвет, ул. Морская, 7 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Въезд и выезд осуществляется через единственные ворота. Площадь, занятая жилым домом, равна 64 кв. м. Помимо жилого дома, на участке есть баня, к которой ведет дорожка, выложенная специальным садовым покрытием. Между жилым домом и баней находится цветник с теплицей. Теплица отмечена на плане цифрой 3. Напротив жилого дома находится бак с водой для полива растений, за ним плодово-ягодные кустарники. В глубине участка есть огород для выращивания овощей, отмеченный цифрой 6. Все дорожки внутри участка имеют ширину 1 м и застелены садовым покрытием, состоящим из плит размером 1м х 1м. Площадка вокруг дома выложена плитами такого же размера, но другой фактуры и цвета. К дачному участку проведено электричество. Имеется магистральное газоснабжение. Вопросы для устной работы: Какими цифрами на плане обозначены: жилой дом, цветник, бак с водой, баня. Назовите получившееся число. Найдите площади этих объектов. На сколько площадь занятая под ягоды, больше площади занятой под овощи? Рассмотрим приемы решения практико-ориетированных задач (см. слайд): Разбор задач Задачи о дачном участке Задачи о земледелии в горных районах Задачи о мобильном интернете и тарифе Задачи о теплице Задачи про шины Задачи про форматы листов |
