Системый анализ. Системный анализ. Вопросы к экзамену.. Редакторы и вопросы (желательно вписывать по порядку)
 Скачать 212.55 Kb.
|
|
Дерево решения – это графическое представление последовательности решений и условий экономической среды, а также соответствующих вероятностей этих условий для любых желаемых комбинациях решений. В дереве решений различают узлы событий и узлы решений. В узлах событий выбор дальнейшего пути определяется внешними условиями (как говорят в теории игр, – природой), а в узлах решений – лицом, принимающим решение. Например, ЛПР может выбирать вариант реализации проекта по производству товара, а природа – реализовать высокий или низкий уровень спроса на данный товар. Деревья решений представляют собой иерархические структуры принятия решений, облегчающие понимание задачи и процесс выбора подходящего решения из нескольких. Дерево решений позволяет отразить временной ход процесса принятия решения и отдельные его этапы. Разбиение на этапы производят так, чтобы выбор решения начинался с момента принятия решения – узла решения, от которого исходят одна или несколько ветвей, представляющих альтернативные варианты. Далее следуют узлы случайных событий, и на конце – «листья», конечные состояния с указанием значений соответствующих выходных параметров (например, величин убытков, возможных прибылей, выигрышей и т. д.). Если же за узлами событий следует опять узел решений с соответствующими действиями, тогда он и все последующие разветвления относятся к более поздней стадии выбора решения. Таким образом, можно проследить весь путь с начала до конца дерева решений. Деревья решений легко поддаются модификации: при необходимости их можно дополнительно развить, а в случаях, когда какие-либо ветви практически лишены значения, – соответственно уменьшить. Узлы решений, если они связаны с одним действием и не разделены узлами событий, могут быть при необходимости объединены. То же справедливо и для узлов событий. Риски зависят от рассматриваемых задач! (Финансовые риски, риски оценки сроков, риски персонала, коммерческие риски и прочие) B общем случае для решения задачи предусматривается выполнение следующих этапов: 1. Постановка задачи. Требуется среди многих факторов, влияющих на решение проблемы, определить основные. Затем рекомендуется определить возможности по сбору необходимой информации, экспериментирования. Далее рекомендуется: составить перечень событий (состояний экономической среды или рынка), которые могут произойти c определенной вероятностью, установить временной порядок их возникновения и последовательность действий ЛПР. 2. Построение дерева решений. В виде логической структуры, обычно – слева направо (реже – сверху вниз) располагаются узлы принятия решения (часто представлены квадратами) узлы случайных событий (круги). 3. Оценка вероятностей состояний производится, исходя из имеющейся статистики, либо экспертным путем. 4. Оценка результатов (эффективности принятия решений) для каждой возможной комбинации действий инвестора и состояний рынка. Ценность каждой из возможных альтернатив рассчитывается как математическое ожидание с учетом вероятности состояний природы. 5. Окончательный выбор. Находим наиболее подходящую альтернативу, причем, если таковых несколько, желательно ограничиться альтернативой с меньшим числом промежуточных узлов, либо уточнить задачу, рассмотрев дополнительные факторы влияния. 16.Предмет теории игр.Примеры игровых ситуаций.Определение и основные признаки игры с несовпадающими интересами.(Чем занимается?(процессы принятия решений в конфликтных ситуациях.)(примеры: выборы, тендеры, (пример с лекций))(Определение) Теория игр рассматривается также как теория принятия оптимальных решений в условиях неопределенности. Она позволяет «математизировать» некоторые важные аспекты принятия решений в технике, сельском хозяйстве, медицине и социологии. Перспективен подход с позиций теории игр к проблемам управления, планирования и прогнозирования Целью теории игр является выработка рекомендаций по рациональному образу действий участников в конфликтных ситуациях, то есть определение оптимальной стратегии каждого из них. Практическое значение теории игр состоит в том, что она служит основой моделирования игровых экспериментов, в частности, деловых игр, позволяющих определять оптимальное поведение в сложных ситуациях. Характерной особенностью так называемых конфликтных ситуаций является то, что ни одна из участвующих сторон (в матричных играх их две) не знает заранее решения, которое будет принято соперником, следовательно, каждый вынужден действовать в условиях неопределенности. Математическая теория игр дает научно обоснованные рекомендации поведения в конфликтных ситуациях и ситуациях с неопределенностью, показывая, «как играть, чтобы не проиграть». Она дает формальный язык для описания процессов принятия сознательных, целенаправленных решений с участием одного или нескольких лиц в условиях неопределенности и конфликта, вызываемого столкновением интересов конфликтующих сторон. В одних ситуациях противоположной стороной выступает сознательно и целенаправленно действующий активный противник, заинтересованный в нашем поражении, который сознательно препятствует успеху, добивается победы любыми средствами. Это антагонистические игры, которые в рамках данного пособия не рассматриваются. В других ситуациях принятия решения такого сознательного противника нет, а действуют лишь так называемые «слепые силы природы»: погодные условия, состояние торгового оборудования на предприятии, болезни сотрудников, нестабильность экономической ситуации, рыночная конъюнктура, динамика курсов валют, уровень инфляции, налоговая политика, изменяющийся покупательский спрос и т.п. В таких случаях «природа» не злонамеренна и выступает пассивно (реализуя определенные обстоятельства, условия принятия решения), иногда во вред человеку, а иногда к его выгоде, однако ее состояние и степень проявления негативных/позитивных факторов могут ощутимо влиять на результат деятельности. В ситуациях подобного рода выбор решения зависит от состояний объективной экономической действительности, называемой в модели «природой». Данный термин характеризует некую объективную действительность, которую не следует понимать буквально. Математические модели подобных ситуаций называются “играми с природой” ПРИМЕРЫ ИГР И ДОП. ИНФА (Кликабельно. Спасибо Сергею Сёмкину за запись лекции) 17.Принятие решений в условиях неопределённости. Понятие игры с природой. Платежная матрица игры с природой. Матрица Рисков.(примеры неопределенностей.Трудность принятия решений в том что не всё зависит от тебя. определение. нарисовать матрицы и объяснить как формируется матрица рисков) В игре с природой сознательно действует только один из участников, в большинстве случаев называемый игроком один. Игроку два (природа) не важен результат, либо он не способен к осмысленным решениям. Или, возможно, условия не зависят от действий игрока, а определяются внешними факторами: реакция рынка, который не будет вредить одному конкретному игроку, государственная политика, реальная природа.  ← Платежная матрица игры с природойМатрица риска - это таблица или диаграмма, которая отображает значимость события на одной оси, и вероятность его возникновения на другой. Промежуточным итогом этой работы должен стать план реагирования. По матрице можно сделать выводы, направленные на улучшение развития компании. Виды неопределенностей (примеры) - количественная, обусловленная значительным числом объектов или элементов в ситуации; - информационная, вызванная недостатком информации или ее неточностью по техническим, социальным и другим причинам; - стоимостная, из-за слишком дорогой или недоступной платы за определенность; - профессиональная как следствие недостаточного профессионализма лица, принимающего решение; - ограничительная (вызванная ограничениями в ситуации принятия решений, например ограничения по времени и др.); - внешней среды, связанная с ее поведением или реакцией конкурента на процесс принятия решения. Пример матрицы рисков:  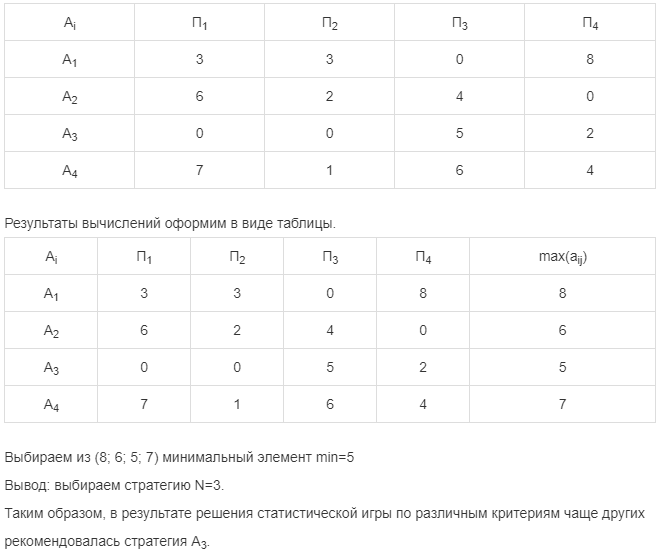 18.Критерии Вальда и максимакса в играх с природой. Критерий Вальда (максимина) - Пессимистический критерий. Формула: ( 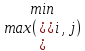 ). Игрок рассматривает наихудшие сценарии развития событий и делает выбор в пользу того, чей наихудший сценарий является наименее пессимистическим в сравнении с остальными или “лучшим среди худших”. Для данной матрицы, следуя критерию Вальда, ответ - 
Критерий максимакса - Оптимистический критерий, противоположный критерию Вальда. Формула: ( 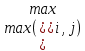 ). Игрок надеется на лучшее, и, поэтому, выбирает альтернативу, чей наилучший сценарий больше и лучше остальных. Для данной матрицы, следуя критерию максимакса, ответ - 
19.Критерии Байеса и Лапласа Критерий Байеса (выбор в условиях определенности) - Критерий подразумевает, что игроку известны вероятности поведения природы. То есть для каждого П есть q, выражающая вероятность соответствующего П. Выгода каждой из возможных альтернатив выражена соответствующим ей мат. ожиданием, которое вычисляется для каждой строки, затем полученные значения сравниваются. Выбирается альтернатива с наибольшим мат. ожиданием. Мат ожидания для данной таблицы (вероятности подписаны в верхней строке) мат. ожидания для  = (18*0.3)+(8*0.6)+(-2*0.1) = 10мат. ожидания для = (6*0.3)+(36*0.6)+(26*0.1) = 26 (Ответ)мат. ожидания для 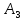= (-6*0.3)+(24*0.6)+(54*0.1) = 18Таким образом, в соответствии с критерием Байеса, ответ:
Критерий Лапласа (выбор в условиях неопределенности) - Критерий Лапласа абсолютно идентичен критерию Байеса лишь за тем исключением, что нам неизвестны вероятности поведения природы. Поэтому, в соответствии с этим критерием, мы признаём их равновероятными (т.е. при 3 различных сценариях поведения природы, q = 0,33 для каждого из них). После этого для каждой альтернативы поведения игрока вновь вычисляются их мат. ожидания и на основе этого, делается выбор в пользу одной из альтернатив. мат. ожидания для 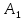= (18*0.33)+(8*0.33)+(-2*0.33) = 8мат. ожидания для = (6*0.33)+(36*0.33)+(26*0.33) = 22,67мат. ожидания для 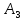= (-6*0.33)+(24*0.33)+(54*0.33) = 24 (Ответ)Таким образом, в соответствии с критерием Лапласа, ответ: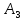
|
