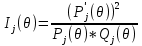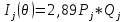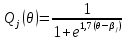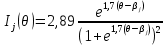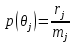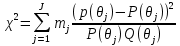Реферат 1 Введение 3 Аналитическая часть 5
 Скачать 1.24 Mb. Скачать 1.24 Mb.
|
Характеристический кривые, информационная функцияДля графического описания полученных результатов служат так называемые характеристические кривые заданий ICC (Item Charaсteristic Curves). Существует 2 вида кривых: первые описывают зависимость вероятности правильного ответа на задание для испытуемых с различным уровнем подготовленности (Pj), вторые - зависимость вероятности правильного ответа студента на задания с различными уровнями трудности (Pi). На рисунке 10 представлены кривые трех заданий с уровнями трудности β равным -2, 0, и 2 логита для студентов с уровнями подготовленности от -5 до 5 логит. Обычно рассматривают именно этот диапазон (от -5 до 5 логит), потому что для θ<-5 Pj стремится к 0, а для θ>5 - к единице. 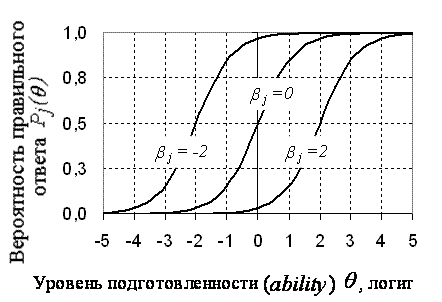 Рисунок 10 - Характеристические кривые заданий Источник:[15] На рисунке 11 представлены кривые трех испытуемых с уровнями подготовленности θ равными -2, 0 и 2 логита в зависимости от трудности задания в интервале от -5 до 5 логит. Здесь обычно используется диапазон значений аналогичен предыдущему случаю. 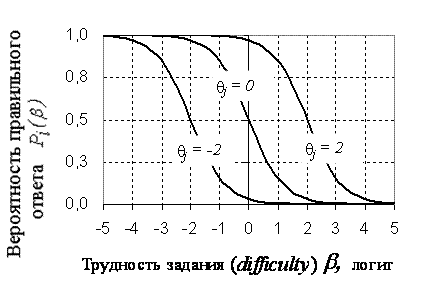 Рисунок 11 - Характеристические кривые испытуемых Источник: [17] Графический образ задания,меняется в зависимости от значений параметров aj (дифференцирующая способность задания для двухпараметрической модели) и сj (вероятность угадывания правильного ответа для трехпараметрической модели). На рисунке 12 задание, расположенное справа, труднее и имеет сравнительно большую различающую способность. 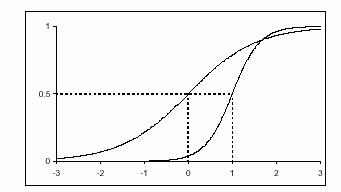 Рисунок 12 - Характеристические кривые заданий, имеющих различную дифференцирующую способность Источник:[17] Влияние параметра аjна графики двух заданий разного уровня трудности представлено на рисунке 13. Чем больше значения аj, тем круче выглядит график задания. Соответственно, «крутыми» иногда называют и задания. То есть значение параметра аj выражается крутизной характеристической кривой задания, аналитически – значением производной функции в точке перегиба[22]. На рисунке 13 представлены графики заданий, имеющих одинаковый средний уровень трудности, но имеющих неодинаковую меру различающей способности. 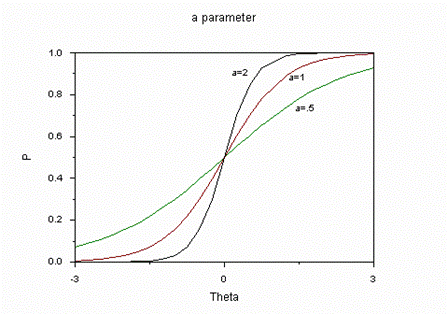 Рисунок 13 - Характеристические кривые одного задания с разным значением дифференцирующей способности Источник:[15] Для рассматриваемого примера рассчитаем Pj - вероятность верного ответа на j-ое задание по однопараметрической модели Раша и построим характеристические кривые заданий 12 (рисунок 14) и 20 (рисунок 15). Рисунок 14 - Характеристическая кривая 12 задания с уровнем сложности β = 0,39721 Рисунок 15 - Характеристическая кривая 20 задания с уровнем сложности β = -2,32045 Для задания 12 уровень сложности равен 0,39721 - очень близкий к 0. Точка перегиба характеристической кривой находится на уровне θ = 0 логит и Pj = 0,5 логит, что соответствует заданию со средним уровнем трудности. То есть испытуемые с уровнем подготовленности 0 (что говорит о том, что эти учащиеся не "слабые", но и не отличники) ответят на данный вопрос с вероятностью 50%. В то время как вероятность верного ответа у "слабых" учеников (θ < -2,5 логит) близка к 0, а у "сильных" (θ > 2,5 логит) юлизка к единице. Другую картину наблюдаем у задания с номером 20. Это простое задание, потому что кривая смещена влево - вероятность верного ответа у испытуемых со средним уровнем подготовленности (θ = 0 логит) составляет примерно 0,9 логит. Информационная функция и методы её расчёта являются важной частью научного аппарата IRT. Это понятие и метод вычисления ввёл А. Бирнбаум. Количество информации, обеспеченное j-м заданием теста в данной точке θi - это величина, обратно пропорциональная стандартной ошибке измерения данного значения θi с помощью j-го задания. Для описания информации, соответствующей заданию вводится информационная функция I(θ):
где Ij(θ) - информационная функция от латентной переменной величины θ, Pj' - производная величины Pj, Qj - вероятность неверного ответа на j-ое задание в точке θ. Для однопараметрической модели Pj' = 1,7 PjQj, тогда
где Qj(θ) =1 - Pj(θ). То есть
Тогда формула (30) приобретает следующий вид:
Информационная функция свидетельствует о количестве информации, которое даёт каждое задание для измерения уровня подготовленности каждого испытуемого. Это количество зависит от значений близости оценок уровня подготовленности испытуемых и трудности задания. Чем ближе эти значения, тем более информативно (эффективно) задание для измерения уровня подготовленности испытуемых именно такого уровня подготовленности[15]. Для каждой модели измерения используется своя информационная функция. Для данных, представленных в дихотомической шкале (1/0) для модели Раша максимальное значение информационной функции равно 0,25. Это значение получается для заданий, имеющих среднюю меру трудности (p = q = 0,5). Тогда произведение p*q = 0,25. Если для данных модели Раша графики задания и информационной функции расположить на одной плоскости (рисунок 16) , то чёрная линия – это график задания, синяя линия- график информационной функции задания. Красная линия указывает на проекции точки перегиба функции на ось абсцисс и ось ординат. 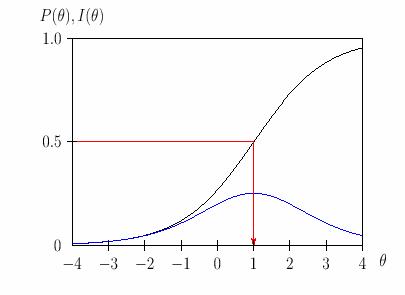 Рисунок 16 - Характеристическая кривая и информационная функция одного задания Источник:[15] Максимум информации задание даёт для измерения уровня подготовленности испытуемых, у которых этот уровень в точности равен уровню трудности задания. Чем больше отличаются значения этих двух показателей, тем задание менее информативно с точки зрения эффективности измерения. Интерпретация графика информационной функции столь же проста, сколь и эффективна для разработчика теста: чем больше значение I(θi), тем лучше тест измеряет. Максимум информации при измерении знаний испытуемых получается в той точке, где I(θi) принимает максимальное значение. В таких случаях можно говорить, что тест разработан для измерения знаний студентов с уровнем , где I(θi) принимает значение максимума. Там, где значение I(θi) минимально, можно определенно говорить о неэффективности теста для измерения знания у студентов с соответствующей подготовкой. Информационная функция в IRT считается не только для отдельного задания, но и для теста в целом. Для этого надо суммировать количество информации, даваемое в интересующей точке θi каждым заданием. Определение информационной функции теста для каждой интересующей точки оси тета даёт возможность целенаправленной разработки такого теста, который позволяет решать задачи, например, профотбора. Если надо отобрать половину лучших, то точность измерения повышают на уровне средней подготовленности, где и применяется данное решающее правило. В таких случаях в тест добавляют задания среднего уровня трудности. Но тогда очень плохо измеряется подготовка сильных и слабых испытуемых. Если нужно, чтобы тест был эффективен на всём интересующем диапазоне подготовленности испытуемых, то задания теста стараются подобрать равномерно возрастающей трудности. Учебный пример такого рода равномерного подбора заданий «теста», состоящего всего из пяти заданий представлен на рисунке 17. 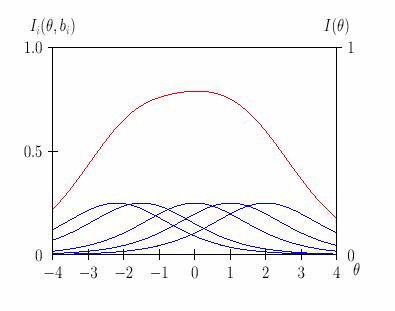 Рисунок 17 - Информационная функция каждого задания и теста "в целом" Источник:[15] Для нашего примера построим график информационной функции для каждого задания и теста "в целом". На рисунке 18 видно, что информационные функции зданий располагаются довольно равномерно по всей оси тета. Это значит, что тест эффективен для испытуемых с уровнями подготовленности из всего диапазона и его максимум достигается в точке θ = 0. Рисунок 18 - Информационная функция рассматриваемого примера Обработка полученных результатовПедагогический тест, как средство измерения учебных достижений, может дать достоверный результат только в случае его корректного применения. Корректность применения теста – это многоаспектное понятие, включающее в себя вопросы конструирования и дизайна теста, вопросы разработки и применения тестов и, разумеется, интерпретации результатов тестирования. Таким образом, несоответствие эмпирических данных модели Раша означает, что, например, имеются неточности в формулировке заданий, были нарушения в процедуре тестирования и т.д. При анализе результатов тестирования, нужно проверить соответствие эмпирических данных данным, рассчитанным по модели Раша. Согласно Ф. Бейкеру[23] для этого всех N тестируемых, выполняющих M заданий теста распределяют по шкале θ (ability) по своим диапазонам уровня подготовленности. Испытуемые делятся на J групп вдоль шкалы θ так, чтобы все тестируемые внутри данной группы имели одинаковый уровень подготовленности θj. Осуществить это можно с помощью любого алгоритма кластеризации, с заданным количеством кластеров. Всего внутри группы с номером j окажутся mj тестируемых, где j принимает значения из интервала j = 1,2,3,…,J. В пределах каждой группы rj тестируемых отвечают правильно на данное задание теста. Таким образом, для уровня подготовленности (уровня знаний) равного θj вероятность правильного ответа на данное задание равна
где rj - количество верно ответивших на задание в пределах группы j, mj - количество учащихся, попавших в j-ую группу, j = 1,2, .. , J, p(θj) - экспериментальное значение вероятности правильного ответа на данное задание. Далее необходимо проверить, насколько хорошо эмпирические данные описываются моделью. Для проверки гипотезы Ho на соответствие полученных эмпирических данных одномерной модели IRT для всех заданий теста проводилось вычисление критерия χ2 согласно Ф. Бейкеру[24]:
где p(θj) - экспериментальное значение вероятности правильного ответа на данное задание, P(θj) - теоретическое значение вероятности правильного ответа на данное задание, рассчитанное по модели Раша, Q(θj) - теоретическое значение вероятности неправильного ответа на данное задание. Рассчитанное значение ��2 позволяет судить о степени соответствия экспериментальных данных модели Раша. По нему можно рассчитать квантиль распределения ��2 - α. Значение квантиля находится в диапазоне от 0 до 1. Чем ближе значение α к единице, тем лучше согласие между экспериментальными данными и теоретическими, рассчитанными по модели. Соответственно, чем ближе значение к нулю, тем хуже согласие. Критическое значение равняется - 0.05. Для расчета Необходимы рассчитанное значение ��2 и количество степеней свободы (размерность вектора случайной величины), которое в нашем случае будет - J. Далее определяем квантиль и по нему определяем - согласуются ли экспериментальные данные с теоретическими. Проверим данные нашего примера. Выборка студентов небольшая, поэтому поделим их на три группы следующим образом (таблица 12): Таблица 12 - Распределение студентов на группы по уровню подготовленности
Для анализа возьмем задание №7 и №20. Рассчитаем для них экспериментальные данные (таблица 13). Таблица 13 - Экспериментальные данные для задания №20 и №7
Далее по формуле (34) рассчитаем значение ��2. Для задания №20 оно равняется 1,346, что соответствует квантилю 0,7, для задания №7 - 0,443, α = 0,9. То есть задание №20 имеет хорошее согласие с моделью Г. Раша, а задание №7 - отличное согласие. Построим графики характеристических кривых рассматриваемых заданий и нанесем на них экспериментальные точки, чтобы проиллюстрировать полученные аналитически результаты. На рисунке 19 на график характеристической кривой задания добавлены экспериментальные данные. Видно, что присутствует аномалия - испытуемые с низким уровнем подготовленности отвечают на данное задание лучше, чем испытуемые со средним уровнем. Это может быть связано какими-либо нарушениями в ходе тестирования. Но аномальный эффект проявляется частично (α > 0,05), поэтому данное задание можно оставить в тесте. Рисунок 19 - Экспериментальные данные на графике характеристической кривой 20-го задания Из рисунка 20 видно, что эмпирические точки практически лежат на характеристической кривой, что говорит о том, что экспериментальные данные имеют отличное согласие с теоретическими данными, рассчитанными по модели Г. Раша. Рисунок 20 - Экспериментальные данные на графике характеристической кривой 7-го задания Алгоритм кластеризации данных k-meansВ предыдущем разделе, при построении характеристической кривой задания возникла необходимость в разбиении набора двухмерных точек на несколько групп, в которых значения этих точек будут примерно одинаковым. Исходя из этого, в рамках дипломной работы возникла задача кластеризации данных. Предполагается, что разбиение этих точек на группы будет проходить на основании одномерных величин. К тому-же, количество групп заранее известно. Так-же, не предполагается сверх-большого количества разбиваемых точек(оно соответствует количеству студентов, прошедших тест). Потому, для выполнения этой задачи был выбран алгоритм кластеризации k-means из семейства алгоритмов квадратичной ошибки, который обладает достаточной эффективностью и простотой для текущей задачи. Задачу кластеризации можно рассматривать как построение оптимального разбиения объектов на группы. При этом оптимальность может быть определена как требование минимизации среднеквадратической ошибки разбиения: где cj — «центр масс» кластера j (точка со средними значениями характеристик для данного кластера). Алгоритм k-means строит заданное число кластеров, расположенных как можно дальше друг от друга. Работа алгоритма делится на несколько этапов:
В качестве критерия остановки работы алгоритма обычно выбирают минимальное изменение среднеквадратической ошибки. Так же возможно останавливать работу алгоритма, если на шаге 2 не было объектов, переместившихся из кластера в кластер. |