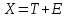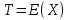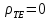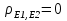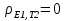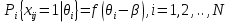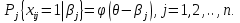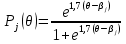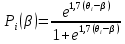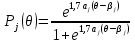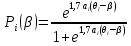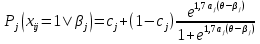Реферат 1 Введение 3 Аналитическая часть 5
 Скачать 1.24 Mb.
|
Современная теория тестов и ее модели оценки знанийОсновы классической теории тестов (КТТ) заложены в трудах британского психолога Чарльза Эдварда Спирмена[13] (Charles Edward Spearman) (1863-1945 г.), опубликованных с 1904 по 1913 годы, в которых он обосновал, что тестовые оценки характеристик людей всегда содержат ошибочные компоненты измерения. Всякий раз, когда испытуемый выполняет тест, его оценку по этому тесту можно рассматривать как значение случайной переменной. На результат выполнения оказывают влияние самые разные факторы - невнимательность, случайное удачное или неудачное угадывание ответов, неправильного прочтение условия задачи и т.д. Представим ситуацию, когда испытуемому много раз предъявляют один и тот же тест, при условии, что он не устает при его выполнении и полностью забывает задания после предыдущего тестирования. Очевидно, что наблюдаемые оценки, полученные при повторном тестировании этого испытуемого, будут колебаться из-за ошибок измерения, рассмотренных ранее. Истинную оценку (истинный балл) испытуемого можно интерпретировать как среднее значение наблюдаемых оценок, полученных по бесконечному числу повторяющихся тестирований при использовании одного и того же теста. Так как преподаватель имеет дело только с фактически полученными результатами измерения, то в процессе создания и применения тестов всегда стоит задача не получить истинные баллы, а лишь как-то приблизиться к их наиболее достоверным оценкам [14]. Ошибка измерения также является случайной величиной и представляет собой разность между наблюдаемой тестовой оценкой испытуемого (случайной величиной) и его истинной оценкой. Таким образом, в теории педагогических измерений ошибка трактуется как статистическая величина, отражающая степень отклонения наблюдаемого балла от истинного балла ученика. Ошибки измерения происходят по различным как контролируемым, так и неконтролируемым причинам и дифференцируются в зависимости от источника происхождения. Среди различного рода ошибок можно выделить два наиболее важных типа: систематические и случайные [10]. К систематическим относятся ошибки, порождаемые недостаточным качеством теста и/или неправильными условиями его проведения. Это те погрешности, которые неизбежно привносит любой разработчик теста в процесс создания и применения средства измерения. Например (помимо плохого качества заданий), к систематическим ошибкам может привести отсутствие качественной аппаратуры для прослушивания текстов на экзамене по иностранному языку. Случайные ошибки происходят от особенностей поведения испытуемых, а не от заданий теста. Испытуемый может плохо себя почувствовать в процессе выполнения теста. Для некоторых в помещении слишком жарко или холодно. На результаты тестирования влияют скука, усталость либо волнение. Ученик может ошибаться при осмыслении формы задания или неверно понять инструкцию и по этим причинам указать неправильный ответ. С другой стороны, могли иметь место нарушения процедуры тестирования, например, отдельным учащимся могла быть оказана помощь. В целом ошибки измерения влияют в ту или иную сторону на результаты тестирования, снижая надежность теста, которую рассматривают всегда исключительно в контексте случайных ошибок измерения. Классическая теория тестов основывается на следующих пяти основных положениях[15].
Величины T и E обычно неизвестны.
В группе сильных, хорошо подготовленных испытуемых, результаты тестирования будут, как правило, лучше, чем в группе слабо подготовленных испытуемых. В этой связи остается открытым вопрос о величине меры трудности заданий на генеральной совокупности испытуемых. Проблема заключается в том, что реальные эмпирические данные получают на вовсе не случайных выборках испытуемых. Как правило, это учебные группы, представляющие собой множество учащихся достаточно сильно взаимодействующих между собой в процессе учения и обучающиеся в условиях, часто не повторяющихся для других групп. Item Response Theory (IRT) – английское название теории, используемой преимущественно в педагогических и психологических измерениях. Общим источником для создания IRT послужила так называемая логистическая функция вид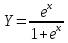а  , известная в биологической науке с 1844 года. С тех пор как она широко применялась в биологии для моделирования прироста растительной массы или роста организмов. Как модель психологического и педагогического измерения она начала применяться, начиная с 50-х годов ХХ столетия. У истоков развития моделей IRT лежали стремление визуализировать формальные характеристики тестовых заданий, попытки преодолеть многочисленные недостатки классической теории тестов, повысить точность измерений и, наконец, стремление оптимизировать процедуру контроля за счет адаптации теста к уровню подготовленности студента с помощью компьютера.В числе первых предпосылок к созданию IRT стали те результаты исследовательской работы A.Binet и T.Simon, в которых было отражено стремление авторов вывить как "работают" те задания, которые они давали детям разного возраста. Расположив затем на координатной плоскости точки, где по оси абсцисс отскладывался возраст в годах, а по оси ординат - доля правильных ответов в каждой возрастной группе испытуемых, авторы увидели, что полученные точки, после усреднения по каждой группе, напоминают кривую, позже названной характеристической [16]. IRT является психолого-педагогическим вариантом более общей методологии латентно-структурного анализа, развивавшегося, главным образом, в лабораториях военных ведомств США и университетов. Латентно-структурный анализ (от англ. Latent Structure Analyses, LSA) нацелен на выявление латентных качеств (факторов) поведения посредством математико-статистических моделей измерения [16]. Латентныминазываются интересующие положительные и отрицательные качества личности, не поддающиеся непосредственному измерению[17]. Примерами являются «подготовленность студентов», «знание учебной дисциплины», «способность понимать» «интеллектуальное развитие» и многое другое. Попытки измерения подобных качеств личности на уровне обыденного сознания оканчиваются словесными или численными оценками, содержащими в себе немалые погрешности. Идея и методы измерения латентных качеств реализуются в тесной зависимости от эмпирических результатов. Именно на основе реально наблюдаемых данных ставится задача воссоздания непосредственно ненаблюдаемого качества, измеряемого с помощью модели. О величине латентного параметра можно судить по ее индикатору (индикаторной переменной). Главное достоинство индикатора – его доступность для прямого наблюдения. Измеряя значение индикатора, мы можем судить о значении латентного параметра, с которым он связан. Например, индикатором может являться тестовое задание. Значением индикатора является числовое (символьное) выражение реакции испытуемого, на это тестовое задание. По этому индикатору мы можем судить об уровне знаний, соответствующих данному тестовому заданию. Индикатор – это некоторое средство воздействия (вопрос, тестовое задание), связанный с определенным латентным параметром, реакция на который, доступна для непосредственного наблюдения. Основные допущения IRT:
Основной задачей IRT является переход от индикаторных переменных к латентным параметрам[16]. В отличие от классической теории, где индивидуальный балл тестируемого рассматривается как постоянное число, в IRT латентный параметр трактуется как некоторая переменная. Начальное значение параметра получается непосредственно из эмпирических данных тестирования. Переменный характер измеряемой величины указывает на возможность последовательного приближения к объективным оценкам параметра с помощью тех или иных итерационных методов. В рамках основного предположения IRT устанавливается связь между латентными параметрами испытуемых и наблюдаемыми результатами выполнения теста. При установлении связи важно понимать, что первопричиной являются латентные параметры. Если говорить точно, то взаимодействие двух множеств значений латентных параметров порождает наблюдаемые результаты выполнения теста. Элементы первого множества – это значения латентного параметра, определяющего уровень подготовки N испытуемых qi (i = 1, 2, .., N). Второе множество образуют значения латентного параметра bj (j = 1, 2, …, n ), равные трудностям n заданий теста. Однако на практике всегда ставится обратная задача: по ответам испытуемых на задания теста оценить значения латентных параметров q и b. Для ее решения нужно ответить по меньшей мере на два вопроса. Первый связан с выбором вида соотношения между латентными параметрами q и b. Идея установления соотношения принадлежит датскому математику Г. Рашу, который предложил ввести его в виде разности (q - b), предполагая, что параметры q и b оцениваются в одной и той же шкале. Ответ на второй вопрос, который является центральным в IRT, связан с выбором математической модели для описания рассматриваемой связи между латентными параметрами и наблюдаемыми результатами выполнения теста. В частности, можно рассматривать условную вероятность правильного выполнения i-м испытуемым с уровнем подготовки qi различных по трудности заданий теста, считая qi параметром i-го ученика, а b – независимой переменной. В этом случае условная вероятность будет функцией латентной переменной b:
Здесь xij = 1, если ответ i-го испытуемого на j-е задание верный; xij = 0, если ответ i-го испытуемого на j-е задание неверный. Аналогично вводится условная вероятность правильного выполнения j-го задания с трудностью bj различными испытуемыми группы. Здесь независимой переменной является q, а bj – параметр, определяющий трудность j-го задания теста:
Различают 3 основные модели современной теории тестов:
где и – независимые переменные для первой и второй функций соответственно.
Кроме прежних обозначений в этой модели появляются параметры ai и aj. Параметр aj был введен А. Бирнбаумом для характеристики дифференцирующей способности задания при измерении различных значений ; параметр ai указывает на меру структурированности знаний ученика.
где cjявляется третьим параметром модели, характеризующим вероятность правильного ответа на задание j в том случае, если этот ответ угадан, а не основан на знаниях ученика. В каждой из представленных моделей параметры и выражаются как шкалированные показатели единой для всех моделей шкалы логитов. При отношении двух величин, равном е, их различие составит 1 логит. Таким образом, получается шкала, в которой можно говорить, что знания двух испытуемых или трудности двух упражнений различаются на столько-то логит(а не во столько-то раз). Перечислим преимущества IRT перед классической теорией тестов:
|
