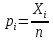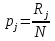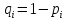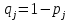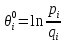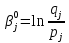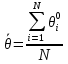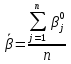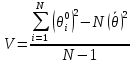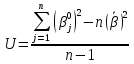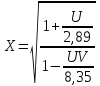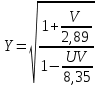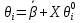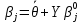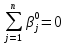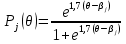Реферат 1 Введение 3 Аналитическая часть 5
 Скачать 1.24 Mb. Скачать 1.24 Mb.
|
Однопараметрическая модель Г. РашаВ данном разделе приводится описание алгоритма расчета оценки тестовых заданий по однопараметрической модели Г. Раша современной теории тестов. Для наглядности рассматривается тестовый пример расчета оценки по данной модели, приводятся полученные результаты и соответствующие выводы. Для расчета теоретической вероятности правильного ответа в разрезе задания или учащегося необходимо оценить следующие параметры:
Для наглядности рассмотрим пример: в классе 8 учащихся. Класс прошел тест, состоящий из 20 вопросов. Ответы на задания теста распределились следующим образом (1 - верный ответ, 2 - неверный ответ) (таблица 2): Таблица 2 - Бинарная матрица с результатами прохождения теста
Из бинарной матрицы ответов необходимо удалить строки и столбцы, в которых все ответы верные, т.к. они не показательны для анализа. В рассматриваемом примере отсутствуют столбцы и строки только с единицами, поэтому матрица не меняется. Для дальнейшего анализа, нам потребуются значения pi и qi – доли правильных и неправильных соответственно ответов i-го ученика на задания теста; pj и qj – доли правильных и неправильных ответов учеников на j-е задание теста, вычисленные по формулам:
где Xi - количество правильно выполненных заданий i-ым учеником, i = 1,2,..N, n - число заданий в тесте, Rj - количество правильных ответов на j-ое задание теста, j = 1,2,..,n, N - количество учащихся в группе.
Для рассматриваемого примера значения долей верных и неверных ответов будут следующими (таблицы 3 и 4): Таблица 3 - Доли верных и неверных ответов для заданий теста
Таблица 4 - Доли верных и неверных ответов для учащихся
Далее рассчитываются начальные значения параметров и находят по формулам:
В нашем примере значения данных параметров будут (таблицы 5 и 6): Таблица 5 - Начальные значения уровня трудности заданий 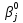
Таблица 6 - Начальные значения уровня подготовленности учащихся 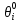
Затем начальные значения параметров переводятся в единую интервальную шкалу стандартных оценок. Стандартизация достигается с помощью ряда специальных преобразований, в ходе которых вычисляются среднее значение 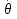 для множества для множества 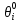 (i = 1, 2, …, N), среднее значение (i = 1, 2, …, N), среднее значение 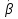 для множества для множества 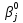 (j = 1, 2, …, n), дисперсии по этим множествам и поправочные коэффициенты X и Y. (j = 1, 2, …, n), дисперсии по этим множествам и поправочные коэффициенты X и Y.Средние значения:
Для нашего примера рассчитаем промежуточные данные для дальнейшего расчета (таблицы 7 и 8): Таблица 7 - Квадраты параметров 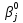 и среднего значения и среднего значения 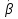
Таблица 8 - Квадраты параметров 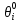 и среднего значения и среднего значения 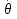
Далее рассчитываются оценки дисперсии:
Поправочные коэффициенты:
Для рассматриваемого примера получаем следующие значения оценок дисперсий и поправочных коэффициентов: Таблица 9 - Оценки дисперсий и поправочные коэффициенты
Оценки параметров и в единой интервальной шкале находятся по формулам:
Рассчитанные значения параметров и для рассматриваемого примера (таблицы 10 и 11): Таблица 10 - Оценки параметров уровня трудности заданий
Таблица 11 - Оценки параметров уровня подготовленности испытуемых
Роль последних двух формул в развитии современной теории тестов трудно переоценить, хотя на первый взгляд они имеют узкую практическую направленность. Эти формулы позволяют преодолеть ряд существенных недостатков классической теории тестов, поскольку с их помощью можно получить объективные оценки параметров испытуемых и заданий, не зависящие друг от друга и выраженные в единой интервальной шкале. Благодаря особенностям математического аппарата IRT проведенные расчеты обеспечивают объективные оценки уровня подготовки каждого испытуемого, не зависящие от трудности заданий теста. Отмеченное свойство инвариантности позволяет провести корректное сравнение результатов испытуемых, выполнивших различные по трудности задания теста и даже разные тесты [9]. Аналогичное преимущество существует в IRT и для оценок трудности заданий теста. Получаемые по алгоритмам значения параметра инвариантны относительно уровня подготовки испытуемых в тестируемой группе. Хотя теория обещает инвариантность, в силу действия различных случайных факторов оценки параметров и , полученные на нескольких выборках, будут, конечно, различаться. Если объем выборки достаточно велик, то можно ставить вопрос о вычислении устойчивых значений параметров и , которые будут наиболее эффективными оценками и могут быть приняты в качестве объективных значений и . Например, для вычисления таких эффективных оценок можно использовать метод наибольшего правдоподобия, предложенный Р.Фишером [7]. Тест считается удачно сбалансированным по трудности заданий, если
Далее на основе рассчитанных параметров уровня подготовленности учащихся и уровня трудности задания рассчитываются теоретические вероятности верного ответа для i-го учащегося или j-го задания теста по формулам (8) и (9).
В основном нас интересует только Pj. Эти данные используются далее в анализе адекватности вопроса, что будет более подробно рассмотрено в п.2.4. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||