Шеннон использовал метод дискретизации применительно к упомянутому выше доопределению B вида (3) функции одиночного сообщения f (t), которая считается нулевой для 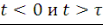 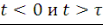 . Проблема решается в рамках следующего подхода. . Проблема решается в рамках следующего подхода.
Возьмем периодическую функциюf (t) с большим периодом 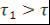 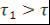 и будем считать, что и будем считать, что 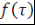 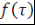 принимает свои значения на интервале от 0 до принимает свои значения на интервале от 0 до   и обращается в ноль на интервалеот и обращается в ноль на интервалеот  до до 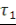 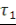 . .
При этом считаем, что имеет место плавный переход в ноль на обоих концах интервала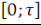 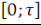 , чтобы не вносить каких-либо частот, лежащих выше границы , чтобы не вносить каких-либо частот, лежащих выше границы   . Новая функция дискретизируется на новом интервале . Новая функция дискретизируется на новом интервале 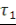 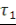 в в 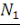 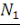 эквидистантных точках в соответствии с алгоритмом, выраженным формулами (9) и (13). Новый шаг дискретизации θ1 аналогичен (9): эквидистантных точках в соответствии с алгоритмом, выраженным формулами (9) и (13). Новый шаг дискретизации θ1 аналогичен (9):
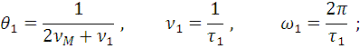 (17) (17)
Если   и и 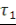 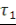 являются большими, то соответствующие частоты являются большими, то соответствующие частоты   и и 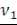 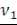 пренебрежимо малы по сравнению с максимальной частотой пренебрежимо малы по сравнению с максимальной частотой   , и мы получаем , и мы получаем
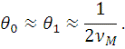
Полное число точек дискретизации определяется теперь формулой
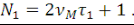 (18) (18)
Из этих 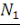 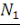 дискретных точек, дискретных точек,   точек попадают в интервал точек попадают в интервал 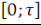 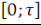 , а оставшиеся , а оставшиеся 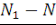 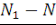 точек - в интервал точек - в интервал 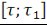 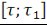 . Первый набор точек дает ненулевые дискретные значения: . Первый набор точек дает ненулевые дискретные значения:
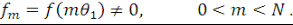 (19) (19)
Тогда как другие точки дают ноль:
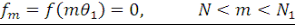
Импульсная функция  уравнения (13) принимает вид уравнения (13) принимает вид
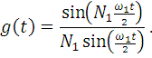 (20) (20)
Устремляя теперь 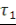 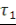 к бесконечности и, соответственно к бесконечности и, соответственно 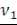 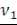 к нулю, мы получаем предельное значение для шага дискретизации: к нулю, мы получаем предельное значение для шага дискретизации:
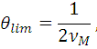
А также имеем бесконечное число дискретных значений   равных нулю. Единственные ненулевые значения соответствуют интервалу равных нулю. Единственные ненулевые значения соответствуют интервалу
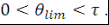
Их число определяется выражением
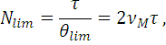 (21) (21)
что соответствует формуле (1), в то время как импульсная функция  упрощается и принимает вид упрощается и принимает вид
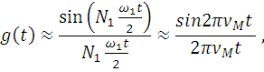 (22) (22)
поскольку
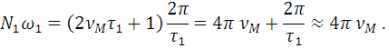
В результате функция  , дискретизированная согласно (11), принимает в данном предельном случае вид: , дискретизированная согласно (11), принимает в данном предельном случае вид:
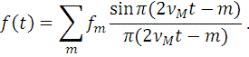 (23) (23)
Легко доказать, что разложение (23) принимает значение   во всех точках дискретизации. Рассмотрим, например точку с номером во всех точках дискретизации. Рассмотрим, например точку с номером 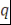 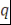 : :
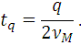
Слагаемое 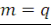 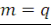 в сумме (23) дает вклад в сумме (23) дает вклад 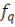 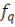 , тогда как все остальные слагаемые обращаются в ноль: , тогда как все остальные слагаемые обращаются в ноль:

Сумма (23) не дает точных нулевых значений 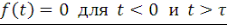 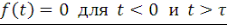 , но получаемая функция быстро обращается в ноль на обеих границах, имея малые осцилляции частоты , но получаемая функция быстро обращается в ноль на обеих границах, имея малые осцилляции частоты   . Такой тип представления функции и рассматривался Шенноном. . Такой тип представления функции и рассматривался Шенноном.
|
 Скачать 4.8 Mb.
Скачать 4.8 Mb.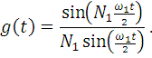 (20)
(20) 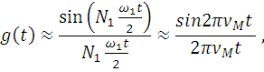 (22)
(22) 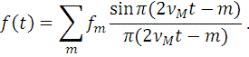 (23)
(23) 