|
|
Реферат -Тема Дискретизация и частотное разрешение. Реферат - Дискретизация и частотное разрешение. Реферат Дискретизация и частотное разрешение
Функция   , доопределенная с помощью условий (3), имеет только , доопределенная с помощью условий (3), имеет только   степеней свободы, как это следует из метода дискретизации. Если эта функция анализируется с помощью метода Фурье, то мы вместо рядов приходим к интегралам Фурье. Число членов в Фурье-анализе становится бесконечным, но они снова содержат только степеней свободы, как это следует из метода дискретизации. Если эта функция анализируется с помощью метода Фурье, то мы вместо рядов приходим к интегралам Фурье. Число членов в Фурье-анализе становится бесконечным, но они снова содержат только   независимых переменных независимых переменных   . Этот результат можно проверить, поскольку используемая функция . Этот результат можно проверить, поскольку используемая функция  идентична рассмотренному выше колоколообразному импульсу (26) и имеет спектр: идентична рассмотренному выше колоколообразному импульсу (26) и имеет спектр:
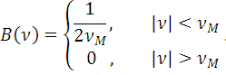 (24) (24)
следовательно
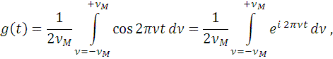 (25) (25)
и
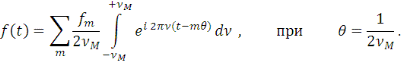 (26) (26)
Следует отметить, что главные принципы метода дискретизации были разработаны независимо рядом ученых.
5. Частотное разрешение сигналов. Приложение к анализу рентгеновских спектров поглощения атома в соединении
В разделе 2 установлен результат, согласно которому заданная функция времени f (t), существующая на интервале длительности τ, удовлетворяющая условиям f (t) =0 при t<0, t>τ, и имеющая спектр, ограниченный максимальной частотой ωmax, определяется числом независимых параметров или степеней свободы (Nidp), которое, (если не ограничиваться большими τ) находится с помощью выражения:
 (27) (27)
Как мы видели, такой результат следует из представления функции f (t) в виде ряда или интеграла Фурье, а также является следствием применения метода дискретизации сигнала, когда f (t) представляется в виде дискретизированной функции f (tm), задаваемой в точках tm с m=1,2,…,Nidp.
При этом шаг дискретизации δt в шкале t составляет δt = τ/Nidp, а частотное разрешение δω в шкале ω, характеризующее число различаемых частот в спектре, определяется выражением:
 (28) (28)
Следует отметить, что число точек дискретизации функции f (t), и как следствие, значения δt и δω, определяются величиной Nidp, а не общим числом экспериментальных точек N, в которых выполнено измерение f (t) поскольку, несмотря на независимый характер всех N измерений, они не являются независимыми для сигналов ограниченных по времени и частоте.
Применительно к теории рентгеновских спектров поглощения (X-rayabsorptionspectra или XAS) представленные результаты могут быть переписаны путем замены переменных: длительность сигнала τ → Δk = (kmax - kmin) - протяженность XAS сигнала в прямом или k-пространстве (kmin,kmax - соответственно нижняя и верхняя границы сигнала), и частота ω → 2R - частота в пространстве межатомных расстояний. В результате такой замены соотношение (27) принимает вид:
 (29) (29)
В представленном соотношении можно выделить величину разрешения δR межатомных расстояний, определяемую в соответствии с (28) как δR=Rmax/Nidp, и записать для нее выражение:
 (30) (30)
При проведении структурных исследований с помощью протяженной области рентгеновских спектров поглощения (ExtendedAbsorptionFineStructure или EXAFS), протяженность сигнала χ (k) в шкале k составляет Δk 10-15 Å-1, что в соответствии с (29) дает величину Nidp
10. При столь большом числе независимых параметров Nidp изучаемого сигнала χ (k) вторым слагаемым (
1/Nidp) в (30) можно пренебречь, после чего (30) приобретает вид:
δR = π / (2 Δk) (31)
Полученное оценочное соотношение устанавливает широко распространенный в теории EXAFS предел разрешения двух межатомных расстояний, согласно которому два расстояния R1 иR2 от поглощающего центра до атомов окружения, разность которых удовлетворяет неравенству ΔR = |R2 - R1| <δR = π/ (2Δk), не могут быть разрешены с помощью Фурье-анализа сигнала χ (k) по имеющемуся интервалу волновых чиселΔk. Оценки с помощью формулы (31) дают для предела разрешения двух межатомных расстояний величину
0.15 Å, если Δk
10 Å-1. При использовании ограниченных по протяженности интервалов Δk (
3, 4 Å-1), соответствующих околопороговой области спектра, определяемое из (29) число независимых параметров сигнала χ (k) оказывается небольшим Nidp
4, и для оценки δR воспользуемся (30), что дает величину
0.4 Å.
Представленные оценки предела разрешения двух межатомных расстояний с помощью (31) для EXAFS области спектра или с помощью (30) для околопороговой области, приближенно соответствуют критерию, при котором имеет место "визуальное” разрешение Фурье-пиков, обусловленных расстояниями R1 иR2. Такое разрешение иллюстрируется на рисунке 1, где показаны результаты Фурье-преобразования по интервалам a) Δk = 10.0 Å-1 и б) Δk = 3.0 Å-1 теоретической функции χ (k) вида:
χ (k) = {N1 sin (2kR1) + N2 sin (2kR2) } exp ( - 2σ2k2) (32)
В выражении (32): N1 - амплитуда первого слагаемого, рассчитываемого с использованием величины R1 = 2.0 Å; N2 - амплитуда второго слагаемого, которое рассчитывается с величиной R2 = 2.15 Å (обеспечивающей ΔR =│R2 - R1│= 0.15 Å) для Фурье-анализа по интервалу Δk = 10.0 Å-1, и с величиной R2 = 2.4 Å (обеспечивающей ΔR = 0.4 Å) для Фурье-анализа по интервалу Δk = 3.0 Å-1. Фактор exp (-2σ2k2) включен для приближения формы сигнала к используемой в теории XAS и соответствует учету теплового движения атомов в гармоническом приближении с характерной для металлов при комнатной температуре величиной параметра Дебая-Валлера (ДВ) σ2 = 0.005 Å2. Такой модельный сигнал (32) может быть использован для установления адекватности применения к ним критериев типа (30), (31), имеющих достаточно общий характер.

Рисунок 1. Модули Фурье-образов F (R) функций χ (k), рассчитанных по формуле (32) для ΔR = 0.15 Å - (a) и ΔR = 0.4 Å - (b). Фурье-преобразование χ (k) в случае (a) выполнено по интервалу Δk = 10.0 Å-1, а в случае (b) - по Δk = 3.0 Å-1.
Соотношения (30), (31) носят оценочный характер, поскольку в отличие от используемых при их выводе общих положений метода дискретизации и Фурье-анализа, формулируемых для сигналов произвольной формы и удовлетворяющих граничным условиям, а также условиям A или B доопределения функции в разделе 2.1, плохо соответствующим XAS сигналу. На практике предел разрешении двух межатомных расстояний с помощью Фурье-преобразования функции χ (k) по рассмотренным интервалам Δk во многих случаях оказывается гораздо выше оценок, получаемых по формулам (30), (31). Причиной этого может также служить конечность ширины Фурье-пика, соответствующего каждому из расстояний Ri, вследствие чего на ширине результирующего Фурье-пика, отвечающего двум расстояниям R1 и R2, может укладываться более одного δR-интервала (минимум две различаемые частоты). В этом случае, несмотря на отсутствие "визуального" разделения Фурье-пиков, обусловленных R1 и R2, решение задачи определения близких межатомных расстояний может быть получено путем численного сопоставления, при одинаковых Δk-интервалах, ширины и асимметрии Фурье-пика координирующих атомов в экспериментальной функции χ (k) с соответствующими характеристиками Фурье-пика пробной функции, моделирующей распределение атомов относительно поглощающего центра.
Литература
1. Боккуцци, Д. Обработка сигналов для беспроводной связи / Д. Боккуцци; Пер. с англ. Ю.Л. Цвирко; Под ред.В.И. Борисова. - М.: Техносфера, 2012. - 672 c.
. Воробьев, С.Н. Цифровая обработка сигналов: Учебник для студентов учреждений высшего профессионального образования / С.Н. Воробьев. - М.: ИЦ Академия, 2013. - 320 c.
. Лайонс, Р. Цифровая обработка сигналов: Пер. с англ. / Р. Лайонс. - М.: Бином-Пресс, 2013. - 656 c.
. Оппенгейм, А. Цифровая обработка сигналов / А. Оппенгейм, Р. Шафер; Пер. с англ. С.А. Кулешов; Пер. с англ. С.Ф. Боев. - М.: Техносфера, 2012. - 1048 c.
. Солонина, А.И. Цифровая обработка сигналов и MATLAB: Учебное пособие / А.И. Солонина, Д.М. Клионский, Т.В. Меркучева. - СПб.: БХВ-Петербург, 2013. - 512 c.
. Хименко, В.И. Статистическая акустооптика и обработка сигналов / В.И. Хименко, Д.В. Тигин. - СПб.: СПбГУ, 2012. - 292 c.
. Чан, Т.Т. Высокоскоростная цифровая обработка сигналов и проектирование аналоговых систем / Т.Т. Чан; Пер. с англ. К.В. Юдинцев. - М.: Техносфера, 2013. - 192 c. |
|
|
 Скачать 4.8 Mb.
Скачать 4.8 Mb.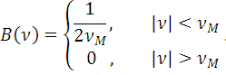 (24)
(24) 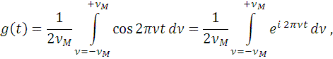 (25)
(25) 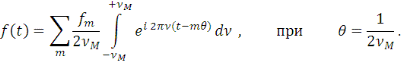 (26)
(26)  (29)
(29) (30)
(30)
