Понятие об энтропии. Понятие об энтропии Сазонов. Реферат Исполнитель студент группы Би23 Сазонов Н. Н. Гомель 2020 Понятие энтропии
 Скачать 80.08 Kb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ Учреждение образования «Гомельский государственный университет имени Франциска Скорины» Понятие об энтропии Реферат Исполнитель студент группы Би-23 Сазонов Н.Н. Гомель 2020 Понятие энтропии. Статистический смысл понятия энтропии. Вероятностное толкование понятия энтропии было дано в статистической физике Людвигом Больцманом. Введем для начала понятие термодинамической вероятности (W). Термодинамическая вероятность означает число возможных неотличимых микроскопических состояний системы реализующих определенное макроскопическое состояние этой системы. Б 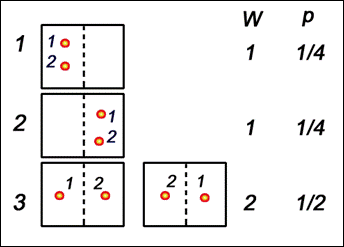 удем рассматривать простую систему всего из двух неотличимых молекул, которые находятся в некотором объеме. Мысленно разделим этот объем на две части, и, пронумеровав молекулы, найдем число способов, которым можно разместить их в этих двух частях. Рисунок 1. Мы можем увидеть, что всего 4 способа, но два нижних неотличимы, так как молекулы 1 и 2 совершенно одинаковы, и соответствуют одному и тому же макроскопическому состоянию системы. Таким образом, мы имеем три различных макроскопических состояния системы, два из которых (верхних) , реализуемых только одним способом, а третье, нижнее двумя. Число способов-термодинамическая вероятность W. Все четыре способа равновероятны, поэтому большую часть времени система будет находиться в третьем состоянии. Мы рассматривали только 2 молекулы. Число способов размещения n молекул в двух частях объема равно 2n, а число способов размещения всех молекул в одной половине объема равно 1. Энтропия термодинамического состояния системы определяется через термодинамическую вероятность: S = k·lnW, где k – постоянная Больцмана. Данное выражение называется принципом Больцмана [2]. В статистической термодинамике энтропия так же характеризует меру беспорядка и хаоса. Энтропия как мера степени неопределенности. Существование неопределённости связано с участием вероятностей в осуществлении событий. Устранение неопределённости есть увеличение вероятности наступления того, что задано как цель. Поэтому вероятности должны участвовать в математической формулировке величины устранённой неопределённости. Первая удачная попытка реализовать определение информации на такой основе осуществлена в 1928 г. Л. Хартли. Пусть возможно в данных условиях n вариантов некоторого результата. Целью является один из них. Хартли предложил характеризовать неопределённость логарифмом числа n [1]. Количественная мера s полученной информации (устранённой неопределённости)выражается логарифмом отношения вероятностей: 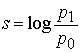 Есть один недостаток-это определение справедливо только в приближении равновероятности всех исходов. Это выполняется далеко не всегда. В пределе в этом определении невероятному исходу приравнивается неизбежный. В 1948 г. это исправил К. Шеннон. В качестве меры априорной неопределенности системы (или прерывной случайной величины  ) в теории информации применяется специальная характеристика, называемая энтропией. Понятие об энтропии является в теории информации основным.Энтропией системы называется сумма произведений вероятностей различных состояний системы на логарифмы этих вероятностей, взятая с обратным знаком: 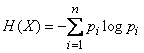 . (18.2.2)Энтропия 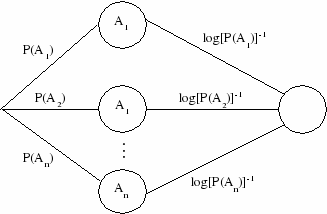 обладает рядом свойств, которые оправдывают выбор данного понятия в качестве характеристики степени неопределенности. Во-первых, обращение энтропии в нуль объясняется достоверностью состояния системы при других-невозможных. Во-вторых, энтропия о бращается в максимум при равновероятности состояний, а при увеличении числа состояний - увеличивается. Главное: свойство аддитивности.Энтропию дискретного опыта удобно находить как вес следующего графа:  Рисунок 2. Реальная ценность понятия энтропии определяется в первую очередь тем, что выражаемая им «степень неопределенности» опытов оказывается во многих случаях именно той характеристикой, которая играет роль в разнообразных процессах, встречающихся в природе, обществе и технике и так или иначе связанных с передачей и хранением каких-либо сообщений.  Понятие об информации. Понятие информации (informatio - разъяснение, осведомление, изложение) – это основное понятие не только в информатике (в информологии - области знаний, изучающей проявление информации, её представление, измерение и т.д.),но и в математике, в физике и др., плохо формализуется и структурируется. Из-за его объёмности, расплывчатости оно часто понимается неточно и неполно не только обучаемыми. Формы информации. Информация может существовать в пассивной (не актуализированной) и активной (актуализированной) форме. Информация по отношению к окружающей среде (или к использующей ее среде) бывает трех типов: входная, выходная и внутренняя. Информация по отношению к конечному результату проблемы бывает: исходная (на начало актуализации этой информации); промежуточная (от начала до завершения актуализации информации); результирующая (после завершения её актуализации). Информация по изменчивости при её актуализации бывает: постоянная (не изменяемая никогда при её актуализации); переменная (изменяемая при актуализации); смешанная - условно - постоянная (или условно-переменная). Негативное влияние информации. Информация может оказаться и вредной, влияющей негативно на сознание, например,воспитывающей восприятие мира от безразличного или же некритического - до негативного, "обозлённого", неадекватного. Информационный поток -достаточно сильный раздражитель. Пример. Негативной информацией - раздражителем может быть информация о крахе коммерческого банка, о резком росте (спаде) валютного курса, об изменении налоговой политики и др. [5]. Измерение информации. Мера Р. Хартли. Пусть имеется N состояний системы S или N опытов с различными, равновозможными, последовательными состояниями системы. Наименьшее число, при котором это возможно, называется мерой разнообразия множества состояний системы и задается формулой Р. Хартли: H=klogаN, где k - коэффициент пропорциональности (масштабирования, в зависимости от выбранной единицы измерения меры), а - основание системы меры. Если измерение ведется в экспоненциальной системе, то k=1, H=lnN (нат); если измерение было произведено в двоичной системе, то k=1/ln2, H=log2N (бит); если измерение было произведено в десятичной системе, то k=1/ln10, H=lgN (дит). Пример. Чтобы узнать положение точки в системе из двух клеток т.е. получить некоторую информацию, необходимо задать 1 вопрос: ("Левая или правая клетка?"). Узнав положение точки, мы увеличиваем суммарную информацию о системе на 1 бит (I=log22). Для системы из четырех клеток необходимо задать 2 аналогичных вопроса, а информация равна 2 битам (I=log24). Если же система имеет n различных состояний, то максимальное количество информации будет определяться по формуле: I=log2n. Справедливо утверждение Хартли: если в некотором множестве X={x1, x2, ..., xn} необходимо выделить произвольный элемент xi X, то для того, чтобы выделить (найти) его, необходимо получить не менее logan (единиц) информации [4]. Мера К. Шеннона. Шеннон вывел это определение энтропии из следующих предположений: мера должна быть непрерывной; т. е. изменение значения величины вероятности на малую величину должно вызывать малое результирующее изменение энтропии. Шеннон показал, что любое определение энтропии, удовлетворяющее этим предположениям, должно быть в форме: 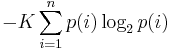 где K — константа (и в действительности нужна только для выбора единиц измерения) [3]. Шеннон определил, что измерение энтропии (H = − p1 log2 p1 − … − pn log2 pn), применяемое к источнику информации, может определить требования к минимальной пропускной способности канала, требуемой для надежной передачи информации в виде закодированных двоичных чисел. Термодинамическая мера. Информационно-термодинамический подход связывает величину энтропии системы с недостатком информации о внутренней структуре системы (не восполняемым принципиально, а не просто нерегистрируемым). При этом число состояний определяет, по существу, степень неполноты наших сведений о системе. Поставим некоторый вопрос о состоянии термодинамической системы. Пример. Предположим, что имеется термодинамическая система - газ в объеме V , который расширяется до объема 2V.  Рисунок 3. Газ объема V (a) расширяемый до 2V (б) На  с интересует вопрос о координате молекулы m газа. В начале (а) мы знали ответ на вопрос и поэтому p1=1 (lnp1=0). Изменение (убыль) информации о состоянии системы будет равно ΔI = -k ln(2V /V) = -k ln 2 (нат). Мы получили известное в термодинамике выражение для прироста энтропии в расчете на одну молекулу, и оно подтверждает второе начало термодинамики. Энтропия - мера недостатка информации о микросостоянии статической системы. Термодинамическая мера (энтропия) применима к системам, находящимся в тепловом равновесии. Для систем, далеких от теплового равновесия, например, живых биологических систем, мера-энтропия - менее подходящая [6]. Энергоинформационная (квантово-механическая) мера. Энергия (ресурс) и информация(структура) - две фундаментальные характеристики систем реального мира,связывающие их вещественные, пространственные, временные характеристики. Сейчас актуально говорить о биоэнергоинформационных мерах, отражающих механизм взаимосвязей биофизикоинформационных и вещественно-энергетических процессов в системе, в ноосфере [7]. Теорема Шеннона о кодировании при наличии помех. Теорема Шеннона — Хартли в теории информации — применение теоремы кодирования канала с шумом к архетипичному случаю непрерывного временно́го аналогового канала коммуникаций, искажённого гауссовским шумом. Теорема устанавливает шенноновскую ёмкость канала, верхнюю границу максимального количества безошибочных цифровых данных (то есть, информации), которое может быть передано по такой связи коммуникации с указанной полосой пропускания в присутствии шумового вмешательства, согласно предположению, что мощность сигнала ограничена, и гауссовский шум характеризуется известной мощностью или мощностью спектральной плотности. Закон назван в честь Клода Шеннона и Ральфа Хартли. Определение количества переданной информации при двоичном кодировании сводится к простому подсчету числа импульсов (единиц) и пауз (нулей). Таблица 1.
В случае использования неравномерного кодирования или сигналов разной длительности(ситуации (2), (3) и (4)) для отделения кода одного знака от другого между ними необходимо передавать специальный сигнал – временной разделитель (признак конца знака) или применять такие коды, которые оказываются уникальными, т.е. несовпадающими с частями других кодов. При равномерном кодировании одинаковыми по длительности сигналами (ситуация (1)) передачи специального разделителя не требуется,поскольку отделение одного кода от другого производится по общей длительности,которая для всех кодов оказывается одинаковой (или одинаковому числу бит при хранении). 4. Пример использования энтропии в прогнозировании. 4.1. Ее значение для прогнозирования. Прогнозирование является частным видом моделирования(основа познания и управления). Нельзя отрицать, что прогнозирование играет значимую роль в управлении страной, отраслью, регионом, предприятием. Необходимо учитывать СТЗП. Приведем пример прогнозирования энтропии органических соединений при повышенной температуре. Пример: Рассчитать  окиси этилена при 400, 500 и 600 К. Энтропия  окиси этилена составляет 242,4 Дж/(мольК), значения теплоемкостей C0p,T при 400, 500 и 600 К приведены в табл. 2. Рисунок 4. Зависимость идеально-газовой энтропии окиси этилена от температуры. Решение: Вычислим энтропию окиси этилена при интересующих температурах. При этом средние величины теплоемкостей окиси этилена с 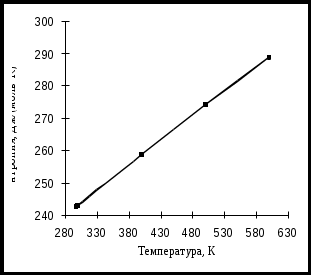 читаются величинами постоянными для каждого из температурных диапазонов (от 300 до 400, от 400 до 500 и от 500 до 600 К) по условию создания таблиц, допускающему линейную интерполяцию соседних значений в них. Результаты расчета приведены ниже и в табл. 2. сопоставлены с рекомендуемыми значениями [1].  = 242,74+(48,53+62,55)/2·(ln400 – ln300) = 258,72 Дж/(мольК); = 258,72+(62,55+75,44)/2·(ln500 – ln400) = 274,12 Дж/(мольК); = 274,12 +(75,44+86,27)/2·(ln600 – ln500) = 288,86 Дж/(мольК).Температурная зависимость  иллюстрируется рисунком 4.Таблица 2. 
Применение к рискам. Проведение классификации рисков, поставка задачи, оценивание конкретного риска, проведение структуризации риска – важные пункты при рассмотрении некоторых задач . Риски необходимо учитывать при прогнозировании экономических последствий принимаемых решений, поведения потребителей и конкурентного окружения, внешнеэкономических условий и макроэкономического развития России, экологического состояния окружающей среды, безопасности технологий, экологической опасности промышленных и иных объектов. Большое число рисков связано с природными явлениями. Риски, которые связанны с недостаточными знаниями о природе, экологических бедствиях, играют большую роль (например,неизвестен точный объем полезных ископаемых в том или ином месторождении, а потому нельзя точно предсказать развитие добывающей промышленности и объем налоговых поступлений от ее предприятий). Метод энтропии часто используют для описания неопределенностей во время компьютерного и математического. Некоторые виды неопределенностей связаны с безразличными к организации силами —природными (погодные условия) или общественными (смена правительства). Разнообразные формальные методы оценки рисков и управления ими во многих случаях (реально во всех нетривиальных ситуациях) не могут дать однозначных рекомендаций. Поэтому процедуры энтропии естественно применять не только на конечном, но и на всех остальных этапах анализа рассматриваемого организацией проекта, используя при этом весь арсенал теории и практики энтропии. . |
[1], Дж/(моль·К)