14.01 Реферат Линии и поверхности. Реферат Линии и поверхности Содержание
 Скачать 364.15 Kb. Скачать 364.15 Kb.
|
|
Реферат Линии и поверхности Содержание Введение 1 1. Понятие линии 2 2. Поверхности. Задание поверхности 6 3. Классификация поверхностей 12 Заключение 15 Список используемых источников 16 ВведениеНа протяжении многих десятилетий одной из основных дисциплин системы подготовки кадров высшей технической квалификации – инженеров механиков, инженеров строителей и других специалистов, является начертательная геометрия. Созданная 220 лет назад французским учёным Гаспаром Монжем “начертательная геометрия культивировалась в технической школе как наука, без которой немыслимо образование инженера”. Как правило, “рождение” любого изделия связано с тремя этапами: оформление и осмысливание идеи в сознании инженера, создание и обработка документации, изготовление на основе этой документации непосредственно самого изделия. Очевидно, что эти этапы не только тесно взаимосвязаны, но и не исчерпывают все нюансы подготовки и обеспечения производства готового изделия. Если изделие представляет собой какую-то конструкцию, в реальности трёхмерную, то второй этап обязательно включает представление информации об этой конструкции в виде удобном для её обработки. В настоящее время это трёхмерная компьютерная модель, необходимые расчёты и чертёж. Чертёж, по словам Монжа, есть язык техники, а грамматикой этого языка является начертательная геометрия. Линии занимают особое положение в начертательной геометрии. Используя линии, можно создать наглядные модели многих процессов и проследить их течение во времени. Линии позволяют установить и исследовать функциональную зависимость между различными величинами. С помощью линий удаётся решать многие научные и инженерные задачи, решение которых аналитическим путём часто приводит к использованию чрезвычайно громоздкого математического аппарата. Линии широко используются при конструировании поверхностей различных технических форм. 1. Понятие линииЛиния (от лат. linea — буквально льняная нить; линия, черта) — геометрическое понятие, точное и общее определение которого представляет значительные трудности и осуществляется в различных разделах геометрии по-разному. Линии занимают особое положение в начертательной геометрии. Используя линии, можно создать наглядные модели многих процессов и проследить их течение во времени. Линии позволяют установить и исследовать функциональную зависимость между различными величинами. С помощью линий удается решать многие научные и инженерные задачи, решение которых аналитическим путем часто приводит к использованию чрезвычайно громоздкого математического аппарата. Точка - это геометрическая фигура, не имеющая ни длины, ни ширины. Евклид в своей книге "Начала" определял точку как то, что не имеет частей. Отрезок – геометрическая фигура, имеющая длину, но не имеющая ширину (часть прямой, ограниченная двумя точками). Прямая - геометрическая фигура, получающаяся из отрезка неограниченным продолжением за оба его конца. Линия (латинское - льняная нить) – геометрическая фигура, получающаяся безотрывным движением карандаша по бумаге. Виды линий: Прямая Кривая Ломаная Простая Замкнутая Самопересекающаяся 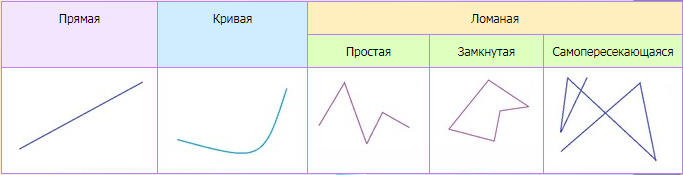 Рис. 1. Виды линий Прямая - одно из фундаментальных понятий геометрии. Считается, что она не нуждается в определении. Однако можно сказать, что это геометрическая фигура, которая получается из отрезка неограниченным продолжением его в обе стороны. Ломаная – это линия, которая составляется из отрезков так, что один из концов первого отрезка служит концом второго отрезка, другой конец второго отрезка служит концом третьего отрезка и т.д.; при этом соседние отрезки, из которых состоит ломаная, не должны составлять нового отрезка. Длина ломаной - сумма длин её сторон (звеньев) Фигура, образованная простой замкнутой ломаной и ограниченной ею внутренней областью, называется многоугольником Кривая или линия — геометрическое понятие, определяемое в разных разделах геометрии различно, иногда определяется как «длина без ширины» или как «граница фигуры». Замкнутая кривая — кривая линия, у которой начало совпадает с концом. Плоская кривая — кривая, все точки которой лежат в одной плоскости. Задание геометрических фигур в геометрии принято получать из основных (неопределяемых) понятий - точка, прямая, плоскость и расстояние, а в современном представлении также понятия множество. Базируясь на этих элементарных понятиях, линию целесообразно трактовать как траекторию перемещения точки. Такое представление линии позволяет получить определение линии, используя такие основные понятия геометрии, как точка и множество. В этом случае линию можно рассматривать как непрерывное множество всех принадлежащих ей точек. Если учесть, что положение точки при ее движении по заданной траектории будет зависеть от непрерывно меняющейся величины d (расстояние до точки от начала координат), то можно утверждать, что положение точки, принадлежащей линии, определяется непрерывно меняющейся величиной d. Тогда, окончательно приняв d за параметр, приходим к следующему определению - линия есть непрерывное однопараметрическое множество точек. В этом определении словом непрерывное подчеркивается, что двум бесконечно близким значениям параметра соответствуют две также бесконечно близкие точки. Следует иметь в виду, что данное определение линии является условным. Линии подразделяются на алгебраические, если в декартовой системе координат они определяются алгебраическими уравнениями, и трансцендентные, если они описываются трансцендентными уравнениями. Линии могут быть пространственными и плоскими. Пространственными или линиями двоякой кривизны называют линии, все точки которых не принадлежат одной плоскости. Линии, у которых все точки принадлежат одной плоскости, называют плоскими. Если алге6раическое уравнение, описывающее линию, n-й степени, то алгебраическая кривая считается n-го порядка. Порядок алгебраической кривой определяется также числом точек ее пересечения с плоскостью (для пространственной линии) или прямой (для плоской линии). При этом следует иметь в виду, что в число точек пересечения включаются точки с действительными и мнимыми координатами. Кривая линия определяется положениями составляющих ее точек. Точки кривой определяются их координатами. Кривые линии могут быть плоские, т. е. такие, которые всеми своими точками лежат в одной плоскости, и пространственные, т. е. такие, точки которых не принадлежат одной плоскости. Примерами: плоских кривых линий являются: окружность, эллипс, парабола, спираль Архимеда; примерами пространственных кривых — винтовая линия, линия пересечения боковых поверхностей прямых круговых цилиндра и конуса. Было отмечено, что пространственными кривыми называются линии, все точки которых не принадлежат одной плоскости. 2. Поверхности. Задание поверхностиПоверхности — важнейший объект окружающего нас мира. Все физические тела ограничиваются своей поверхностью. Все окружающие нас объекты можно представить в виде совокупности тех или иных поверхностей. В науке и технике, в строительстве и архитектуре — в любой отрасли поверхности играют огромную роль. Безгранично разнообразие поверхностных форм. У такого обычного слова, как поверхность, на самом деле есть множество определений. Несколько из них мы рассмотрим. Определение поверхности имеются в географии, математике, а также в других сферах деятельности. Поверхность в математике: В геометрии поверхность подразумевает одно из ключевых понятий. В школьном курсе обычно рассматриваются плоскости, а также кривые поверхности. Например, к кривой поверхности относят поверхность шара. В алгебре под поверхностью подразумевает множество точек, координаты которых имеет определенную зависимость. В высшей математике понятие поверхности тесно связано с топологией. Здесь поверхность представляет собой кусок плоскости, который может быть подвергнут деформациям. Поверхность характеризуется таким параметром, как площадь. Определить площадь поверхности того или иного объекта можно с помощью математических формул. В статье Как найти площадь поверхности куба вы можете узнать о том, как определяется площадь поверхности куба. Поверхность в географии. В географии понятие поверхности подразумевает географическую оболочку. Под этим словосочетанием понимается целостная оболочка нашей планеты, а также ее составляющие: земная кора, атмосфера, гидросфера и биосфера. Также принято включать антропосферу. Последнее понятие было введено Вернадским. Следуя его трактовке, антропосферой называют видоизмененную часть биосферы. Важно заметить, что поверхность также изучается в геоморфологии - науке, которая занимается изучение рельефа и внешним обликом планеты. Поверхность в физике и геодезии. Поверхность является важным объектом изучения в геодезии. Этот раздел топологии изучает поверхность с целью определения возможности строительства объектов. В физике понятие поверхности представляет собой границу раздела различных веществ. Например, фаза твердого и жидкого тела. Или свободы жидкости и газообразного состояния вещества. Поверхность в изобразительном искусстве. В изобразительном искусстве под поверхностью принято понимать плоскость, с которой работает художник. В качестве поверхности может выступать холст, стена, а также любая другая плоскость. Также в роли поверхности может выступать ткань, бумага или картон, металл или дерево. Принято считать, что поверхность является основой для живописи. Кроме того, поверхность может представлять собой обычный грунт. В сфере дизайна понятие поверхности аналогично. Причем работа с поверхностью подразумевает уже не только написание (создание) различных композиций, но и изменения формы поверхности, а также ее деформацию. Поверхность в начертательной геометрии. Поверхности, способы их задания и представления являются важными и интересными темами начертательной геометрии. Классификация поверхностей является предметом научных исследований и споров. Способы представления поверхностей совершенствовались на протяжении всей истории начертательной геометрии. В энциклопедическом словаре Брокгауза и Ефрона от 1898 года, начатом профессором И.Е. Андреевским и продолженном под редакцией К.К. Арсеньева и профессора Е.Е. Петрушевского, констатируется, что лучшим средством для наглядного представления поверхностей служат модели: металлическая, деревянная, гипсовая и пр. Современные средства компьютерного моделирования позволяют создать и представить поверхности любой формы — от простой до самой причудливой. В авиационной, судостроительной и автомобильной промышленности для задания корпусных поверхностей сложных форм используется плазовошаблонный метод формирования поверхности. С развитием средств компьютерного моделирования технология подготовки производства меняется. Плаз заменяется трехмерной электронной моделью изделия, выполненной в какой либо САПР, позволяющей проверить и оценить поведение модели, имитируя реальные условия эксплуатации. Во всех существующих САПР поверхности формируются по тем же принципам, что и в начертательной геометрии. Умение создавать поверхность в САПР — показатель профессионализма проектировщика, поскольку для качественного моделирования необходимо не только знание возможностей и команд той или иной системы, но и понимание формы и законов образования поверхности. В элементарной геометрии поверхность определяется как граница тела или как след движущейся линии (не вдоль себя). Толщины она не имеет. Как заключил Эвклид в своих «Началах», — «Поверхность есть то, что имеет только длину и ширину». Рассмотрим способы задания поверхностей: 1. Аналитический. Поверхность рассматривается как множество точек, координаты которых удовлетворяют уравнению типа F(x, y, z)=0, где F(x, y, z) многочлен n степени. Степень многочлена определяет порядок поверхности. Аналитический способ полезен для исследования свойств поверхностей.  Рис. 2. Гиперболоид однополостный На рис. 2 представлен гиперболоид однополостный — поверхность второго порядка, задаваемая уравнением в декартовой системе координат: 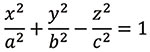 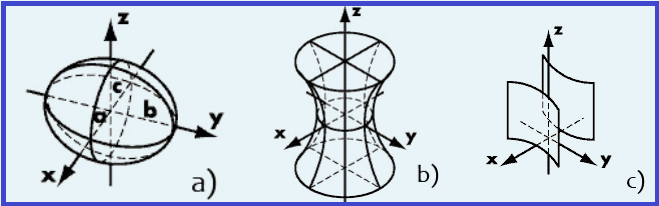 Рис. 3. Поверхности а, б, в. а – эллипсоид 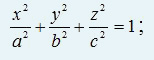 б – гиперболоид однополостный 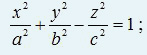 в – гиперболический цилиндр 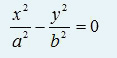 Аналитический способ задания поверхности находит широкое применение в практике, особенно если требуется исследовать свойства поверхности. 2. Задание поверхности каркасом. Каркас — это упорядоченное множество точек или линий, принадлежащих поверхности. Каркасом задают такие сложные объекты, как обшивка самолетов, корпуса автомобилей и судов. На рис. 3 изображена простейшая поверхность, заданная каркасом.  Рис. 4. Поверхность, заданная каркасом 3. Кинематический способ задания поверхности. В этом случае поверхность представляет собой множество последовательных положений заданной линии — образующей, перемещающейся в пространстве по некоторому закону (закономерные поверхности) или не подчиняющейся никакому закону (незакономерные, или случайные поверхности). В зависимости от типа образующей поверхности могут быть линейчатыми (образующая — прямая линия) и нелинейчатыми (образующая — кривая линия). Линия, вдоль которой перемещается образующая, называется направляющей. Для поверхностей, заданных кинематическим способом, вводится понятие определителя поверхности как совокупности условий, однозначно определяющих поверхность. Определитель поверхности состоит из геометрической и алгоритмической частей. Геометрическая часть определителя — геометрические фигуры, с помощью которых образуется поверхность. Алгоритмическая часть — закон образования поверхности. Линейчатые и нелинейчатые поверхности делятся на поверхности параллельного переноса, поверхности вращения и винтовые поверхности (в зависимости от движения образующей). В начертательной геометрии на комплексном чертеже поверхность может быть задана проекциями направляющих и образующих, каркасом и очерком поверхности. Поверхность считается заданной, если на комплексном чертеже можно определить все проекции точки, принадлежащей этой поверхности, по ее одной проекции. Базовые знания в области начертательной геометрии и понимание законов образования поверхностей помогают пользователю успешно реализовать задачи компьютерного моделирования. Благодаря практически неограниченным возможностям компьютерной графики в постоянно развивающихся САПР можно создавать любые поверхностные формы, точность и красота которых будет зависеть только от квалификации и мастерства проектировщика. 3. Классификация поверхностейМир поверхностей очень разнообразен. Они играют огромную роль в науке, архитектуре и технике. В математике под поверхностью подразумевается непрерывное множество точек, между координатами которых может быть установлена зависимость, определяемая уравнением типа F(x, y, z)=0, где F(x, y, z) многочлен n-й степени. Степень многочлена определяет порядок поверхности. Например, прямую линию можно назвать поверхностью первого порядка. Поверхности второго порядка – это поверхности, состоящие из плоскостей и также некоторые поверхности вращения. Любая произвольно расположенная плоскость пересекает поверхность по кривой того же порядка. Порядок поверхности также может быть определен по числу точек пересечения ее с прямой линией. В начертательной геометрии фигуры задаются графически, поэтому поверхность рассматривается как совокупность всех последовательных положений некоторой линии, перемещающейся в пространстве по определенному закону. Она называется образующей, а линия, вдоль которой она перемещается, – направляющей. Такой способ образования поверхности называется кинематическим. В начертательной геометрии классификация поверхностей производится на основании: 1. Числа порядка поверхности. 2. Формы образующих и закона образования. 3. Только закона образования. 4. Только формы образующих. Поверхности по их определенным признакам могут быть разбиты на ряд отдельных классов, причем это деление условное, так как одна и та же поверхность может быть отнесена к двум и более классам. 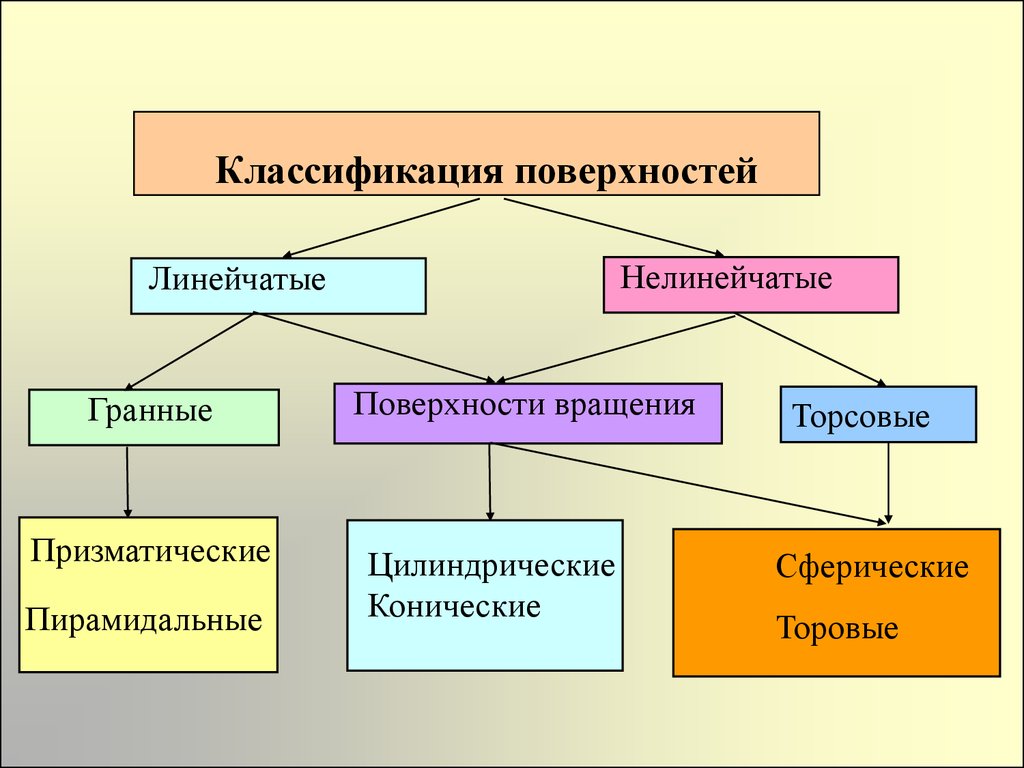 Рис. 5. Классификация поверхностей Классификация поверхностей подразделяются 1. По способу задания: Аналитические поверхности; Кинематические поверхности; скульптурные поверхности (поверхности произвольных форм). 2. По закону движения образующей: поверхности с поступательным движением образующей; поверхности с вращательным движением образующей; поверхности с винтовым движением образующей. 3. По виду образующей: поверхности с прямолинейной образующей или линейчатые поверхности; поверхности с криволинейной образующей. 4. По закону изменения формы образующей: поверхности с образующей постоянного вида; поверхности с образующей переменного вида. 5. По признаку развертывания: развертывающиеся поверхности – можно совместить с плоскостью без разрывов и складок. Сюда относятся поверхности всех многогранников, цилиндрические, конические, торсовые. неразвертывающиеся – нельзя совместить с плоскостью без разрывов и складок. Сюда относятся все остальные поверхности. Наибольшее распространение в технике получили поверхности вращения, сдвига и винтовые. Поверхности вращения – поверхности, образованные вращением произвольной образующей вокруг неподвижной оси. Направляющей поверхности вращения является окружность постоянного (цилиндр) или переменного радиуса (конус, сфера). Нормальное – перпендикулярное оси вращения сечение любой поверхности вращения, представляет собой окружность с центром на ее оси. Поверхности сдвига или так называемые поверхности экструдий – поверхности, образованные смещением произвольной образующей вдоль произвольной направляющей. Образующие и направляющие поверхности сдвига могут быть как постоянного, так и переменного вида. Винтовые поверхности – поверхности, образованные вращением произвольной образующей вокруг неподвижной оси с одновременным смещением в осевом или осевом и радиальном направлении. Направляющей винтовой поверхности является винтовая линия. ЗаключениеНа протяжении многих десятилетий одной из основных дисциплин системы подготовки кадров высшей технической квалификации – инженеров механиков, инженеров строителей и других специалистов, является начертательная геометрия. Поверхности, способы их задания и представления являются важными и интересными темами начертательной геометрии. Классификация поверхностей является предметом научных исследований и споров. Способы представления поверхностей совершенствовались на протяжении всей истории начертательной геометрии. Поверхности — важнейший объект окружающего нас мира. Все физические тела ограничиваются своей поверхностью. Все окружающие нас объекты можно представить в виде совокупности тех или иных поверхностей. В науке и технике, в строительстве и архитектуре — в любой отрасли поверхности играют огромную роль. Безгранично разнообразие поверхностных форм. В геометрии поверхность подразумевает одно из ключевых понятий. В школьном курсе обычно рассматриваются плоскости, а также кривые поверхности. Например, к кривой поверхности относят поверхность шара. В высшей математике понятие поверхности тесно связано с топологией. Здесь поверхность представляет собой кусок плоскости, который может быть подвергнут деформациям. Базовые знания в области начертательной геометрии и понимание законов образования поверхностей помогают пользователю успешно реализовать задачи компьютерного моделирования. Благодаря практически неограниченным возможностям компьютерной графики в постоянно развивающихся САПР можно создавать любые поверхностные формы, точность и красота которых будет зависеть только от квалификации и мастерства проектировщика. Список используемых источников
|
