Реферат АУЖЦП. Габидуллин И.Р. АУЖЦП РЕФЕРАТ. Реферат по дисциплине Адаптивные и оптимальные цифровые системы управления по теме Прохождение случайной функции через стационарную линейную систему

• Название: Реферат по дисциплине Адаптивные и оптимальные цифровые системы управления по теме Прохождение случайной функции через стационарную линейную систему
• Анкор: Реферат АУЖЦП
• Дата: 20.01.2023
• Размер: 371.51 Kb.
• Имя файла: Габидуллин И.Р. АУЖЦП РЕФЕРАТ.docx
• Тип: Реферат; #895847

КГЭУ	МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное бюджетное образовательное учреждение высшего образования «КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ЭНЕРГЕТИЧЕСКИЙ УНИВЕРСИТЕТ» (ФГБОУ ВО «КГЭУ»)

Кафедра АТПП


Реферат

по дисциплине «Адаптивные и оптимальные цифровые системы управления»

по теме: «Прохождение случайной функции через стационарную линейную систему»

Выполнил:

студент гр. ЗАТу-1-20

Габидуллин И.Р.

Преподаватель:
к.т.н., доцент каф. АТПП,
Борисова О.В.

Казань 2023

СОДЕРЖАНИЕ

Стр

«КАЗАНСКИЙ ГОСУДАРСТВЕННЫЙ ЭНЕРГЕТИЧЕСКИЙ УНИВЕРСИТЕТ» 1

ВВЕДЕНИЕ________________________________________________________ 3

СЛУЧАЙНЫЕ ПРОЦЕССЫ_________________________________________5

СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ__________ ___________ 11

ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА ЧЕРЕЗ ЛИНЕЙНУЮ СИСТЕМУ_______________________________________________________ 14

ЗАКЛЮЧЕНИЕ___________________________________________________24

ЛИТЕРАТУРА____________________________________________________26
ВВЕДЕНИЕ

Прежде чем рассматривать поведение автоматических систем при случайных воздействиях, напомним некоторые сведения о случайных величинах, случайных процессах и об их вероятностных характеристиках.

К категории случайных событий можно отнести такие, точное предсказание протекания которых в каждом отдельном случае оказывается невозможным.

Так, например, если бросать монету, то выпадение герба или цифры будет случайным событием. Если повторить этот эксперимент N раз, то можно зафиксировать определенное число выпадений герба  и число выпадений цифры  Относительная величина называется частотой события выпадения герба, а величина  — частотой события выпадения цифры.

Если устремить число экспериментов до бесконечности, то частоты событий будут стремиться к некоторому пределу



называемому вероятностью данного события. В рассмотренном случае очевидно, что обе вероятности выпадения герба и цифры одинаковы и равны 0,5.

Вероятность каждого события лежит в интервале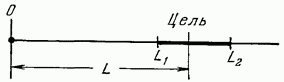 



Рис. 11.1.

Если событие является невозможным, вероятность его равна нулю; если событие является достоверным, его вероятность равна единице.

В примере с бросанием монеты рассматривалась дискретная случайная величина, которая могла принимать два фиксированных значения — выпадение герба и выпадение цифры. Существуют случайные величины, которые могут принимать непрерывные значения. Так, например, если рассмотреть стрельбу из орудия (рис. 11.1), то расстояние  от орудия до места падения снаряда будет случайной величиной, которая на определенном отрезке может принимать все возможные значения. В этом случае можно говорить о вероятности нахождения случайной величины  в некотором интервале от и до  Таблица 11.1



СЛУЧАЙНЫЕ ПРОЦЕССЫ

Случайная величина х, изменяющаяся во времени t, называется случайным или стохастическим процессом. Случайный процесс не есть определенная кривая х (t), а является множеством возможных кривых х (t), так же как случайная величина не имеет определенного значения, а является совокупностью (множеством) возможных значений.

Можно еще сказать, что случайный процесс есть такая функция времени, значение которой в каждый момент времени является случайной величиной.

Примерами случайных процессов могут, например, являться: координаты самолета, замеряемые радиолокационной станцией; угол визирования движущейся цели головкой самонаведения; помехи в системе телеуправления; нагрузка электрической сети и т. п.

Итак, в случайном процессе нет определенной зависимости х (t). Каждая кривая множества (рис. 11.11) является лишь отдельной реализацией случайного процесса. Никогда нельзя сказать заранее, по какой кривой пойдет процесс.

Однако случайный процесс может быть оценен некоторыми вероятностными характеристиками.

В каждый отдельный момент времени наблюдаются случайные величины  , каждая из которых имеет



свой закон распределения. Поскольку это — непрерывная случайная чина, то надо пользоваться понятием плотности вероятности.

Обозначим   закон распределения для всех этих отдельных случайных величин. В общем случае он меняется с течением времени. Для каждого данного t в отдельности

 будет свой закон распределения:

причем по свойству (11.14) для каждого из них

Для каждого заданного момента времени можно найти характеристики случайных величин, определенные в § 11.1. В результате будем иметь среднее по множеству (математическое ожидание)

(11.36)

и дисперсию

 (11,37)

Среднее значение случайного процесса представляет собой некоторую среднюю кривую (рис. 11.12), около которой группируются все возможные отдельные реализации этого процесса, а дисперсия D(t) или среднеквадратичное отклонение σ(t) характеризуют рассеяние отдельных возможных реализаций процесса около этой средней кривой.

Кроме этих осредненных характеристик  , которые для каждого данного момента времени являются средними по множеству, введем понятие среднего значения случайной

величины   для отдельной реализации случайного процесса х (t), которое определяется из выражения

 (11.38)

Переход к пределу здесь необходим для того, чтобы характеризовать не какой-нибудь отдельный участок кривой, а всю возможную кривую х (t) в целом.

Для того чтобы знать связь между возможными значениями случайной функции х (г) ъ последующие моменты времени со значениями в предыдущие моменты, вводится понятие двумерной плотности вероятности

,

смысл которого можно пояснить следующим образом. Вероятность того, что в момент времени t1 величина х находится в интервале  , а в момент времени t2 — в интервале  , будет  . Это есть вероятность того, что кривая х (t) пройдет вблизи двух заданных точек  . Вводится также и тг-мерная плотность вероятности

.

Если ее умножить на	, то это будет вероятность того, что кривая пройдет
вблизи заданных п точек.
Случайный процесс полностью определяется видом функций		и связью

между ними.

Простейшим типом случайного процесса является чисто случайный процесс. В таком процессе все значения случайной величины в отдельные моменты времени   не зависят друг от друга. Тогда появления значений   и т.д. будут независимыми случайными событиями, для которых вероятность их совместного наступления равна, как известно, произведению вероятностей наступления каждого из них в отдельности. Следовательно, для чисто случайного процесса

 (11.39)

и вообще

 (11.40)

Это — самые простые соотношения в теории случайных процессов. Они могут применяться для характеристики некоторых видов помех (чисто случайные хаотические помехи).

Для характеристики полезных входных сигналов систем регулирования и следящих систем соотношения (11.39) и (11.40) практически не могут применяться, так как для этих сигналов ход процесса в последующие моменты времени в какой-то степени зависит от того, что было в предыдущие моменты времени.

Так, например, если речь идет о слежении за самолетом, то он не может как угодно быстро менять свое положение и скорость. Поэтому если он в момент времени t1 занял положение х1, то этим самым его возможное положение х2 в следующий момент t2 ограничено, т. е. события   не будут независимыми. Чем более инерционен изучаемый объект, тем больше эта взаимозависимость, или корреляция. В таких случаях вместо формулы (11.39) необходимо записать

 (11.41)

 — условная вероятность того, что случайный процесс пройдет вблизи точки

, если он уже прошел через точку  . Следовательно, зная плотности вероятности ю

, можно найти также и условную плотность вероятности

 (11.42)

Кроме того, имеет место следующая связь между основными плотностями вероятности:

 (11 43)

так как   есть плотность вероятности случайной величины   безотносительно к тому, какое потом будет значение  , т. е. допускается  . Аналогичным образом любая плотность вероятности низшего порядка всегда может быть получена из высшей, т. е. высшие плотности вероятностей содержат наибольшее количество информации о случайном процессе (о взаимосвязях между возможными значениями случайной величины х в различные моменты времени).

Написанные соотношения справедливы для случайных процессов любых типов. В зависимости же от того, до какого порядка принимаются во внимание плотности вероятности, а

также от разных дополнительных гипотез о формах связи между   рассматриваются разные типы случайных процессов в отличие от чисто случайных.

Другая классификация всех случайных процессов состоит в разделении их на стационарные и нестационарные. Теория стационарных случайных процессов наиболее разработана и чаще всего применяется на практике.




СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ПРОЦЕССЫ

Стационарным случайным процессом называется такой процесс, вероятностные характеристики которого не зависят от времени. Все плотности вероятностей   не меняются при любом сдвиге рассматриваемого участка процесса во времени, т. е. при сохранении постоянной разности.

Можно сказать, что стационарный случайный процесс в какой-то мере аналогичен обычным стационарным или установившимся процессам в автоматических системах. Например, при рассмотрении обычных установившихся периодических колебаний ничего не изменится, если перенести начало отсчета на какую-нибудь величину. При этом сохранят свои значения такие характеристики, как частота, амплитуда, среднеквадратичное значение и т. п. В стационарном случайном процессе закон распределения один и тот же для каждого момента времени, т. е. плотность вероятности не зависит от времени:  .

Отсюда получаем  вдоль всего случайного процесса. Следовательно, в стационарном случайном процессе средняя линия, в отличие от общего случая (см. рис. 11.12),

будет прямая  , подобно постоянному смещению средней линии обычных периодических колебаний. Рассеяние значений переменной х в стационарном случайном

.процессе, определяемое  , также будет все время одинаковым, подобно постоянному значению среднеквадратичного отклонения обычных установившихся колебаний от средней линии.

Аналогичным образом и двумерная плотность вероятности также будет «одна и та же для одного и того же промежутка времени   между любыми t1 и t2 (рис. 11.13), т. е.

 (11.44)

и также для n-мерной плотности вероятности.

Задание всех этих функций распределения плотности определяет случайный процесс. Однако более удобно иметь дело с некоторыми осреднен-ными и характеристиками процесса.

Прежде чем перейти к ним, отметим два важных для практики ^свойства.

1.Ограничиваясь только стационарными случайными процессами, можно будет определить только установившиеся (стационарные) динамиче--ские ошибки автоматических систем при случайных воздействиях. Такой прием применялся и ранее при рассмотрении регулярных воздействий, когда определялись динамические свойства систем регулирования по величине динамических ошибок в установившемся периодическом режиме.

2.Стационарные случайные процессы обладают замечательным свойством, которое известно под названием эргодической гипотезы.

Для стационарного случайного процесса с вероятностью, равной единице (т. е. практически достоверно), всякое среднее по множеству равно соответствующему среднему по времени, в

частности   и т. д.

В самом деле, поскольку вероятностные характеристики стационарного случайного

процесса с течением времени не меняются (например,  ), то длительное наблюдение случайного процесса на одном объекте (среднее ло времени) дает в среднем такую же картину, как и большое число наблюдений, сделанное в один и тот же момент времени на большом числе одинаковых объектов (среднее по множеству).

Для многих случаев существует математическое доказательство этого свойства. Тогда оно сводится к эргодической теореме.

Итак, среднее значение (математическое ожидание) для стационарного «процесса будет

 (11.45)

Аналогичным образом могут быть записаны моменты более высоких порядков — дисперсия, среднеквадратичное отклонение и т. п.

Эргодическая гипотеза позволяет сильно упрощать все расчеты и эксперименты. Она

позволяет для определения   и т. п., вместо параллельного испытания многих однотипных систем в один и тот же момент времени, пользоваться одной кривой х (t), полученной при испытании одной системы в течение длительного времени.

Таким образом, важное свойство стационарного случайного процесса •состоит в том, что отдельная его реализация на бесконечном промежутке времени полностью определяет собой весь случайный процесс со всеми бесчисленными возможными его реализациями. Этим свойством не обладает никакой другой тип случайного процесса.

ПРОХОЖДЕНИЕ СЛУЧАЙНОГО СИГНАЛА ЧЕРЕЗ ЛИНЕЙНУЮ СИСТЕМУ

Рассмотрим линейную систему (рис. 11.25) с передаточной функцией W(р) и функцией веса  . Пусть на входе действует случайный сигнал   с корреляционной функцией

.

Выходной сигнал х2 (t) на основании формулы свертки (7.44)

Рассматривая в этой формуле математические ожидания, имеем

 (11.95)

Для получения корреляционной функции на выходе запишем исходную формулу для центрированных значений   для двух моментов времени:

 (11.96)

После перемножения получим

(11.97)

Далее, переходя к математическому ожиданию, можно найти корреляционную функцию

 (11.98)

Для определения дисперсии на выходе О2(1) в формуле (11.98) следует положить . Тогда

 (11.99)

В случае использования канонического разложения случайной функции

 (11.100)

выходная величина может быть представлена в виде

 (11.101)



где   определяется формулой (11.95), а координатные функции

 (11.102)

Корреляционная функция выходного сигнала

 (11.103)

а дисперсия

 (11.104)

Для нахождения математического ожидания   и координатных функций   в соответствии с выражениями (11.95) и (11.102) могут использоваться различные методы построения переходных процессов (см. главу 7),

В случае, когда на входе (рис. 11.25) действует случайный стационарный процесс,

корреляционная функция   зависит только от сдвига  . Однако на выходе линейной системы процесс некоторое время после включения будет устанавливаться и не будет стационарным. Корреляционная функция на выходе может быть получена из общего выражения (11.98);

 (11.105)

а дисперсия – из (11.99)

Если рассматриваемая система устойчива, то   стремятся к некоторым пределам, которые определяют стационарный процесс на выходе. Они могут быть найдены из

(11.105) и (11.1 06) , если положить  .

Тогда

Пусть, например, на входе интегрирующего звена с передаточной функцией   и функцией веса   действует белый шум с корреляционной функцией

. Тогда в соответствии: с (11.106) дисперсия на выходе будет

т. е. дисперсия растет пропорционально времени. Нетрудно видеть, что  , так как звено не является устойчивым, а оно находится на границе устойчивости (нейтральноустойчиво).

Для расчета установившегося стационарного процесса на выходе системы (рис. 11.25) более удобно исходить из известной спектральной плотности на входе  . Тогда можно легко найти спектральную плотность   выходного сигнала. Действительно, по определению спектральная плотность на входе связана с изображением Фурье   случайной величины

 соотношением (11.61):

Это же соотношение имеет место и для выходного сигнала:



В линейной системе изображения Фурье   связаны между собой посредством частотной передаточной функции:

Отсюда можно найти

 (11.109)

Таким образом, спектральная плотность выходной величины может быть получена умножением спектральной плотности входной величины на квадрат модуля частотной передаточной функции линейной системы. Отметим, что приведенное выше доказательство, вообще говоря, не является строгим, так как существование стационарного случайного процесса на выходе не доказано.

При известной спектральной, плотности   выходной величины может быть найдена корреляционная функция   по преобразованию Фурье (11.66) или (11.68).

Получим выражение (11.109) более строго. Для этого используем формулу (11.107). Так как в реальных системах весовая функция тождественно равна нулю при t < 0, то нижние пределы интегрирования можно положить равными  . Полагая, что на входе действует

центрированный процесс  , имеем

 (11.110)

Найдем теперь спектральную плотность для выходного сигнала. Она связана с корреляционной функцией соотношением (11.65):

Подставляя в последнюю формулу значение корреляционной функции из (11.110), получаем

Последнее выражение совпадает с (11.109), что и требовалось доказать, Для нахождения дисперсии, или среднего квадрата выходной величины, необходимо

проинтегрировать по всем частотам спектральную плотность:

 (11.112)

Отметим, что закон распределения для случайной величины может, вообще говоря, меняться при прохождении ее через линейную систему. Однако, в случае, если на входе линейной системы имеется нормальное распределение случайной величины х1 (t), то на выходе для случайной величины х2 (t) также будет иметь место нормальное распределение.

При вычислении интеграла (11.112) обычно приходится иметь дело с подынтегральным выражением вида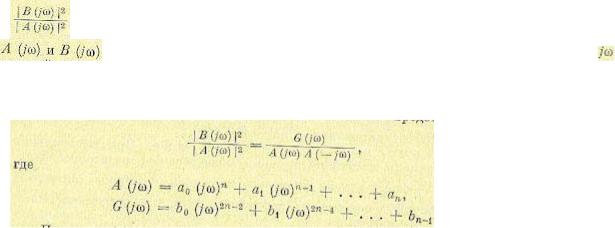

где	представляют собой некоторые полиномы от комплексной переменной .
	Наивысшую степень знаменателя обозначим 2n. Наивысшая степень числителя в реальной

системе может быть не выше 2n — 2. Для удобства интегрирования написанное выше выражение обычно представляют в виде

Полином   содержит только четные степени  . Полином   для устойчивой системы может иметь корни только в верхней полуплоскости. Область устойчивости оказалась в верхней полуплоскости вследствие того, что была использована подстановка  , а

множитель j означает поворот комплексного числа на угол  .

Таким образом, вычисление дисперсии (11.112) можно свести к нахождению интеграла

 (11.113)

В общем случае, при любом га для устойчивой системы интеграл 1п может быть представлен в виде [38]

 (11.114)

где

(11.115)

совпадает со старшим определителем Гурвица, а числитель определяется выражением

 (11.116)

Интегралы такого вида вычислены до n = 7 и сведены в таблицы (см. приложение 2). Заметим, что знаменатель правых частей приведенных в приложении 2 формул

представляет собой   — определитель Гурвица. На границе колебательной устойчивости этот определитель обращается в нуль, а дисперсия выходной величины будет стремиться к бесконечности.

В заключение рассмотрим два важных случая прохождения случайного сигнала через линейную систему.

Статистическое дифференцирование. При поступлении случайного сигнала на идеальнбе дифференцирующее устройство с передаточной функцией W (р) = р спектральная плотность выходной величины (производной от входной величины) может быть получена умножением спектральной плотности входной величины на  :

 (11.117)

при двойном дифференцировании — на   и т. д.



Статистическое интегрирование. При поступлении случайного сигнала на идеальное

интегрирующее звено с передаточной функцией  спектральная плотность выходной величины (интеграла

от входной величины) может быть получена делением интегральной плотности входной величины на  :

 (11.118)

при двойном интегрировании — на   и т. д.

ЗАКЛЮЧЕНИЕ

До сих пор поведение систем автоматического регулирования исследовалось при определенных, заданных во времени задающих и возмущающих воздействиях (ступенчатая функция, импульсная функция, гармоническое воздействие и т. д.).

Однако во многих случаях характер воздействия бывает таким, что его нельзя считать определенной функцией времени. Оно может принимать с течением времени самые разнообразные случайные значения. В таких случаях мы можем оценить только вероятность появления той или иной формы воздействия в тот или иной момент времени. Это происходит не потому, что оно неизвестно заранее, а потому, что сама природа реального задающего или возмущающего воздействия такова, что величина его в каждый момент времени и процесс его изменения с течением времени зависят от множества разнообразных величин, которые случайным образом могут комбинироваться друг с другом, появляться одновременно или с любым сдвигом во времени И т. д.

Возьмем, например, систему автоматического регулирования напряжения электрического генератора. Возмущающее воздействие здесь является результатом изменения нагрузки в сети, зависящей от включения, выключения и изменения режима работы множества потребителей электрической энергии.

Другой пример — автопилот. На него действуют обычно возмущающие воздействия случайного характера: порывы ветра и изменения других атмосферных факторов, изменение тяги, изменения напряжения питания усилителей и рулевых машинок и т. д.

Третий пример — следящие системы, на вход которых попадают вместе с полезным сигналом помехи. Например, в радиолокационной системе сопровождения отраженный от цели сигнал содержит в себе помехи в виде многочисленных флуктуаций, происходящих от вибраций и поворотов цели, замирания сигнала и т. п.

Аналогичные помехи случайной природы имеют место в других автоматических устройствах.

ЛИТЕРАТУРА

1. Бесекерский В. А., Попов Е. П. Теория систем автоматического регулирования. – СПб: Изд-во «Профессия», 2004. – 752 с.

2. Душин С.Е., Зотов Н.С., Имаев Д.Х. и др.Теория автоматического управления. Учебник/под ред. В.Б. Яковлева.-2-е изд.,перераб.-М.:Высш. шк.,2005.-567с

3. Ерофеев А.А..Теория автоматического управления. Учебник/ -2-е изд.,доп.и перераб.-СПб.:Политехника,2005.-302с.