Характеристика кинематики точки (копия). Реферат по дисциплине Гидравлика и гидромеханика нефти и газа Тема Характеристика кинематики точки студент группы 031 Альсамарраие Хушам Абдулрхман Давуд
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФГАОУ ВО «КАЗАНСКИЙ (ПРИВОЛЖСКИЙ) ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ» ИНСТИТУТ ГЕОЛОГИИ И НЕФТЕГАЗОВЫХ ТЕХНОЛОГИЙ КАФЕДРА РАЗРАБОТКИ И ЭКСПЛУАТАЦИИ МЕСТОРОЖДЕНИЙ ТРУДНОИЗВЛЕКАЕМЫХ УГЛЕВОДОРОДОВ РЕФЕРАТ По дисциплине: Гидравлика и гидромеханика нефти и газа Тема: Характеристика кинематики точки Выполнил: студент группы 03-1 Альсамарраие Хушам Абдулрхман Давуд Проверил: доцент кафедры РиЭМТУ, к.п.н, доцент Султанов Вячеслав Андреевич Казань – 2022 Содержание Список использованных источников 23 ВВЕДЕНИЕ Кинематика – раздел теоретической механики, в котором изучается движение в пространстве и во времени независимо от тех причин, которые обуславливают это движение (т.е. движение изучается с геометрической точки зрения). Таким образом, в кинематике не учитываются массы движущихся материальных тел и действующие на тела силы. Кроме научного значения кинематики, она имеет непосредственное применение в технике, в которой широко пользуются законами и формулами кинематики. Очень большое значение кинематика имеет в теории механизмов и машин. В настоящее время кинематика является хорошо исследованной областью науки. Дальнейшее развитие кинематики происходит преимущественно в виде применения ее к различным задачам техники. Движение точки по отношению к избранной системе отсчёта считается заданным, если известен способ, при помощи которого можно определить положение точки в любой момент времени. В кинематике точки рассматриваются три основных способа описания движения точки: векторный, координатный и естественный. 1 Векторный способ задания движения точки а) Положение точки в векторном способе задания движения определяется радиус-вектором 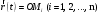 , направленным из начала координат (от тела отсчёта) к данной точке (рисунок 1). , направленным из начала координат (от тела отсчёта) к данной точке (рисунок 1). 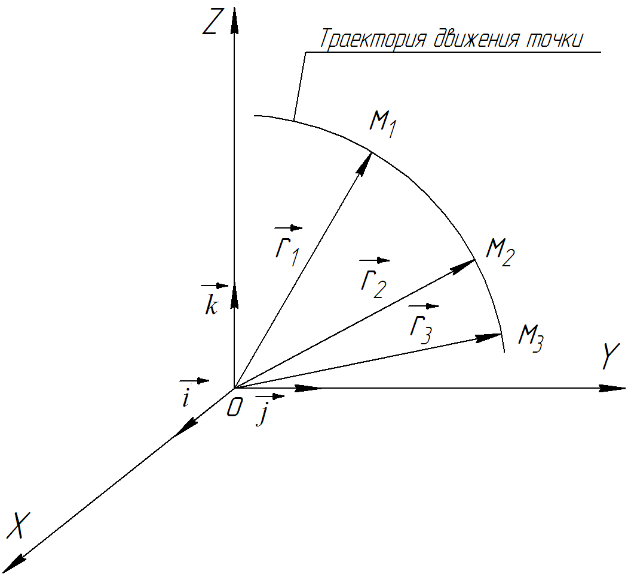 рисунок 1-Положение точки в векторном способе задания движения. Задать вектор как функцию времени – это значит уметь находить его модуль и направление в любой момент времени. При движении точки М вектор  будет с течением времени изменяться и по модулю, и по направлению. Если каждому значению скалярного аргумента t поставить в соответствие вектор будет с течением времени изменяться и по модулю, и по направлению. Если каждому значению скалярного аргумента t поставить в соответствие вектор 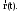 , то , то 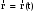 называется векторной функцией скалярного аргумента, который описывает характер движения материальной точки. Это однозначная функция, потому что точка М в каждое мгновение находится в каком-либо одном месте, она не может быть одновременно в нескольких местах. называется векторной функцией скалярного аргумента, который описывает характер движения материальной точки. Это однозначная функция, потому что точка М в каждое мгновение находится в каком-либо одном месте, она не может быть одновременно в нескольких местах.Равенство 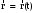 определяет собой закон движения материальной точки в векторном виде и называется векторным уравнением движения материальной точки. определяет собой закон движения материальной точки в векторном виде и называется векторным уравнением движения материальной точки.Годографом вектора называется геометрическое место концов вектора в различные моменты времени, начало которых совмещены в одной фиксированной точке, то есть годограф – это кривая. Годографом радиус – вектора является траектория (рисунок 1). Траекторией называется геометрическое место последовательных положений движущейся точки. Если в интервале времени t1 б) Пусть движущая точка находится в момент времени t1 в положении М1, определяемом радиус-вектором 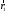 , а в момент t2 приходит в положение М2, определяемом вектором , а в момент t2 приходит в положение М2, определяемом вектором 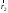 (рисунок 2). (рисунок 2).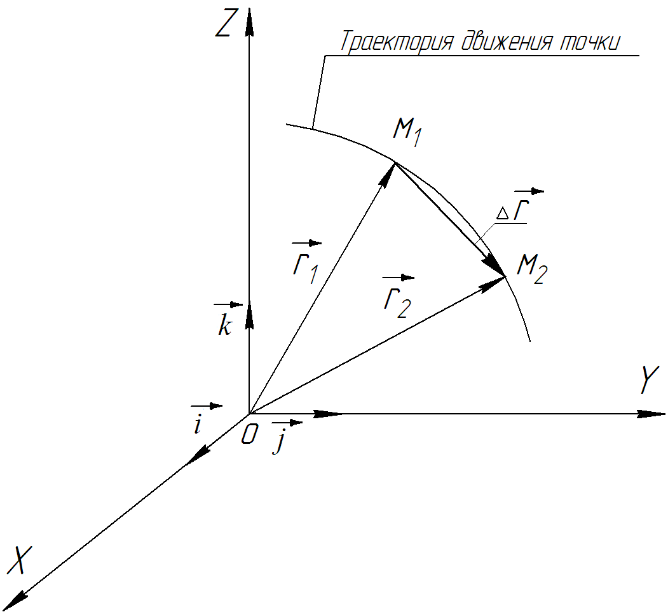 рисунок 2-движение точки в момент время. Перемещение из точки М1 в точку М2, – это вектор, направленный из одной точки, в точку конечного положения 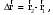 то есть перемещение - это изменение радиус-вектора (рисунок 2). то есть перемещение - это изменение радиус-вектора (рисунок 2). Вектор перемещения направлен по хорде, если точка движется по криволинейной траектории, и вдоль самой траектории, если движение точки прямолинейное. Перемещение (вектор 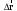 ) отмечает положение точки М только в начальное и конечное мгновения промежутка времени - ) отмечает положение точки М только в начальное и конечное мгновения промежутка времени - 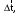 но не определяет, положение точки в каждое из мгновений этого промежутка. Чтобы это определить, необходимо время движения разбить на возможно меньшие отрезки. но не определяет, положение точки в каждое из мгновений этого промежутка. Чтобы это определить, необходимо время движения разбить на возможно меньшие отрезки.в) Одной из основных кинематических характеристик движения точки является векторная величина, называемая скоростью точки. Понятие «скорость» возникло еще в доисторическую эпоху. Сравнивая движение тел, люди усвоили тогда представление о быстроте и медленности движения. Обозначение скорости буквой  было введено Л. Эйлером. Введем сначала понятие о средней скорости точки за какой-либо промежуток времени. было введено Л. Эйлером. Введем сначала понятие о средней скорости точки за какой-либо промежуток времени. Средняя скорость – это отношение изменения радиус-вектора к тому промежутку времени, за которое оно произошло, то есть - это перемещение в единицу времени. Средняя скорость характеризует собой быстроту и направление движения точки по траектории. 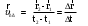 (1) (1)Вектор средней скорости 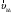 параллелен вектору перемещения параллелен вектору перемещения 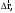 направлен в сторону движения точки, и не имеет точки приложения (Рисунок 3). 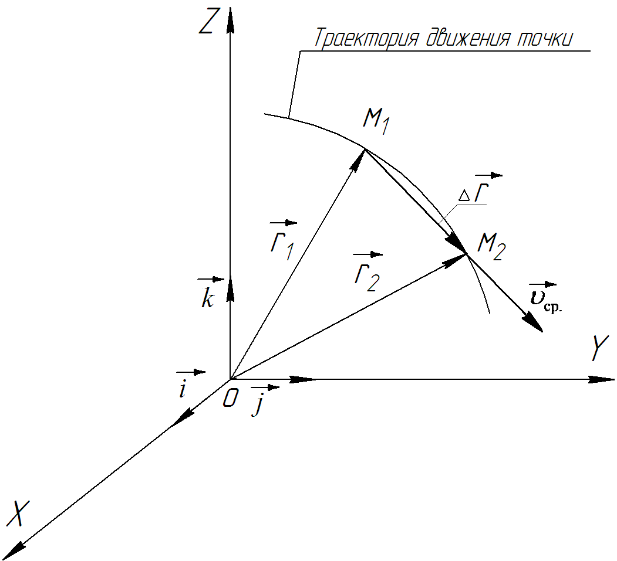 рисунок 3- Вектор средней скорости 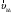 параллелен вектору перемещения параллелен вектору перемещения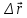 . .г) Мгновенная скорость или истинная скорость точки. Очевидно, что чем меньше будет промежуток времени, для которого вычислена средняя скорость, тем величина 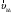 будет точнее характеризовать движение точки. Для нахождения скорости точки в фиксированный момент времени уменьшим интервал Δt до нуля и рассмотрим предел, к которому стремится средняя скорость будет точнее характеризовать движение точки. Для нахождения скорости точки в фиксированный момент времени уменьшим интервал Δt до нуля и рассмотрим предел, к которому стремится средняя скорость 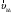 . Этот предел и будет скоростью движущийся материальной точки в данный момент (мгновенной или истинной скоростью): . Этот предел и будет скоростью движущийся материальной точки в данный момент (мгновенной или истинной скоростью): 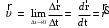 (2) (2)Производная по времени от функции обозначается точкой над символом этой функции, а вторая производная – двумя точками. Следовательно, при векторном способе задания движения точки скоростью называется первая производная радиус - вектора точки по времени. Скорость точки в этом случае характеризует быстроту изменения радиус – вектора с течением времени. д) Направление скорости При Δt→0 направление секущей М1М2 (рисунок 3) в пределе является направлением касательной. Поэтому: вектор скорости 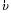 в данный момент времени направлен по касательной к годографу радиус – вектора в данной точке, т.е. по касательной к траектории точки (рисунок 4). в данный момент времени направлен по касательной к годографу радиус – вектора в данной точке, т.е. по касательной к траектории точки (рисунок 4).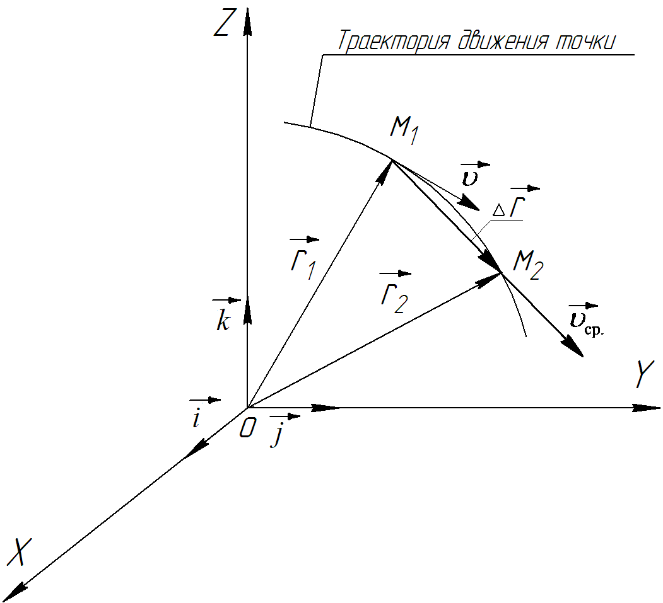 рисунок 4- прямолинейное движение точки. При прямолинейном движении точки вектор скорости 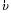 все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь по величине, а при криволинейном движении все время изменяется и направление вектора скорости точки (рисунок 5). Единица измерения скорости в системе СИ - [м/с]. все время направлен вдоль прямой, по которой движется точка, и может изменяться лишь по величине, а при криволинейном движении все время изменяется и направление вектора скорости точки (рисунок 5). Единица измерения скорости в системе СИ - [м/с]. Годограф скорости – геометрическое место концов векторов скорости движущейся точки в последовательные моменты времени, начало которых совмещены в одной фиксированной точке. 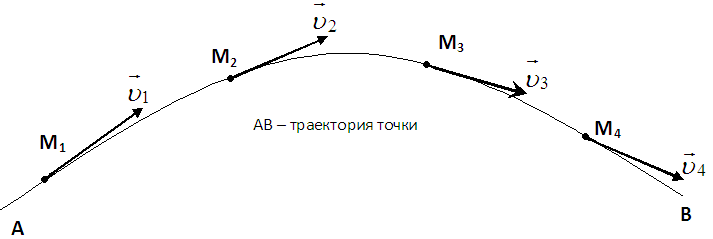 рисунок 5- векторы скорости. е) Ускорение – вторая важнейшая характеристика движущейся точки. Только при прямолинейном движении точки ее скорость сохраняет свои численное значение и направление. При неравномерном криволинейном движении скорость точки изменяется и по модулю и по направлению. Среднее ускорение точки – это отношение изменения скорости точки к тому промежутку времени, за которое оно произошло. Ускорение точки это векторная величина, которая характеризует быстроту изменения модуля и направления вектора скорости точки. 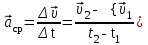 (3) (3)ё) Мгновенное ускорение или истинное ускорение точки – это предел, к которому стремится среднее ускорение при Δt→0, то есть: 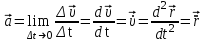 (4) (4)Ускорением называется первая производная по времени от вектора скорости 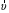 или вторая производная по времени от радиус – вектора или вторая производная по времени от радиус – вектора 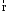 . .Размерность ускорения в системе СИ [м/с2]. ж) Направление ускорения Вектор среднего ускорения направлен по хорде (секущей) М1М2 годографа скорости (рисунок 6). 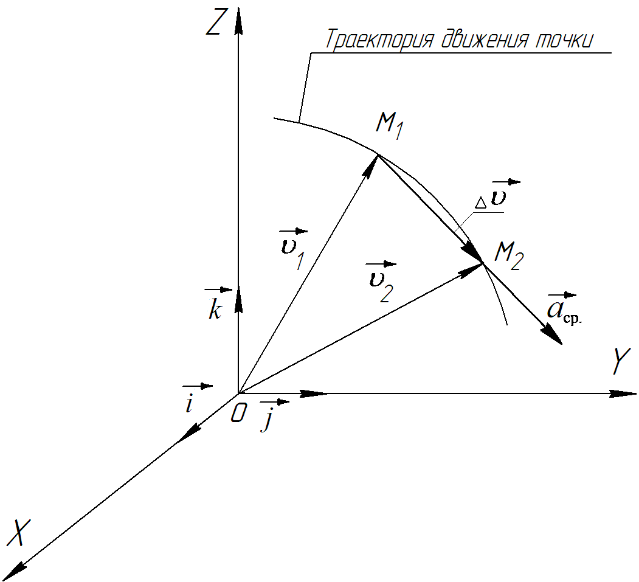 рисунок 6- Вектор среднего ускорения. При Δt→0, точка М2 стремится к точке М1 и секущая в пределе превращается в касательную к годографу скорости, то есть вектор ускорения направлен по касательной к годографу скорости в данной точке (рисунок 7). 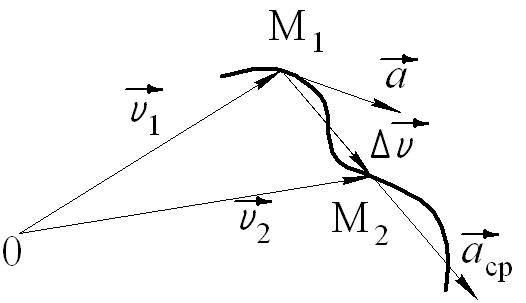 рисунок 7- прямолинейное движение точки вектор. При прямолинейном движении точки вектор ускорения 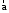 направлен вдоль прямой, по которой движется точка. направлен вдоль прямой, по которой движется точка. Векторный способ описания движения применяют, как правило, при доказательстве теорем. При решении задач используют координатный и естественный способы задания движения точки. 2 Координатный способ задания движения точки (Прямоугольные декартовы координаты) а) Положение точки Пусть OXYZ – неподвижная декартова система координат. Положение точки в системе координат OXYZ определяется тремя координатами: x, y, z (рисунок 8). 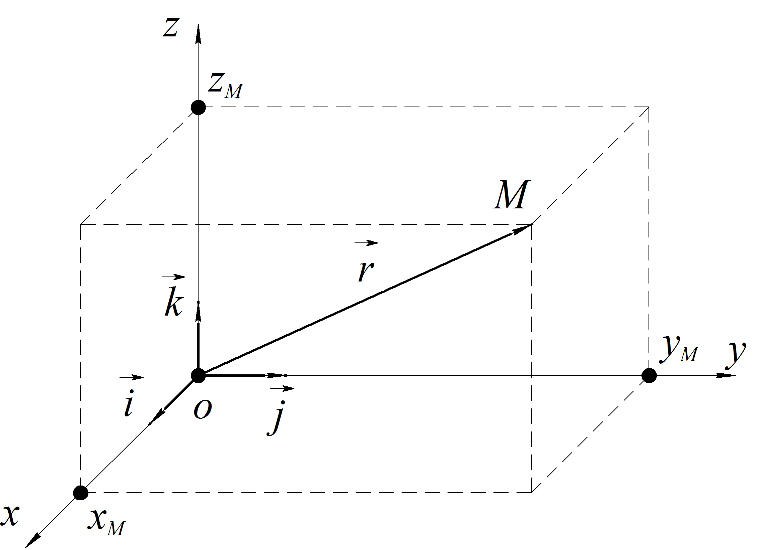 рисунок 8- система координат. При движении точки М меняются её координаты, то есть они являются функциями времени. Уравнениями движения точки в прямоугольных декартовых координатах называется зависимость координат точки от времени, которые однозначно определяют положение точки в любой момент времени, то есть задают ее движение: 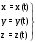 (5) (5)Если движение точки происходит все время в одной и той же плоскости, то приняв эту плоскость, например, за плоскость Оxy, получим в этом случае два уравнения движения: 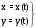 (6) (6)При прямолинейном движении точки, если вдоль ее траектории направить одну из координатных осей, (например Ох), движение точки будет определяться одним уравнением (законом прямолинейного движения точки) x = x(t) (7) При введении единичных векторов 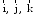 (ортов декартовой системы координат), можно записать выражение для радиус-вектора движущейся материальной точки и получить связь между векторным и координатным способами задания движения точки: (ортов декартовой системы координат), можно записать выражение для радиус-вектора движущейся материальной точки и получить связь между векторным и координатным способами задания движения точки: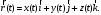 (8) (8)Уравнения движения точки являются также и уравнениями траектории точки, заданными параметрически. Для получения явного вида уравнения траектории, то есть уравнения той кривой, которая целиком или в некоторой ее части является траекторией точки, следует из уравнений движения исключить время. б) Скорость точки Определение вектора скорости при координатном способе задания движения точки сводится к нахождению проекций скорости на координатные оси x, y, z. По определению скорости: 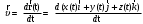 (9) (9)Это равенство продифференцируем по времени, учитывая, что единичные орты не изменяются по величине и направлениям, то есть эти векторы постоянны. Получим: 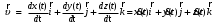 (10) (10)Отсюда находим проекции вектора скорости на оси декартовой системы координат: 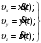 (11) (11)Проекции скорости точки на оси координат равны первым производным соответствующих координат точки по времени. Знак производных 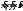 показывает направление проекций скоростей по отношению к соответствующим осям. показывает направление проекций скоростей по отношению к соответствующим осям.Алгебраическое значение вектора скорости (модуль вектора скорости) вычисляется по формуле: 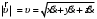 (12) (12)в) Направление скорости определяется через направляющие косинусы: 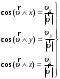 д) Ускорение Только при равномерном прямолинейном движении точки ее скорость сохраняет свое численное значение и направление. При неравномерном криволинейном движении скорость точки изменяется по модулю и направлению. Определение вектора ускорения при координатном способе задания движения точки сводится к нахождению проекций ускорения на координатные оси x, y, z. По определению: 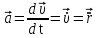 (14) (14)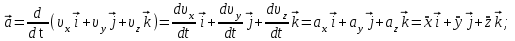 (15) (15)где: проекции ускорения на координатные оси x, y, z: 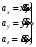 Проекции ускорения точки на оси координат равны вторым производным соответствующих координат точки по времени или первым производным по времени от проекций вектора скорости. Знак производных 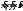 показывает направление проекций ускорений по отношению к соответствующим осям. показывает направление проекций ускорений по отношению к соответствующим осям.По известным проекциям на оси координат находим модуль ускорения: 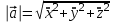 (17) (17)ё) Направление ускорения определяется через направляющие косинусы: 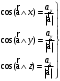 При интегрировании уравнений с помощью определенных интегралов, нижние пределы интегрирования должны соответствовать значениям интегрируемых величин в начальный момент времени, т.е. начальным условиям задачи, а верхние пределы интегрирования должны соответствовать значению интегрируемых величин при текущем времени t. 3 Естественный способ задания движения точки Естественный способ применяется, когда траектория движущейся точки известна заранее. а) Положение точки. Положение точки при естественном способе задания движения точки определяется дуговой координатой S, связанной с траекторией движения. Для того чтобы координата S определяла положение точки на траектории необходимо: - задать траекторию движения точки и закон ёе движения по ней; - выбрать начало отсчёта дуговой координаты и положительное направление отсчёта (за положительное направление отсчета, примем то направление, которое соответствует возрастанию дуговой координаты); - выбрать масштаб на траектории. 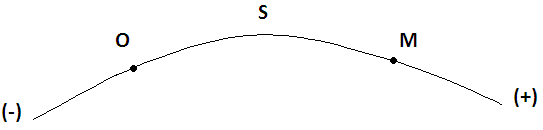 рисунок 10-положение точки. С ростом времени, Δt→0, дуговая координата изменяется так, что каждому фиксированному моменту времени t=t1 можно поставить в соответствие определенное значение дуговой координаты S = S(t), то есть, в конкретный момент времени координата “S” определяет положение точки на траектории, являясь числом. Следует иметь в виду, что дуговая координата определяет положение точки на траектории, а не пройденный ею путь. Например, если точка М начала двигаться из точки отсчета О в положительном направлении, прошла по траектории 3 м и затем вернулась в точку О, то конечное значение ее дуговой координаты равно нулю, а пройденный точкой путь составит 6 м. Функциональная зависимость S = S(t) называется законом движения материальной точки по траектории. Задание уравнения движения точки осуществляется различными способами, например, уравнениями, таблицей, в виде графика… Примером естественного способа движения является движение поезда: траектория и направление движения определены рельсами, а уравнение движения задано расписанием. в) Орты естественных координат (естественный трёхгранник) Пусть точка движется по какой-либо неплоской траектории, и, в данный момент времени, находится в точке М. Проведем в точке М к кривой соприкасающуюся плоскость, нормальную плоскость, перпендикулярную касательной, и спрямляющую плоскость, перпендикулярную соприкасающейся и нормальной плоскостям, образующую с этими плоскостями естественный трехгранник (рисунок 11). 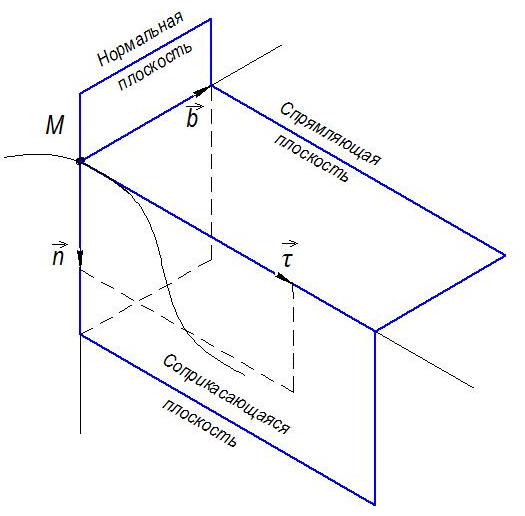 рисунок 11- неплоской траектор. Линия пересечения соприкасающейся и нормальной плоскостей называется главной нормалью кривой. Линия пересечения нормальной и спрямляющей плоскостей называется биномиальной кривой. Ортами естественных координат являются три взаимно перпендикулярных орта: главная нормаль ( 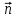 ), касательная ( ), касательная (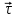 ) и бинормаль ( ) и бинормаль (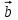 ). Эти орты образуют естественный трёхгранник, который привязан к материальной точке и движется вместе с ней, меняя свою ориентацию в пространстве, то есть орты ). Эти орты образуют естественный трёхгранник, который привязан к материальной точке и движется вместе с ней, меняя свою ориентацию в пространстве, то есть орты 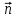 , ,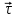 , , 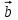 , при движении точки меняются по направлению, оставаясь неизменными по величине (рисунок 12). , при движении точки меняются по направлению, оставаясь неизменными по величине (рисунок 12).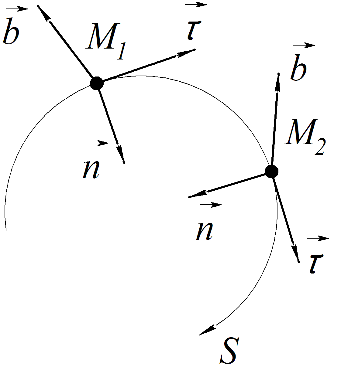 рисунок 12- Орты естественных координат. Направление: 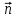 – орт главной нормали направлен в сторону вогнутости траектории (по радиусу кривизны к центру кривизны траектории к данной точке). Центр кривизны кривой в данной точке – центр окружности, наилучшим образом аппроксимирующий ход кривой в окрестности данной точки; – орт главной нормали направлен в сторону вогнутости траектории (по радиусу кривизны к центру кривизны траектории к данной точке). Центр кривизны кривой в данной точке – центр окружности, наилучшим образом аппроксимирующий ход кривой в окрестности данной точки;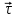 - орт касательной к траектории в данной точке, направленный в сторону возрастания дуговой координаты; - орт касательной к траектории в данной точке, направленный в сторону возрастания дуговой координаты;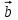 - орт бинормали перпендикулярный и нормали и касательной, направленный по отношению к касательной и главной нормали так же, как ось Оzнаправлена по отношению к осям OxиOyв правой системе координатных осей. - орт бинормали перпендикулярный и нормали и касательной, направленный по отношению к касательной и главной нормали так же, как ось Оzнаправлена по отношению к осям OxиOyв правой системе координатных осей.г) Скорость точки в естественных координатах При естественном способе задания движения точки ее дуговая координата задается как функция времени. Используем определение скорости: 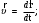 (19) (19)Преобразовав, получим: 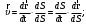 (20) (20)Из дифференциальной геометрии известно, что производная некоторого вектора по любому скалярному аргументу представляет собой вектор, направленный по касательной к годографу дифференцируемого вектора. При этом, модуль вектора 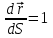 (как предел отношения длины хорды, к длине стягиваемой ею дуги). Таким образом: (как предел отношения длины хорды, к длине стягиваемой ею дуги). Таким образом: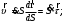 (21) (21)Проекция скорости на касательную или алгебраическая величина (модуль) скорости определяется по формуле: 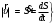 (22) (22) Единичный вектор 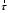 определяет направление скорости. определяет направление скорости.Так как вектор скорости 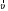 может быть направлен по касательной к траектории движущийся точки, как в сторону возрастания, так и в сторону убывания дуговой координаты S(t) в зависимости от направления движения, то проекция скорости будет либо положительной, либо отрицательной величиной (рисунок 13). может быть направлен по касательной к траектории движущийся точки, как в сторону возрастания, так и в сторону убывания дуговой координаты S(t) в зависимости от направления движения, то проекция скорости будет либо положительной, либо отрицательной величиной (рисунок 13).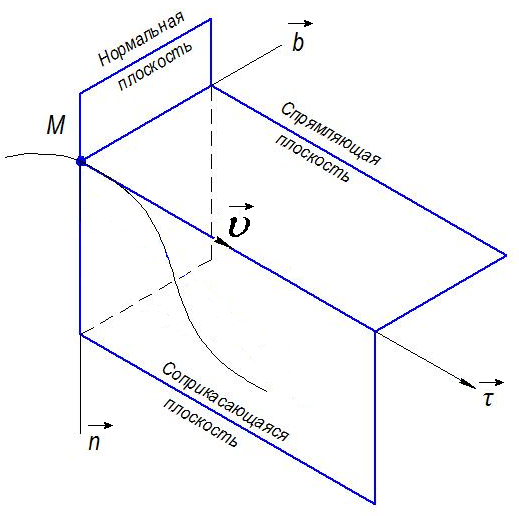 рисунок 13- вектор скорости по касательной к траектории движущийся точки. д) Ускорение в естественных координатах Определим проекции ускорения точки на оси естественных координат. Для этого найдем первую производную по времени от вектора скорости: 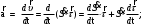 (23) (23)Преобразуем: 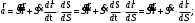 (24) (24)Вектор 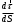 называется вектором кривизны, он равен производной от орта касательной к кривой по дуговой координате: называется вектором кривизны, он равен производной от орта касательной к кривой по дуговой координате: К= 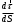 (25) (25)На различных участках кривой кривизна различна. Единственная кривая, для которой кривизна везде одинакова – это окружность, не считая прямой, для которой кривизна всегда равна нулю. Радиусом кривизны кривой  в точке называют величину, обратную кривизне кривой в этой точке. в точке называют величину, обратную кривизне кривой в этой точке. Вектор кривизны связан с единичным вектором нормали к кривой 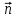 , следующим соотношением: , следующим соотношением: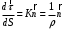 (26) (26)Таким образом, проекции ускорения на оси естественного трехгранника: 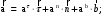 (27) (27)где: 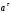 = = 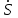 = =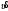 (28) (28)- проекция ускорения точки на касательную (касательная или тангенциальная составляющая ускорения точки), которая равна второй производной от дуговой координаты точки по времени или первой производной от алгебраической величины скорости точки по времени. Эта проекция имеет знак плюс, если направления касательного ускорения точки 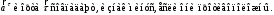 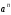 = = 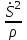 = =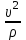 (29) (29)- проекция ускорения точки на главную нормаль (нормальная или центростремительная составляющая ускорения точки), которая равна квадрату модуля скорости точки, деленному на радиус кривизны траектории в соответствующей точке. Эта проекция всегда положительна. ав = 0 – биномиальная составляющая ускорения точки, модуль которой равен нулю. Таким образом, ускорение точки при естественном способе задания ее движения определяется по формуле: 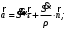 (30) (30)Тот факт, что модуль ускорения бинормали равен нулю, говорит о том, что вектор ускорения полностью лежит в плоскости траектории, то есть в соприкасающейся плоскости. Так как орт нормали перпендикулярен орту касательной, то векторы нормального и касательного ускорений взаимно перпендикулярны ( 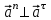 ) и от их значений зависит характер движения (рисунок 14). ) и от их значений зависит характер движения (рисунок 14). 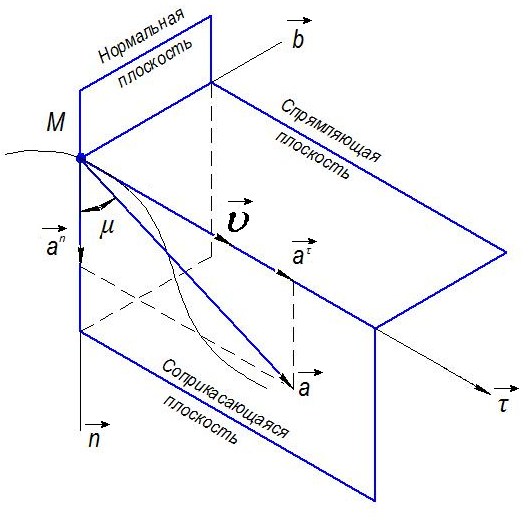 рисунок 14- Модуль ускорения бинормали. Вектор касательного ускорения 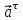 - направлен по линии скорости, по касательной к траектории, значит, изменяет скорость по величине, и, если - направлен по линии скорости, по касательной к траектории, значит, изменяет скорость по величине, и, если 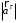 =0, то величина скорости постоянна, т.е. движение является равномерным. =0, то величина скорости постоянна, т.е. движение является равномерным.Вектор нормального ускорения 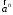 - направлен перпендикулярно скорости, ( - направлен перпендикулярно скорости, (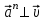 ), поэтому, нормальное ускорение изменяет скорость по направлению. Если нормальное ускорение равно нулю, то направление вектора скорости ), поэтому, нормальное ускорение изменяет скорость по направлению. Если нормальное ускорение равно нулю, то направление вектора скорости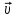 не изменяется, т.е. движение прямолинейное. не изменяется, т.е. движение прямолинейное.Вектор ускорения точки изображается диагональю параллелограмма, построенного на составляющих 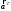 и и 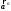 . .Учитывая ортогональность векторов нормального и касательного ускорений, то модуль вектора ускорения и угол его отклонения от нормали определяется формулами: 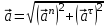 (31) (31)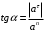 (32) (32)е) Связь координатного и естественного способа задания движения точки. Если движение точки задано координатным способом, то для перехода к естественному способу задания необходимо определить уравнение траектории, положение точки в начальный момент времени, направление движения, уравнение движения точки по ее траектории. Элемент дуги связан с координатами следующим соотношением: 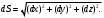 (33) (33)Интегрируя это уравнение, получим уравнение движения точки: 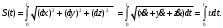 (34) (34)где: 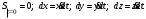 Скорость при естественном способе задания тогда будет определяться по формуле: 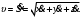 (35) (35)Для касательной составляющей ускорения получим: 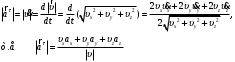 (36) (36)Как видно, Если движение точки задано координатным способом, то для перехода к естественному способу задания необходимо определить уравнение траектории, положение точки в начальный момент времени, направление движения, уравнение движения точки по ее траектории. Заключение Роль и место теоретической механики в инженерном образовании определяется тем, что она является научной базой очень многих областей современной техники. Усвоение теоретической механики усложняется тем, что в этой науке существенную роль играет моделирование и математическое представление исследуемых явлений природы. Поэтому при решении инженерных задач студенты зачастую испытывают значительные трудности. Проблему формирования у студентов исследовательского подхода к поставленным задачам (из раздела «Кинематика» курса теоретической механики) позволяет решить предлагаемое учебное пособие. В пособии доступно освещены основные темы раздела «Кинематика» с приведением всех необходимых доказательств. Даны методические рекомендации к решению задач и приведены примеры их решения. Освоению и закреплению изложенного материала помогут задания для самостоятельной работы, приведенные в конце глав пособия. Список использованных источников 1. Султанов, В.А. Теоретическая механика. Теория механизмов и машин: учебно-методическое пособие / А.Г. Мудров, В.А. Султанов, Р.Л. Сахапов. – Казань: Изд-во Казан. ун-та, 2018. – 48 с.; 2. Новожилов, А. И. Краткий курс теоретической механики: учеб. пособие / А. И. Новожилов; под ред. В. Н. Филимонова. – 2-е изд., перераб. и доп.; Владим. гос. ун-т. – Владимир: Изд-во Владим. гос. ун-та, 2006. – 242 с. 3. Тарг, С.М. Краткий курс теоретической механики: учеб. для вузов/ С.М.Тарг. – 20-е изд., стер – М.: Высш. шк., 2010 – 416 с. 4. Яблонский, А.А. Курс теоретической механики: для вузов/ А.А Яблонский, В.М Никифорова – 5-е, испр. изд., М.: Высш. школа, 1977-368 с. 5. Айзенберг, Т. Б. Руководство к решению задач по теоретической механике / Т. Б. Айзенберг, И. М. Воронков, В. М. Осецкий. – Изд.6-е.– М. : Высш. шк., 1968. – 392 с 6. https://natalibrilenova.ru/teoreticheskaya-mehanika-statika (30.09.2022) 7. https://topuch.ru/sirota-dmitrij-yureevich-teoreticheskaya-mehanika-konspekt/index.html (13.10.2022) 8. https://ozlib.com/944846/tehnika/privedenie_sistemy_tsentru (14.10.2022) |
