Математическое моделирование. Реферат по дисциплине Компьютерное моделирование месторождений нефти
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
Кафедра «Разработка и эксплуатация нефтяных и газовых месторождений» Реферат по дисциплине «Компьютерное моделирование месторождений нефти» Вариант № 14
Самара, 2021г. Содержание Введение………………...……………………………………………………3 Граничные условия…………………………………………………….…....4 Список литературы ………………………………………………………..21 Введение В данной работе понятия, будут распространены на различные задачи моделирования пластов, в которых рассматривается фильтрация одного флюида в пространстве двух измерений. Здесь представлены некоторые новые задачи и методы, используемые только для расчетов двумерной (2-D) фильтрации. эти методы будут использованы при решении многофазных задач и трехмерных задач. Хотя было уже рассмотрено много методов решения практических задач моделирования пластов, однако они применялись только для крайне идеализированного одномерного пространства. В этой главе будут рассмотрены детали некоторых практических моделей газовых месторождений и нефтяных месторождений с давлением выше давления насыщения. Здесь также будут представлены численные методы решения дифференциальных уравнений в частных производных, описывающих двумерную фильтрацию. Некоторые методы, которые могут быть применены для матричных уравнений, полученных в результате конечно-разностной аппроксимации дифференциальных уравнений в частных производных. 1.1 ГРАНИЧНЫЕ УСЛОВИЯ Для моделирования необходимо знать начальное состояние пласта (начальные условия) и взаимодействие пласта с его окружением. Во многих важных случаях мы не представляем в деталях этих условий, и для получения разумных оценок требуется хорошее инженерное понимание ситуации. Граничные условия Должны задаваться на скважинах и на внешней границе пласта. Граничные условия могут быть трех типов: 1— на границе задан расход; 2 — течение на границе отсутствует и 3—на границе задано давление. За исключением односкважинных систем в цилиндрических координатах, скважины моделируют с помощью точечных или линейных источников, определяемых функцией Дирака. Данный подход необходим вследствие малости радиуса скважины в сравнении с размерами блока при исследованиях на площадной и профильной моделях. В данном разделе рассмотрим случаи, когда задан нулевой или некоторый конечный расход через границу. Мы также покажем, что граничные условия «с расходом» и «без расхода» могут быть реализованы одинаково заменой действительных граничных условий однородными граничными условиями Неймана (отсутствие потока) и введением потока в систему или из нее через источники или стоки. На рис. 1.1 и 1.2 показаны типичные граничные условия для площадной и односкважинной моделей. Рассмотрим теперь детально границы «с расходом» и «без расхода». 1.1.1. Границы «без расхода» (непроницаемые границы) Когда нет течения через границу (Г2 на рис. 1.1 и 1.2), компонента вектора скорости, нормальная к граничной поверхности, должна быть нулевой. Соответствующую компоненту получим, взяв скалярное произведение вектора скорости фильтрации на вектор нормали n. На границе Г2. 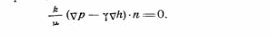 (1.1) (1.1)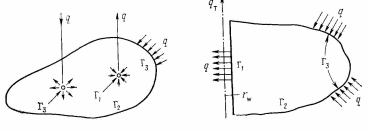 Рис 1.1 Граница в площадных системах Рис. 1.2. Границы в односкважинных системах При моделировании пластов границы обычно аппроксимируются границами блоков, параллельными одному из координатных направлений. Таким образом, в площадных (x,y) моделях для всех границ, нормальных направлению оси x,(1.2), а для всех границ, нормальных направлению оси y(1.3). 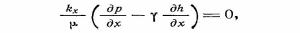 (1.2) (1.2)(1.3) 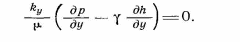 1.1.2. Границы « расходом» Если задан некоторый расход через границ (Г1 или Г3 на рис. 1.1 и 1.2), нормальная компонента вектора скорости н границе должна равняться этом расходу: 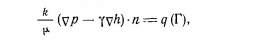 (1.4) (1.4)А общий поток через границу получают интегрированием q в уравнении (1.4) по границе. Например, н границ Г3 (см. рис. 1.2) общий расход 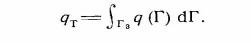 (1.5) (1.5)Если реальная граница охватывает более одного блока и если задан общий расход qТ, то он должен быт соответствующим образом распределен по всем граничным блокам. Эта проблема будет обсуждаться в следующем разделе, где рассматриваются конечноразностное или дискретно представление граничных условий. 1.1.3 Дискретизация граничных условий Для примера рассмотри точк3 (i, k) н вертикальной границе сетки в профильной модели (рис. 1.3). Если расход через границу нулевой,dp/dx=0 можно аппроксимировать с использованием выражения второго порядка точности. 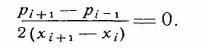 (1.6) (1.6)В данном случае предполагается полная симметрия свойств по хi, а сам метод известен как «метод отражения». Здесь сохраняются симметрия и порядок аппроксимации конечно-разностных уравнений. 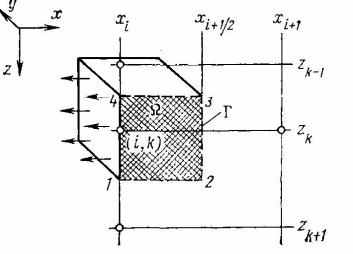 Рис. 1.3 Типичный граничный блок сетки в профильной модели Поток в систему или из нее можно учитывать двумя различными способами. В первом случае предполагается, что граница блока (1—4) изолирована, а в разностное уравнение вводится член источника (стока) соответствующей интенсивности, в другом, что источник (сток) нулевой, а градиент давления на границе блока dp/dxi, имеет значение, при котором через границу протекает нужное количество флюида. Как показано ниже, эти, вроде бы два различных, подхода оказываются идентичными на конечно-разностном уровне. Рассмотрим следующую упрощенную форму уравнения (1.4) 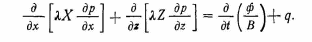 (1.7) (1.7)Применим к данному уравнению интегральный метод получения разностных аппроксимаций. В результате интегрирования по объему блока (i,k) получим 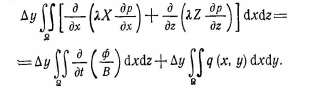 (1.8) (1.8)Левая часть этого уравнения может быть с помощью теоремы Грина (см., например, Морсе и Фешбах, 1953, с. 34 и 803) преобразована в контурный интеграл 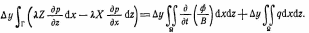 (1.9) (1.9)Контурный интеграл по Г можно разделить на четыре части по четырем сторонам поперечного сечения блока в плоскости х, z. Предположим, что производные dp/dz и dp/dx постоянны на каждой из этих сторон и могут быть аппроксимированы конечными разностями. Тогда получим следующие аппроксимации: ( 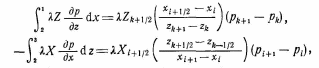 1.10) 1.10)(1.11) 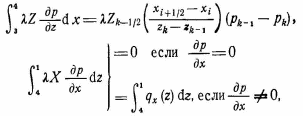 (1.12) (1.12)(1.13a) (1.13b) где Δ yqx(z) — расход на единицу длины границы (1—4) блока (i,k): 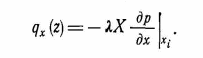 (1.14) Если расход учитывается с помощью уравнения (1.13b), последний член в уравнении (1.9) должен быть равен нулю, а общий расход через границу из уравнения (1.13) можно записать как 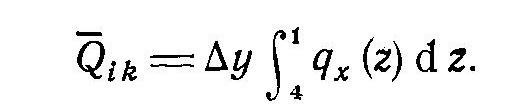 (1.15) (1.15)Однако, если используется уравнение (1.13а), общий расход из блока 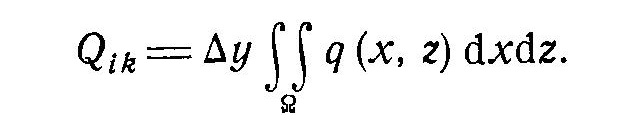 (1.16) Эти два уравнения по-разному интерпретируют особые граничные условия «с источником». 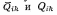 и должны быть равны, так как они представляют один и тот же суммарный отбор из блока (i, k). На конечно-разностном уровне, где q(x,z) и qx(z) в уравнениях (1.15) и (1.16) должны предполагаться постоянными в блоке, нет различия между этими двумя интерпретациями граничных условий. Это подтверждает возможность использования уравнения (1.13а) при всех способах моделирования. Первый член правой части уравнения (1.8) может быть аппроксимирован выражением и должны быть равны, так как они представляют один и тот же суммарный отбор из блока (i, k). На конечно-разностном уровне, где q(x,z) и qx(z) в уравнениях (1.15) и (1.16) должны предполагаться постоянными в блоке, нет различия между этими двумя интерпретациями граничных условий. Это подтверждает возможность использования уравнения (1.13а) при всех способах моделирования. Первый член правой части уравнения (1.8) может быть аппроксимирован выражением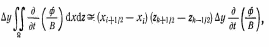 (1.17) которое идентично соответствующему члену из уравнения (1.7),умноженному ‘на фактический объем блока. Запишем стандартную конечно-разностную аппроксимацию для уравнения (1.7), 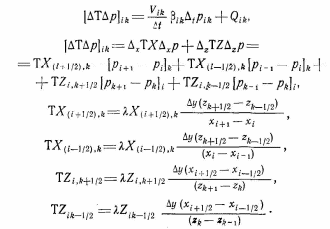 (1.18) (1.19) (1.20) (1.21) (1.22) (1.23) Эти выражения применимы к произвольному целому блоку внутри пласта. Сравнение уравнений (1.10) и (1.13) показывает, что общую форму можно использовать для граничного блока (i,k), если положить ( 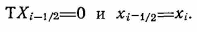 1.24) 1.24)Подобным образом можно легко получить разновидности общего выражения (1.18) для других границ. Единственная нерешенная проблема для граничных условий—задание расходов Qik для каждого блока при заданном общем расходе QT нескольких блоков в процессе моделирования профилей и для моделей о единичной скважине, вскрывающей несколько блоков. Простейшее ее решение — распределить расход в соответствии с проводимостью блока 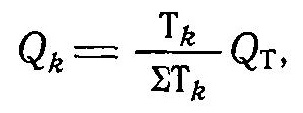 (1.25) (1.25)где Тk — определенная соответствующим образом проводимость. Список литературы 1.Азиз Х., Сеттари Э. Математическое моделирование пластовых систем./ Перевод с английского А. В. КОРОЛЕВА и В. П. КЕСТНЕРА под редакцией канд. геол.-минерал. наук М. М. МАКСИМОВА— Москва–Ижевск: Институт компьютерных исследований, 2004, 416 стр. |

