Теория Вероятности. Реферат по дисциплине теория вероятности Ручина Н. А гр 10менз Проверил Гладков В. В нижний Новгород, 2011
 Скачать 0.71 Mb.
|
  Оценка параметров генеральной совокупности Характеристики положения Основными параметрами генеральной совокупности являются математическое ожидание (генеральная средняя) М(Х) и среднее квадратическое отклонение s. Это постоянные величины, которые можно оценить по выборочным данным. Оценка генерального параметра, выражаемая одним числом, называется точечной. Точечной оценкой генеральной средней является выборочное среднее  . Выборочным средним называется среднее арифметическое значение признака выборочной совокупности. Если все значения x1, x2,..., xn признака выборки различны (или если данные не сгруппированы), то: 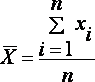 Если же все значения признака x1, x2,..., xn имеют соответственно частоты n1, n2,..., nk, причем n1 + n2 +...+ nk = n (или если выборочное среднее вычисляется по вариационному ряду), то 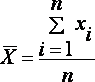В том случае, когда статистические данные представлены в виде интервального вариационного ряда, при вычислении выборочного среднего значениями вариант считают середины интервалов. Выборочное среднее является основной характеристикой положения, показывает центр распределения совокупности, позволяет охарактеризовать исследуемую совокупность одним числом, проследить тенденцию развития, сравнить различные совокупности (выборочное среднее является той точкой, сумма отклонений наблюдений от которой равна 0). Для оценки степени разброса (отклонения) какого-то показателя от его среднего значения, наряду с максимальным и минимальным значениями, используются понятия дисперсии и стандартного отклонения. Дисперсия выборки или выборочная дисперсия (от английского variance) – это мера изменчивости переменной. Термин впервые введен Фишером в 1918 году. Выборочной дисперсией Dв называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения . Если все значения x1, x2,..., xn признака выборки объема n различны, то: 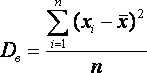 Если же все значения признака x1, x2,..., xn имеют соответственно частоты n1, n2,..., nk, причем n1 + n2 +...+ nk = n, то 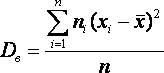 Дисперсия меняется от нуля до бесконечности. Крайнее значение 0 означает отсутствие изменчивости, когда значения переменной постоянны. Среднее квадратическое отклонение (стандартное отклонение), (от английского standard deviation) вычисляется как корень квадратный из дисперсии.  Чем выше дисперсия или стандартное отклонение, тем сильнее разбросаны значения переменной относительно среднего. Непараметрическими характеристиками положения являются мода и медиана. Модой Mo называется варианта, имеющая наибольшую частоту или относительную частоту. Медианой Me называется варианта, которая делит вариационный ряд на две части, равные по числу вариант. При нечетном числе вариант (n=2k+1) Me = xk+1, а при четном числе вариант (n=2k) Me = (xk + xk+1)/2. Методика проверки статистических гипотез Пусть задана случайная выборка  — последовательность объектов из множества Х . Предполагается, что на множестве Х существует некоторая неизвестная вероятностная мера Р . Методика состоит в следующем. Формулируется нулевая гипотеза  о распределении вероятностей на множестве Х. Гипотеза формулируется исходя из требований прикладной задачи. Чаще всего рассматриваются две гипотезы — основная или нулевая и альтернативная  . Иногда альтернатива не формулируется в явном виде; тогда предполагается, что означает «не » . Иногда рассматривается сразу несколько альтернатив. В математической статистике хорошо изучено несколько десятков «наиболее часто встречающихся» типов гипотез, и известны ещё сотни специальных вариантов и разновидностей. Примеры приводятся ниже. Задаётся некоторая статистика (функция выборки)  , для которой в условиях справедливости гипотезы выводится функция распределения и/или плотность распределения . Вопрос о том, какую статистику надо взять для проверки той или иной гипотезы, часто не имеет однозначного ответа. Есть целый ряд требований, которым должна удовлетворять «хорошая» статистика Т . Вывод функции распределения при заданных и Т является строгой математической задачей, которая решается методами теории вероятностей; в справочниках приводятся готовые формулы для ; в статистических пакетах имеются готовые вычислительные процедуры. Фиксируется уровень значимости — допустимая для данной задачи вероятность ошибки первого рода, то есть того, что гипотеза на самом деле верна, но будет отвергнута процедурой проверки. Это должно быть достаточно малое число . На практике часто полагают . На множестве допустимых значений Т статистики выделяется критическое множество  наименее вероятных значений статистики Т, такое, что  . Вычисление границ критического множества как функции от уровня значимости является строгой математической задачей, которая в большинстве практических случаев имеет готовое простое решение. Собственно статистический тест (статистический критерий) заключается в проверке условия: если  , то делается вывод «данные противоречат нулевой гипотезе при уровне значимости ». Гипотеза отвергается. если  , то делается вывод «данные не противоречат нулевой гипотезе при уровне значимости ». Гипотеза принимается. Итак, статистический критерий определяется статистикой Т и критическим множеством , которое зависит от уровня значимости . Замечание. Если данные не противоречат нулевой гипотезе, это ещё не значит, что гипотеза верна. Тому есть две причины. По мере увеличения длины выборки нулевая гипотеза может сначала приниматься, но потом выявятся более тонкие несоответствия данных гипотезе, и она будет отвергнута. То есть многое зависит от объёма данных; если данных не хватает, можно принять даже самую неправдоподобную гипотезу. Выбранная статистика Т может отражать не всю информацию, содержащуюся в гипотезе . В таком случае увеличивается вероятность ошибки второго рода — нулевая гипотеза может быть принята, хотя на самом деле она не верна. Допустим, например, что = «распределение нормально»; =  «коэффициент асимметрии»; тогда выборка с любым симметричным распределением будет признана нормальной. Чтобы избегать таких ошибок, следует пользоваться более мощными критериями. Альтернативная методика на основе достигаемого уровня значимости Широкое распространение методики фиксированного уровня значимости было вызвано сложностью вычисления многих статистических критериев в до компьютерную эпоху. |