Теория Вероятности. Реферат по дисциплине теория вероятности Ручина Н. А гр 10менз Проверил Гладков В. В нижний Новгород, 2011
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
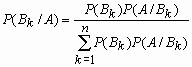 Теорема -формула Байеса. Пусть 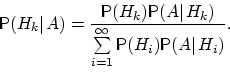 Доказательство. По определению условной вероятности, 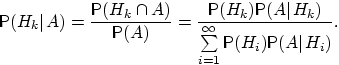 Вернёмся к примеру 21. Изделие выбирается наудачу из всей произведённой продукции. Рассмотрим три гипотезы: Пусть Убедились, что полученные нами в примере 21 вероятности совпадают с вероятностями, вычисленными по формуле полной вероятности и формуле Байеса. Два стрелка подбрасывают монетку и выбирают, кто из них стреляет по мишени (одной пулей). Первый стрелок попадает по мишени с вероятностью 1, второй стрелок — с вероятностью 0,00001. Можно сделать два предположения об эксперименте: Рассмотрим событие Поэтому вероятность пуле попасть в мишень \Предположим, что событие А произошло. Какова теперь апостериорная (a'posteriori — «после опыта») вероятность каждой из гипотез 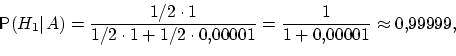 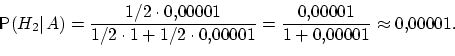 Последовательность испытаний (схема Бернулли) Схема Бернулли состоит в следующем: производится последовательность испытаний, в каждом из которых вероятность наступления определенного события А одна и та же и равна р. Испытания предполагаются независимыми (т.е. считается, что вероятность появления события А в каждом из испытаний не зависит от того, появилось или не появилось это событие в других испытаниях). Наступление события А обычно называют успехом, а ненаступление - неудачей. Обозначим вероятность неудачи q=1-P(A)=(1-p). Вероятность того, что в n независимых испытаниях успех наступит ровно m раз, выражается формулой Бернулли: Вероятность Рn(m) при данном n сначала увеличивается при увеличении m от 0 до некоторого значения m0, а затем уменьшается при изменении m от m0 до n. Поэтому m0, называют наивероятнейшим числом наступлений успеха в опытах. Это число m0, заключено между числами np-q и np+p (или, что то же самое, между числами n(p+1)-1 и n(p+1)) .Если число np-q - целое число, то наивероятнейших чисел два: np-q и np+p. Важное замечание. Если np-q< 0, то наивероятнейшее число выигрышей равно нулю. Пример. Игральная кость бросается 4 раза. При каждом броске нас интересует событие А={выпала шестерка}. Решение: Здесь четыре испытания, и т.к. кубик симметричен, то p=P(A)=1/6, q=1-p=5/6. Вероятность того, что в 4 независимых испытаниях успех наступит ровно m раз (m < 4), выражается формулой Бернулли: Посчитаем эти значения и запишем их в таблицу.  Самое вероятное число успехов в нашем случае m0=0. Пример. Вероятность появления успеха равна 3/5. Найти наивероятнейшее число наступлений успеха, если число испытаний равно 19, 20. Решение: при n =19 находим Таким образом, максимальная вероятность достигается для двух значений m0, равных 11 и 12. Эта вероятность равна P19(11)=P19(12)=0,1797. При n=20 максимальная вероятность достигается только для одного значения m0, т.к. На практике в случае, когда n велико, а p мало (обычно p < 0,1; npq < 10) вместо формулы Бернулли применяют приближенную формулу Пуассона Пример: Радиоаппаратура состоит из 1000 элементов. Вероятность отказа одного элемента в течение года равна 0,002. Какова вероятность отказа двух элементов за год? Какова вероятность отказа не менее двух элементов за год? Решение: будем рассматривать работу каждого элемента как отдельное испытание. Обозначим А={отказ элемента за год}. P(A)=p=0,002, l=np=1000*0,002=2 По формуле Пуассона Обозначим через P1000( > 2) вероятность отказа не менее двух элементов за год. Переходя к противоположному событию, вычислим P1000( > 2) как: Теорема Муавра — Лапласа - одна из предельных теорем теории вероятностей, установлена Лапласом в 1812. Если при каждом из n независимых испытаний вероятность появления некоторого случайного события Е равна р (0<р<1) и m - число испытаний, в которых Е фактически наступает, то вероятность неравенства близка (при больших n) к значению интеграла Лапласа. При рассмотрении количества m появлений события A в n испытаниях Бернулли чаще всего нужно найти вероятность того, что m заключено между некоторыми значениями a и b. Так как при достаточно больших n промежуток [a,b] содержит большое число единиц, то непосредственное использование биномиального распределения ребует громоздких вычислений, так как нужно суммировать большое число определённых по этой формуле вероятностей. Поэтому используют асимптотическое выражение для биномиального распределения при условии, что p фиксированно, а \Если в схеме Бернулли n стремится к бесконечности, p (0 < p < 1) постоянно, величина 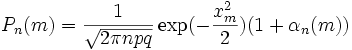 где где Приближённую формулу 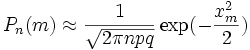 рекомендуется применять при n > 100 и npq > 20. Для доказательства Теоремы будем использовать формулу Стирлинга из математического анализа: где 0 < θs < 1 / 12s. При больших s величина θ очень мала, и приближённая формула Стирлинга, записанная в простом виде, даёт малую относительную ошибку, быстро стремящуюся к нулю, когда Нас будут интересовать значения m, не очень отличающиеся от наивероятнейшего. Тогда при фиксированном p условие Поэтому использование приближённой формулы Стирлинга для замены факториалов в биномиальном распределении допустимо, и мы получаем 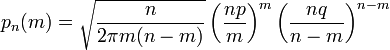 Также понадобится использование отклонения относительной частоты от наивероятнейшего значения Переписываем полученное ранее биномиальное распределение с факториалами, заменёнными по приближённой формуле Стирлинга: 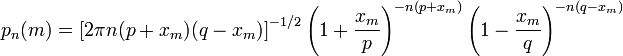 Предположим, что xm < pq (7) Взяв логарифм второго и третьего множителей равенства (6), применим разложение в ряд Тейлора: 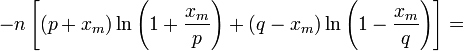 Располагаем члены этого разложения по степеням xm: 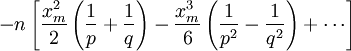 Предположим, что при Это условие, как уже было указанно выше, означает, что рассматриваются значения m, не очень далёкие от наивероятнейшего. Очевидно, что (10) обеспечивает выполнение (7) и (3). Теперь, пренебрегая вторым и последующими членами в разложении (6), получаем, что логарифм произведения второго и третьего членов произведения в правой части (8) равен Отбрасывая малые слагаемые в скобках первого множителя (6), получаем: 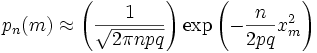 Отбрасывая малые слагаемые в скобках первого множителя (6), получаем: 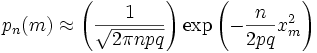 Обозначив 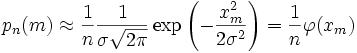 Где Поскольку в интервале [m,m + 1) имеется только одно целое число m, то можно сказать, что pn(m) есть вероятность попадания m в интервал [m,m + 1). Из (5) следует, что изменению m на 1 соответствует изменение xm на Поэтому вероятность попадания m в интервал [m,m + 1) равна вероятности попадания xm в промежуток [xm,xm + Δx) Когда Таким образом, если то для отклонения относительной частоты от наивероятнейшего значения справедлива ассимптотическая формула (16), в которой Таким образом теорема доказана. Интегральная теорема Муавра—Лапласа Пусть 0 Это означает, что для вычисления вероятности того, что число успехов в n испытаниях Бернулли заключено между k1 и k2, можно использовать формулу 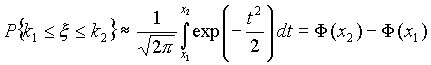 где где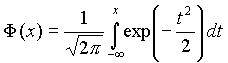 функция Лапласа, Точность этой приближенной формулы растет с ростом n., функция Лапласа, Точность этой приближенной формулы растет с ростом n., 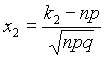 , ,ПУАССОНА ТЕОРЕМА - 1) П. т.- предельная теорема теории вероятностей, являющаяся частным случаем больших чисел закона. П. т. обобщает Бернулли теорему на случай независимых испытаний, вероятность появления в к-рых нек-рого события зависит от номера испытаний (т. н. схема Пуассона). Формулировка П. т. такова: если в последовательности независимых испытаний событие Анаступает с вероятностями pk, зависящими от номера испытания k, k=1,2, . . ., mn/n - частота Ав первых писпытаниях, то при любом e>0 вероятность неравенства 2) П. т.- предельная теорема теории вероятностей о сходимости биномиального распределения к Пуассона распределению:если Р п(m) - вероятность того, что в писпытаниях Бернулли нек-рое событие Анаступает ровно траз, причем и вероятность Ав каждом испытании равна р, то при больших значениях n и 1/р вероятность Р п (т).близка к Это неравенство указывает ошибку при замене Р n (т).величиной Последующие обобщения П. т. создавались в двух основных направлениях. С одной стороны, появились уточнения П. т., основанные на асимптотич. разложениях, с другой - были установлены общие условия сходимости сумм независимых случайных величин к распределению Пуассона. Случайные величины Определения, примеры Часто в результате испытания происходят события, заключающиеся в том, что некоторая величина принимает одно из своих возможных значений. В таких случаях удобно вместо множества событий рассматривать одну переменную величину (называемую случайной величиной). Случайная величина обозначается через X, Y, Z, … и т.д. Случайной называется величина, которая в результате испытания может принять то или иное возможное значение, неизвестное заранее, но обязательно одно. Пример. В студенческой группе 25 человек. Пусть величина Х – число студентов, находящихся в аудитории перед началом занятий. Ее возможными значениями будут числа 0, 1, 2,…,25. При каждом испытании (начало занятий) величина Х обязательно примет одно из своих возможных значений, т.е. наступит одно из событий Х = 0, Х = 1, …, Х = 25. Пример. Измерение курса акции некоторого предприятия. Возможные события заключаются в том, что стоимость акции Y примет некоторое значение в пределах от 0 до ∞. Пример. Однократное бросание игральной кости. Возможные события заключаются в том, что на верхней грани выпадает Z: 1, 2, 3, 4, 5, 6. Пример. Подбрасывается монета n раз. Возможные результаты: герб выпал 0, 1, 2, …, n раз. Различают дискретные и непрерывные случайные величины. Если множество возможных значений случайной величины конечно или образуют бесконечную числовую последовательность, то такая случайная величина называется дискретной (примеры 3.1, 3.3, 3.4). Случайная величина, множество значений которой заполняет сплошь некоторый числовой промежуток, называется непрерывной (пример 3.2). Заметим, что дискретные и непрерывные величины не исчерпывают все типы случайных величин. Если случайная величина не относится ни к дискретным, ни к непрерывным случайным величинам, то ее называют смешанной. Очевидно, что для полной характеристики дискретной случайной величины мало знать ее значения. Необходимо им поставить в соответствие вероятности. Соответствие между всеми возможными значениями дискретной случайной величины и их вероятностями называется законом распределения данной случайной величины. Простейшая формой задания закона распределения дискретной случайной величины является таблица, в которой перечислены возможные значения случайной величины (обычно в порядке возрастания) и соответствующие им вероятности:
акая таблица называется рядом распределения. Допустим, что число возможных значений случайной величины конечно: х1, х2, …, хn. При одном испытании случайная величина принимает одно и только одно постоянное значение. Поэтому события Х = хi (i = 1, 2, … , n) образуют полную группу попарно независимых событий. Следовательно, р1 + р2 + … + рn = 1. Можно закон распределения изобразить и графически, откладывая на оси абсцисс возможные значения случайной величины, а на оси ординат – соответствующие вероятности. Для большей выразительности полученные точки соединяются прямолинейными отрезками. Получающая при этом фигура называется многоугольником (полигоном) распределения. Функция распределения вероятностей Непрерывную случайную величину нельзя охарактеризовать перечнем всех возможных ее значений и их вероятностей. Естественно, встает вопрос о том, нельзя ли охарактеризовать случайную величину иным способом, одинаково годным как для дискретных, так и для непрерывных случайных величин. Функцией распределения случайной величины Х называют функцию F(x), определяющую для каждого значения х, вероятность того, что случайная величина Х примет значение меньше х, т.е. F(x) = P (X Иногда функцию F(x) называют интегральной функцией распределения. Функция распределения обладает следующими свойствами: 1. Значение функции распределения принадлежит отрезку [0,1]: 0 ≤ F(x) ≤ 1. 2. Функции распределения есть неубывающая функция. 3. Вероятность того, что случайная величина Х примет значение, заключенное в интервале (а, b), равна приращению функции распределения на этом интервале: Р(а < X < b) = F(b) – F(а). (2.1) 4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то F(x) = 0 при х ≤ а; F(x) = 1 при х ≥ b. 5. Справедливы следующие предельные отношения: |
