Теория Вероятности. Реферат по дисциплине теория вероятности Ручина Н. А гр 10менз Проверил Гладков В. В нижний Новгород, 2011

• Название: Реферат по дисциплине теория вероятности Ручина Н. А гр 10менз Проверил Гладков В. В нижний Новгород, 2011
• Анкор: Теория Вероятности.doc
• Дата: 21.12.2017
• Размер: 0.71 Mb.
• Имя файла: Теория Вероятности.doc
• Тип: Реферат; #12380
• страница: 4 из 6

.

Для дискретной случайной величины Х, которая может принимать значения х1, х2, …,хn, функция распределения имеет вид

где неравенство под знаком суммы означает, что суммирование касается всех тех значений хi, величина которых меньше х.

Поясним эту формулу исходя из определения функции F(x). Предположим, что аргумент х принял какое-то определенное, но такое, что выполняется неравенство xi

Предположим теперь, что для непрерывной случайной величины Х ее функция распределения F(x) имеет непрерывную производную

F'(x)= φ(x).

Функцию φ(x) называют плотностью вероятности (для данного распределения) или дифференциальной функцией.

Так как плотность вероятности φ(x) является производной неубывающей функции F(x), то она неотрицательна: φ(x)≥0. В отличие от функции распределения, плотность вероятности может принимать сколь угодно большие значения.

Так как F(x) является первообразной для φ(x), то на основании формулы Ньютона-Лейбница имеем . Отсюда в силу P(a ≤ X ≤ b) = (3.1)

P(a ≤ X ≤ b) = . (2.3)

Полагая а=–∞ и b=+∞, получаем достоверное событие Х принадлежащее (–∞, +∞), вероятность которого равна единице. Следовательно,

В частности, если все возможные значения случайной величины принадлежат интервалу (а, b), то . Полагая в формуле а = –∞, b = х и обозначая для ясности переменную интегрирования t, получим функцию распределения

F(x) = P(– ∞ < X < x) = .

Задача 2.1. Найти интегральную функцию распределения случайной величины Х, заданной рядом распределения:

Х	1	2	3
Р	0,3	0,2	0,5

остроить ее график.

Решение. Пусть х ≤ 1, тогда F(x) = 0, так как событие Х < х будет невозможным. Если 1 < х ≤ 2, то на основании равенства (3.2) имеем F(x) = p1 = 0,3. Если 2 < х ≤ 3, то F(x) = p1 + p2 = 0,5.

Если х > 3, то F(x) = p1 + p2 + p3 = 1. Окончательно получаем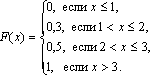



График функции F(х) изображен на рис.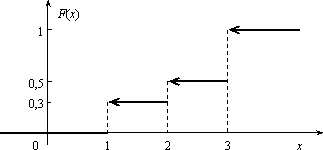


Задача. Функция распределения случайной величины Х задана выражением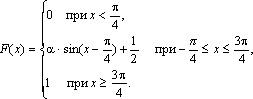



Найти коэффициент α; вероятность попадания значения случайной величины Х в результате опыта в интервал (π/4; 3π/4); построить график функции.

Решение . При х=3 π/4 функция F(x ) равна 1, т.е. α∙ sin (3π/4–π/4)+1/2=1, или α∙si n(π/2) + 1/2 = 1. Откуда α = 1/2.

Подставляя а = π/4 и b = 3π/4 в равенство (3.1), получаем

π (π/4
График функции у =1/2∙sin(х-π/4 )+1/2 отличается от графика функции у = sinх тем, что он «сжат» по оси Оу в два раза, сдвинут вправо на π/4, поднят вверх на 1/2. Воспользовавшись этим замечанием, отразим график F(x)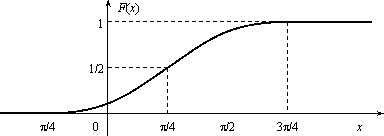


Числовые характеристики случайной величины

Функция распределения содержит полную информацию о случайной величине. На практике функцию распределения не всегда можно установить; иногда такого исчерпывающего знания и не требуется. Частичную информацию о случайной величине дают числовые характеристики, которые в зависимости от рода информации делятся на следующие группы.

1. Характеристики положения случайной величины на числовой оси (мода Мo, медиана Мe, математическое ожидание М(Х)).

2. Характеристики разброса случайной величины около среднего значения (дисперсия D(X), среднее квадратическое отклонение σ(х)).

3. Характеристики формы кривой y = φ(x) (асимметрия As, эксцесс Ех).

Рассмотрим подробнее каждую из указанных характеристик. Математическое ожидание случайной величины Х указывает некоторое среднее значение, около которого группируются все возможные значения Х. Для дискретной случайной величины, которая может принимать лишь конечное число возможных значений, математическим ожиданием называют сумму произведений всех возможных значений случайной величины на вероятность этих значений: .

Математическое ожидание случайной величины Х указывает некоторое среднее значение, около которого группируются все возможные значения Х. Для дискретной случайной величины, которая может принимать лишь конечное число возможных значений, математическим ожиданием называют сумму произведений всех возможных значений случайной величины на вероятность этих значений:

Для непрерывной случайной величины Х, имеющей заданную плотность распределения φ(x) математическим ожиданием называется следующий интеграл:

Здесь предполагается, что несобственный интеграл сходится абсолютно, т.е. существует.

Свойства математического ожидания:

1. М(С) = C, где С = const;

2. M(C∙Х) = С∙М(Х);

3. М(Х ± Y) = М(Х) ± М(Y), где X и Y – любые случайные величины;

4. М(Х∙Y)=М(Х)∙М(Y), где X и Y – независимые случайные величины.

Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина.

Модой дискретной случайной величины, обозначаемой Мо, называется ее наиболее вероятное значение (рис. 2.3), а модой непрерывной случайной величины – значение, при котором плотность вероятности максимальна (рис. 2.4).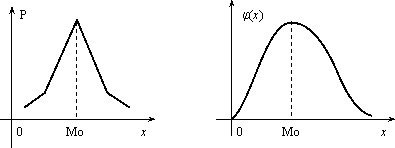



Рис. 2.3 Рис. 2.4

Медианой непрерывной случайной величины Х называется такое ее значение Ме, для которого одинаково вероятно, окажется ли случайная величина меньше или больше Ме, т.е.

Р(Х < Ме) = Р(X > Ме)

Из определения медианы следует, что Р(Х<Ме) = 0,5, т.е. F (Ме) = 0,5. Геометрически медиану можно истолковывать как абсциссу, в которой ордината φ(x) делит пополам площадь, ограниченную кривой распределения (рис. 2.5). В случае симметричного распределения медиана совпадает с модой и математическим ожиданием (рис. 2.6).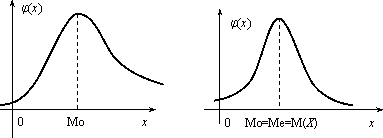



Рис. 2.5 Рис. 2.6

Дисперсией случайной величины называется математическое ожидание квадрата ее отклонения от математического ожидания

D(X) = M(X –М(Х))2.

Дисперсию случайной величины Х удобно вычислять по формуле:

а) для дискретной величины

; (2.6)

б) для непрерывной случайной величины

j(х)dx – [M(X)]2 . (2.7)

Дисперсия обладает следующими свойствами:

1. D(C) = 0, где С = const;

2. D(C×X) = C2∙D(X);

3. D(X±Y) = D(X) + D(Y), если X и Y независимые случайные величины.

Средним квадратическим отклонением случайной величины Х называется арифметический корень из дисперсии, т.е.

σ(X) =.

Заметим, что размерность σ(х) совпадает с размерностью самой случайной величины Х, поэтому среднее квадратическое отклонение более удобно для характеристики рассеяния.

Обобщением основных числовых характеристик случайных величин является понятие моментов случайной величины.

Центральным моментом k-го порядка μk случайной величины Х называется математическое ожидание величины (Х–М(Х))k, т.е. μk = М(Х–М(Х))k.

Центральный момент второго порядка – это дисперсия случайной величины.

Для дискретной случайной величины начальный момент выражается суммой αk = , а центральный – суммой μk = где рi = p(X = xi). Для начального и центрального моментов непрерывной случайной величины можно получить следующие равенства:

αk = ,  μk = ,

где φ(x) – плотность распределения случайной величины Х.

Величина As = μ3 / σ3 называется коэффициентом асимметрии.

Если коэффициент асимметрии отрицательный, то это говорит о большом влиянии на величину m3 отрицательных отклонений. В этом случае кривая распределения (рис.2.7) более полога слева от М(Х). Если коэффициент As положительный, а значит, преобладает влияние положительных отклонений, то кривая распределения (рис.2.7) более полога справа. Практически определяют знак асимметрии по расположению кривой распределения относительно моды (точки максимума дифференциальной функции).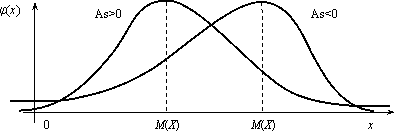



Эксцессом Еk называется величина

Еk = μ4 / σ4 – 3.

Можно показать, что для наиболее распространенного в природе нормального закона распределения, который будет рассматриваться в следующем параграфе, отношение μ4 / σ4 = 3. Поэтому эксцесс служит для сравнения данного распределения с нормальным, у которого эксцесс равен нулю. Можно было бы доказать, что распределения более островершинные, чем нормальное, имеют эксцесс Еk > 0, а более плосковершинные – имеют эксцесс Еk < 0 (рис.3.8).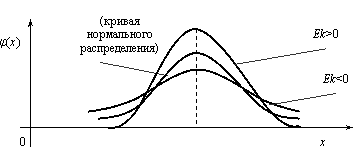



Задача. Дискретная случайная величина Х, имеющая смысл числа курьеров, задействованных для доставки корреспонденции в коммерческой организации, задана законом распределения:

Х	0	1	2	3
Р	0,4	0,1	0,3	0,2

Найти математическое ожидание, дисперсию, среднее квадратическое отклонение.

Решение. Так как случайная величина является дискретной, то для вычисления М(Х) воспользуемся формулой (3.4). Имеем

М( х) = х1 × р1 + х2 × р2 + х3 × р3 + х4 × р4 = 0 × 0,4 + 1 ×0,1 + 2 × 0,3 + 3 × 0,2 = 1,3.

Найдем дисперсию D(x). Предварительно найдем математическое ожидание от х2:

М(х2) = х12 × р1 + х22 × р2+ х32 × р3+ х42 × р4 = 02 × 0,4 + 12 × 0,1 + 22 × 0,3 + 32 × 0,2 = 3,1.

Далее по формуле (3.6) получаем

D(X) = 3,1 – 1,32 = 3,1 – 1,69 = 1,41.

Найдем среднее квадратическое отклонение. Имеем

σ(х) =.

Таким образом, среднее число курьеров равно 1,3 со средним разбросом 1,22.

Задача. Непрерывная случайная величина Х задана функцией распределения: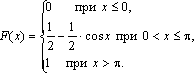

Найти математическое ожидание и дисперсию этой случайной величины. Решение . По определению дифференциальной функции φ(х) = F ¢ ( x ). Отсюда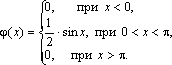

В точках х = 0 и х = π функция φ(х) не дифференцируема. По формуле (3.5) получаем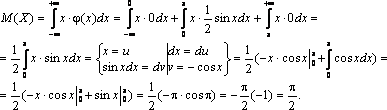


Находим сначала М(Х2). Имеем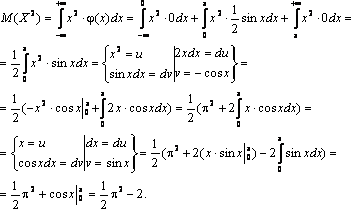



Далее по формуле (3.7) получаем .

Биномиальное распределение

Пусть в каждом из n независимых испытаний событие А может произойти с одной и той же вероятностью р (следовательно, вероятность непоявления q =1 – p). Дискретная случайная величина Х – число наступлений события А – имеет распределение, которое называется биномиальным.

Очевидно, событие А в n испытаниях может либо не появиться, либо появиться 1 раз, либо 2 раза, …, либо n раз. Таким образом, возможные значения Х таковы: х1 = 0, х2 = 1, х3 = 2,…, хn+1 = n. Вероятность возможного значения Х = k (числа k появления события) вычисляют по формуле Бернулли:

Pn(k) = Cnk·pk·qn–k,

где k = 0, 1, 2, …, n.

Ряд распределения случайной величины Х, подчиненной биномиальному закону, можно представить в виде следующей таблицы:

Х	0	1	…	k	…	n
Р	Cn0· p0·qn	Cn1 ·p1·qn–1	…	Cnk·pk·qn–k	…	Cnn·pn·q0

Название закона связано с тем, что вероятности Pn(k) при k = 0, 1, 2, …, n являются членами разложения бинома Ньютона

(p + q)n = qn + Cn1·p1·qn–1 + … + Cnk·pk·qn–k + … +pn.

Отсюда сразу видно, что сумма всех вероятностей второй строки таблицы равна 1, так как p +q =1.

Задача. В цехе работают четыре станка. Вероятность остановки в течение часа каждого из них равна 0,8. 1) Найти закон распределения случайной величины Х – числа станков, остановившихся в течение часа. 2) Найти вероятность остановки в течение часа: а) более двух станков; б) от одного до трех станков.

Решение. 1) Возможные значения Х следующие: 0, 1, 2, 3, 4. Вероятность этих значений можно найти по формуле Бернулли, потому что Х имеет биномиальное распределение (станки останавливаются независимо друг от друга с постоянной вероятностью р=0,8). Получаем р4(0)=q4=0,0016, р4(1)=C41p1q3=0,0256, р4(2)= C42 p2q2 = 0,154, р4(3)=C43 · p3· q1=0,41, р4(4)= p 4 = 0,41. Ряд распределения имеет вид

Х	0	1	2	3	4
Р	0,0016	0,0256	0,154	0,41	0,41

2) а) Р(X>2)= P(X =3)+P(X=4)=0,41+0,41=0,82.

б) P1≤X≤3)=P(X=1)+P(X=2)+ P(X=3)=0,0256+0,154+0,41=0,59.

Распределение Пуассона

Это распределение представляет собой предельный случай биномиального, когда вероятность р очень мала, а число испытаний n велико.

Таким образом, им можно пользоваться при описании частот распределения редких событий, таких, например, как случай обширных наводнений на протяжении долгого периода времени наблюдений.

Дискретная случайная величина Х, которая может принимать только целые неотрицательные значения с вероятностями ,

где k – число появления событий в n независимых испытаниях, λ = n· p (среднее число появлений события в n испытаниях), называется распределенной по закону Пуассона с параметром λ.

В отличие от биномиального распределения здесь случайная величина может принимать бесконечное множество значений, представляющее собой бесконечную последовательность целых чисел 0, 1, 2, 3, … .

Закон Пуассона описывает число событий k, происходящих за одинаковые промежутки времени. При этом полагается, что события появляются независимо друг от друга с постоянной средней интенсивностью, которая характеризуется параметром λ = n·p . Так как для распределения Пуассона вероятность р появления события в каждом испытании мала, то это распределение называют законом распределения редких явлений.

По распределению Пуассона распределено, например число посетителей магазина или банка за определенный промежуток времени, при этом λ – среднее число посетителей за это время.

Предположим, что в среднем в магазин приходит 2,1 покупатель в минуту. Тогда, используя (3.8), получаем, например, вероятности того, что магазин посетят за минуту 1, 4 и 10 посетителей: