Теория Вероятности. Реферат по дисциплине теория вероятности Ручина Н. А гр 10менз Проверил Гладков В. В нижний Новгород, 2011
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
Основанием считать статистическое распределение пуассоновским является близость значений статистических характеристик и S2 (которые являются статистическими приближениями математического ожидания и дисперсии), так как для теоретического распределения Пуассона имеет место: М(Х) = D( X) = λ. Равномерное распределение Непрерывная случайная величина Х имеет равномерное распределение на отрезке [a, b], если ее плотность имеет следующий вид: 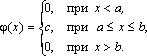 График плотности распределения показан на рис. 2.9. 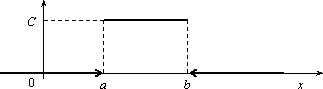 φ(х) Рис. 2.9 Найдем значение постоянной С. Так как площадь, ограниченная кривой распределения и осью Ох, равна 1, то откуда С = 1/(b – a). Пусть [ α, β ] Ì [a, b]. Тогда где L – длина (линейная мера) всего отрезка [a, b] и – длина частичного отрезка [ α, β]. Значения случайной величины Х, т.е. точки х отрезка [a,b], можно рассматривать как всевозможные элементарные исходы некоторого испытания. Пусть событие А состоит в том, что результат испытания принадлежит отрезку [ α, β] Ì [a, b]. Тогда точки отрезка [ α, β] есть благоприятные элементарные исходы события А. Согласно формуле (2.9) имеем геометрическое определение вероятности: под вероятностью события А понимается отношение меры множества элементарных исходов, благоприятствующих событию А, к мере L множества всех возможных элементарных исходов в предположении, что они равновозможны: Это определение естественно переносит классическое определение вероятности на случай бесконечного числа элементарных исходов (случаев). Аналогичное определение можно ввести также тогда, когда элементарные исходы испытания представляют собой точки плоскости или пространства. Задача. В течение часа 0 ≤ t ≤ 1 (t – время в часах) на остановку прибывает один и только один автобус. Какова вероятность того, что пассажиру, пришедшему на эту остановку в момент времени t = 0, придется ожидать автобус не более 10 минут? Решение . Здесь множество всех элементарных исходов образует отрезок [0,1], временная длина которого L =1, а множество благоприятных элементарных исходов составляет отрезок [0,1/6] временной длины =1/6. Поэтому искомая вероятность есть Задача. В квадрат К со стороной а с вписанным в него кругом S (рис. 3.10) случайно бросается материальная точка М. Какова вероятность того, что эта точка попадает в круг S? 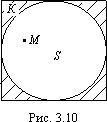 Решение . Здесь площадь квадрата К =а в2, а площадь круга За искомую вероятность естественно принять отношение Эта вероятность, а следовательно, и число π, очевидно, могут быть определены экспериментально. Показательное распределение Непрерывная случайная величина Х, функция плотности которой задается выражением называется случайной величиной, имеющей показательное, или экспоненциальное, распределение. Здесь параметр λ постоянная положительная величина. Величина срока службы различных устройств и времени безотказной работы отдельных элементов этих устройств при выполнении определенных условий обычно подчиняется показательному распределению. Также этому распределению подчиняется время ожидания клиента в системе массового обслуживания (магазин, мастерская, банк, парикмахерская и т.д.). Другими словами, величина промежутка времени между появлениями двух последовательных редких событий подчиняется зачастую показательному распределению. График дифференциальной функции показательного распределения показан 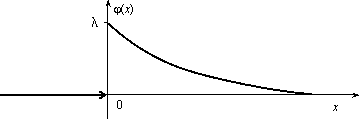 Нормальное распределение Случайная величина Х имеет нормальное распределение (или распределение по закону Гаусса), если ее плотность вероятности имеет вид: где параметры а – любое действительное число и σ >0. График дифференциальной функции нормального распределения называют нормальной кривой (кривой Гаусса). Нормальная кривая (рис. 2.12) симметрична относительно прямой х =а, имеет максимальную ординату , а в точках х = а ± σ – перегиб. 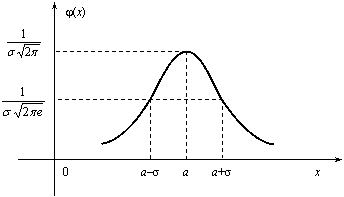 Доказано, что параметр а является математическим ожиданием (также модой и медианой), а σ – средним квадратическим отклонением. Коэффициенты асимметрии и эксцесса для нормального распределения равны нулю: As = Ex = 0. Установим теперь, как влияет изменение параметров а и σ на вид нормальной кривой. При изменении параметра а форма нормальной кривой не изменяется. В этом случае, если математическое ожидание (параметр а) уменьшилось или увеличилось, график нормальной кривой сдвигается влево или вправо (рис. 2.13). При изменении параметра σ изменяется форма нормальной кривой. Если этот параметр увеличивается, то максимальное значение функции убывает, и наоборот. Так как площадь, ограниченная кривой распределения и осью Ох, должна быть постоянной и равной 1, то с увеличением параметра σ кривая приближается к оси Ох и растягивается вдоль нее, а с уменьшением σ кривая стягивается к прямой х = а (рис. 2.14). 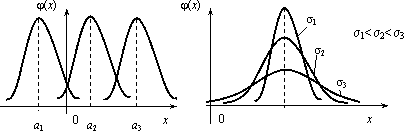 Функция плотности нормального распределения φ(х) с параметрами а = 0, σ = 1 называется плотностью стандартной нормальной случайной величины, а ее график – стандартной кривой Гаусса. Функция плотности нормальной стандартной величины определяется формулой 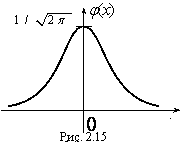 . .Из свойств математического ожидания и дисперсии следует, что для величины , D(U)=1, M(U) = 0. Поэтому стандартную нор мальную кривую можно рассматривать как кривую распределения случайной величины , где Х – случайная величина, подчиненная нормальному закону распределения с параметрами а и σ. Нормальный закон распределения случайной величины в интегральной форме имеет вид (2.10) Полагая в интеграле (3.10) , получим , Где . Первое слагаемое равно 1/2 (половине площади криволинейной трапеции, изображенной на рис. 3.15). Второе слагаемое называется функцией Лапласа, а также интегралом вероятности. Поскольку интеграл в формуле (2.11) не выражается через элементарные функции, для удобства расчетов составлена для z ≥ 0 таблица функции Лапласа. Чтобы вычислить функцию Лапласа для отрицательных значений z, необходимо воспользоваться нечетностью функции Лапласа: Ф(–z) = – Ф(z). Окончательно получаем расчетную формулу Отсюда получаем, что для случайной величины Х, подчиняющейся нормальному закону, вероятность ее попадания на отрезок [ α, β] есть 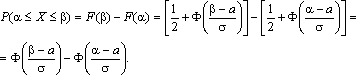 С помощью формулы предыдущей найдем вероятность того, что модуль отклонения нормального распределения величины Х от ее центра распределения а меньше 3σ. Имеем Р(|x – a| < 3 s) =P(а–3 s< X< а+3 s)= Ф(3) – Ф(–3) = 2Ф(3) »0,9973. Значение Ф(3) получено по таблице функции Лапласа. Принято считать событие практически достоверным, если его вероятность близка к единице, и практически невозможным, если его вероятность близка к нулю. Мы получили так называемое правило трех сигм: для нормального распределения событие (|x–a| < 3σ) практически достоверно. Правило трех сигм можно сформулировать иначе: хотя нормальная случайная величина распределена на всей оси х, интервал ее практически возможных значений есть (a–3σ, a+3σ). Нормальное распределение имеет ряд свойств, делающих его одним из самых употребительных в статистике распределений. Если предоставляется возможность рассматривать некоторую случайную величину как сумму достаточно большого числа других случайных величин, то данная случайная величина обычно подчиняется нормальному закону распределения. Суммируемые случайные величины могут подчиняться каким угодно распределениям, но при этом должно выполняться условие их независимости (или слабой независимости). Также ни одна из суммируемых случайных величин не должна резко отличаться от других, т.е. каждая из них должна играть в общей сумме примерно одинаковую роль и не иметь исключительно большую по сравнению с другими величинами дисперсию. Этим и объясняется широкая распространенность нормального распределения. Оно возникает во всех явлениях, процессах, где рассеяния случайной изучаемой величины вызывается большим количеством случайных причин, влияние каждой из которых в отдельности на рассеяние ничтожно мало. Большинство встречающихся на практике случайных величин (таких, например, как количества продаж некоторого товара, ошибка измерения; отклонение снарядов от цели по дальности или по направлению; отклонение действительных размеров деталей, обработанных на станке, от номинальных размеров и т.д.) может быть представлено как сумма большого числа независимых случайных величин, оказывающих равномерно малое влияние на рассеяние суммы. Такие случайные величины принято считать нормально распределенными. Гипотеза о нормальности подобных величин находит свое теоретическое обоснование в центральной предельной теореме и получила многочисленные практические подтверждения. Представим себе, что некоторый товар реализуется в нескольких торговых точках. Из–за случайного влияния различных факторов количества продаж товара в каждой точке будут несколько различаться, но среднее всех значений будет приближаться к истинному среднему числу продаж. Отклонения числа продаж в каждой торговой точке от среднего образуют симметричную кривую распределения, близкую к кривой нормального распределения. Любое систематическое влияние какого-либо фактора проявится в асимметрии распределения. Задача . Случайная величина распределена нормально с параметрами а = 8, σ = 3.Найти вероятность того, что случайная величина в результате опыта примет значение, заключенной в интервале (12,5; 14). Решение. Воспользуемся формулой (2.12). Имеем Задача . Число проданного за неделю товара определенного вида Х можно считать распределенной нормально. Математическое ожидание числа продаж тыс. шт. Среднее квадратическое отклонение этой случайной величины σ = 0,8 тыс. шт. Найти вероятность того, что за неделю будет продано от 15 до 17 тыс. шт. товара. Решение. Случайная величина Х распределена нормально с параметрами а = М(Х) = 15,7; σ = 0,8. Требуется вычислить вероятность неравенства 15 ≤ X ≤ 17. По формуле (2.12) получаем 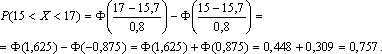 Элементы математической статистики Установление закономерностей, которым подчинены массовые случайные явления, основано на изучении методами теории вероятностей статистических данных - результатов наблюдений. Статистические данные представляют собой данные, полученные в результате обследования большого числа объектов или явлений; следовательно, математическая статистика имеет дело с массовыми явлениями. Первая задача математической статистики - указать способы сбора и группировки статистических сведений, полученных в результате наблюдений или в результате специально поставленных экспериментов. Вторая задача математической статистики - разработать методы анализа статистических данных в зависимости от целей исследования. Современная математическая статистика разрабатывает способы определения числа необходимых испытаний до начала исследования, в ходе исследования и решает многие другие задачи. Современную математическую статистику определяют как науку о принятии решений в условиях неопределенности Итак, задача математической статистики состоит в создании методов сбора и обработки статистических данных для получения научных и практических выводов. Генеральная и выборочная совокупность статистических данных Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Качественными признаками объект обладает либо не обладает. Они не поддаются непосредственному измерению (например, спортивная специализация, квалификация, национальность, территориальная принадлежность и т. п.). Количественные признаки представляют собой результаты подсчета или измерения. В соответствии с этим они делятся на дискретные и непрерывные. Иногда проводиться сплошное обследование, т.е. обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике сплошное обследование применяют сравнительно редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению. Различают генеральную и выборочную совокупности. Выборочной совокупностью (выборкой) называют совокупность случайно отобранных объектов. Генеральной (основной) совокупностью называют совокупность, объектов из которых производится выборка. Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности N = 1000, а объем выборки n =100. Число объектов генеральной совокупности N значительно превосходит объем выборки n . Способы выборки При составлении выборки можно поступать двумя способами: после того как объект отобран и над ним произведено наблюдение, он может быть возвращен либо не возвращен в генеральную совокупность. В соответствии со сказанным выборки подразделяют на повторные и бесповторные. Повторной называют выборку, при которой отобранный объект (перед отбором следующего) возвращается в генеральную совокупность. Бесповторной называют выборку, при которой отобранный объект в генеральную совокупность не возвращается. На практике обычно пользуются бесповторным случайным отбором. Для того чтобы по данным выборки можно было достаточно уверенно судить об интересующем признаке генеральной совокупности, необходимо, чтобы объекты выборки правильно его представляли (выборка должна правильно представлять пропорции генеральной совокупности) - выборка должна быть репрезентативной (представительной). Выборка будет репрезентативной, если: каждый объект выборки отобран случайно из генеральной совокупности; все объекты имеют одинаковую вероятность попасть в выборку. Обычно полученные наблюдаемые данные представляют собой множество расположенных в беспорядке чисел. Просматривая это множество чисел, трудно выявить какую-либо закономерность их варьирования (изменения). Для изучения закономерностей варьирования значений случайной величины опытные данные подвергают обработке. Пример 1. Проводились наблюдения над числом Х оценок полученных студентами ВУЗа на экзаменах. Наблюдения в течение часа дали следующие результаты: 3; 4; 3; 5; 4; 2; 2; 4; 4; 3; 5; 2; 4; 5; 4; 3; 4; 3; 3; 4; 4; 2; 2; 5; 5; 4; 5; 2; 3; 4; 4; 3; 4; 5; 2; 5; 5; 4; 3; 3; 4; 2; 4; 4; 5; 4; 3; 5; 3; 5; 4; 4; 5; 4; 4; 5; 4; 5; 5; 5. Здесь число Х является дискретной случайной величиной, а полученные о ней сведения представляют собой статистические (наблюдаемые) данные. Расположив приведенные выше данные в порядке неубывания и сгруппировав их так, что в каждой отдельной группе значения случайной величины будут одинаковы, получают ранжированный ряд данных наблюдения. В примере 1 имеем четыре группы со следующими значениями случайной величины: 2; 3; 4; 5. Значение случайной величины, соответствующее отдельной группе сгруппированного ряда наблюдаемых данных, называют вариантом, а изменение этого значения варьированием. Варианты обозначают малыми буквами латинского алфавита с соответствующими порядковому номеру группы индексами - xi. Число, которое показывает, сколько раз встречается соответствующий вариант в ряде наблюдений называют частотой варианта и обозначают соответственно - ni. Сумма всех частот ряда Статистическим распределением выборки называют перечень вариантов и соответствующих им частот или относительных частот (табл. 1, табл. 2). Пример 2. Задано распределение частот выборки объема n = 20:
Написать распределение относительных частот. Решение. Найдем относительные частоты, для чего разделим частоты на объем выборки: W1 = 3/20 = 0,15; W2 = 10/20 = 0,50; W3 = 7/20 = 0,35. Напишем распределение относительных частот:
Контроль: 0,15 + 0,50 + 0, 35 = 1. Статистическое распределение можно задать также в виде последовательности интервалов и соответствующих им частот (в качестве частоты, соответствующей интервалу, принимают сумму частот, попавших в этот интервал). Дискретным вариационным рядом распределения называют ранжированную совокупность вариантов xi с соответствующими им частотами ni или относительными частотами wi. Для рассмотренного выше примера 1 дискретный вариационный ряд имеет вид:
Контроль: сумма всех частот вариационного ряда (сумма значений второй строки таблицы 3) есть объем выборки (в примере 1 n = 60 ); сумма относительных частот вариационного ряда должна быть равна 1 (сумма значений третьей строки таблицы. Интервальный вариационный ряд Если изучаемая случайная величина является непрерывной, то ранжирование и группировка наблюдаемых значений зачастую не позволяют выделить характерные черты варьирования ее значений. Это объясняется тем, что отдельные значения случайной величины могут как угодно мало отличаться друг от друга и поэтому в совокупности наблюдаемых данных одинаковые значения величины могут встречаться редко, а частоты вариантов мало отличаются друг от друга. Нецелесообразно также построение дискретного ряда для дискретной случайной величины, число возможных значений которой велико. В подобных случаях следует строить интервальный вариационный ряд распределения. Для построения такого ряда весь интервал варьирования наблюдаемых значений случайной величины разбивают на ряд частичных интервалов и подсчитывают частоту попадания значений величины в каждый частичный интервал. Интервальным вариационным рядом называют упорядоченную совокупность интервалов варьирования значений случайной величины с соответствующими частотами или относительными частотами попаданий в каждый из них значений величины. Для построения интервального ряда необходимо: определить величину частичных интервалов; определить ширину интервалов; установить для каждого интервала его верхнюю и нижнюю границы; сгруппировать результаты наблюдении. 1. Вопрос о выборе числа и ширины интервалов группировки приходится решать в каждом конкретном сkучае исходя из целей исследования, объема выборки и степени варьирования признака в выборке. Приблизительно число интервалов k можно оценить исходя только из объема выборки n одним из следующих способов: по формуле Стержеса: k = 1 + 3,32·lg n; с помощью таблицы 1.
2. Обычно предпочтительны интервалы одинаковой ширины. Для определения ширины интервалов h вычисляют: размах варьирования R - значений выборки: R = xmax - xmin, где xmax и xmin - максимальная и минимальная варианты выборки; ширину каждого из интервалов h определяют по следующей формуле: h = R/k. 3. Нижняя граница первого интервала xh1 выбирается так, чтобы минимальная варианта выборки xmin попадала примерно в середину этого интервала: xh1 = xmin - 0,5·h . Промежуточные интервалы получают прибавляя к концу предыдущего интервала длину частичного интервала h: xhi = xhi-1 +h . Построение шкалы интервалов на основе вычисления границ интервалов продолжается до тех пор, пока величина xhi удовлетворяет соотношению: xhi < xmax + 0,5·h . 4. В соответствии со шкалой интервалов производится группирование значений признака - для каждого частичного интервала вычисляется сумма частот ni вариант, попавших в i-й интервал. При этом в интервал включают значения случайной величины, большие или равные нижней границе и меньшие верхней границы интервала. Полигон и гистограмма Для наглядности строят различные графики статистического распределения. По данным дискретного вариационного ряда строят полигон частот или относительных частот. Полигоном частот называют ломанную, отрезки которой соединяют точки (x1; n1), (x2; n2), ..., (xk; nk). Для построения полигона частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им частоты ni. Точки ( xi; ni) соединяют отрезками прямых и получают полигон частот (Рис. 1). Полигоном относительных частот называют ломанную, отрезки которой соединяют точки (x1; W1), (x2; W2), ..., (xk; Wk). Для построения полигона относительных частот на оси абсцисс откладывают варианты xi, а на оси ординат - соответствующие им относительные частоты Wi. Точки ( xi; Wi) соединяют отрезками прямых и получают полигон относительных частот. В случае непрерывного признака целесообразно строить гистограмму. Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению ni / h (плотность частоты). Для построения гистограммы частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии ni / h. Площадь i - го частичного прямоугольника равна hni / h = ni - сумме частот вариант i - го интервала; следовательно, площадь гистограммы частот равна сумме всех частот, т.е. объему выборки. Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению Wi / h (плотность относительной частоты). Для построения гистограммы относительных частот на оси абсцисс откладывают частичные интервалы, а над ними проводят отрезки, параллельные оси абсцисс на расстоянии Wi / h (Рис. 2). Площадь i - го частичного прямоугольника равна hWi / h = Wi - относительной частоте вариант попавших в i - й интервал. Следовательно, площадь гистограммы относительных частот равна сумме всех относительных частот, т.е. единице. |
