Теория Вероятности. Реферат по дисциплине теория вероятности Ручина Н. А гр 10менз Проверил Гладков В. В нижний Новгород, 2011
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
Замечание: n!=1*2*3*...*n (читается: "эн факториал"), кроме того полагают, что 0!=1. Пример 5. Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различные и нечетные? Решение: т.к. нечетных цифр пять, а именно 1, 3, 5, 7, 9, то эта задача сводится к выбору и размещению на две разные позиции двух из пяти различных цифр, т.е. указанных чисел будет: Определение 2. Сочетанием из n элементов по m называется любой неупорядоченный набор из m различных элементов, выбранных из генеральной совокупности в n элементов. Пример 6. Для множества {1, 2, 3}сочетаниями являются {1, 2}, {1, 3}, {2, 3}. Число сочетаний обозначается Cnm и вычисляется по формуле: Определение 3. Перестановкой из n элементов называется любой упорядоченный набор этих элементов. Пример 7a. Всевозможными перестановками множества, состоящего из трех элементов {1, 2, 3} являются: (1, 2, 3), (1, 3, 2), (2, 3, 1), (2, 1, 3), (3, 2, 1), (3, 1, 2). Число различных перестановок из n элементов обозначается Pn и вычисляется по формуле Pn=n!. Пример 8. Сколькими способами семь книг разных авторов можно расставить на полке в один ряд? Решение: эта задача о числе перестановок семи разных книг. Имеется P7=7!=1*2*3*4*5*6*7=5040 способов осуществить расстановку книг. Обсуждение. Мы видим, что число возможных комбинаций можно посчитать по разным правилам (перестановки, сочетания, размещения) причем результат получится различный, т.к. принцип подсчета и сами формулы отличаются. Внимательно посмотрев на определения, можно заметить, что результат зависит от нескольких факторов одновременно. Во-первых, от того, из какого количества элементов мы можем комбинировать их наборы (насколько велика генеральная совокупность элементов). Во-вторых, результат зависит от того, какой величины наборы элементов нам нужны. И последнее, важно знать, является ли для нас существенным порядок элементов в наборе. Поясним последний фактор на следующем примере. Пример. На родительском собрании присутствует 20 человек. Сколько существует различных вариантов состава родительского комитета, если в него должны войти 5 человек? Решение: В этом примере нас не интересует порядок фамилий в списке комитета. Если в результате в его составе окажутся одни и те же люди, то по смыслу для нас это один и тот же вариант. Поэтому мы можем воспользоваться формулой для подсчета числа сочетаний из 20 элементов по 5. Иначе будут обстоять дела, если каждый член комитета изначально отвечает за определенное направление работы. Тогда при одном и том же списочном составе комитета, внутри него возможно 5! вариантов перестановок, которые имеют значение. Количество разных (и по составу, и по сфере ответственности) вариантов определяется в этом случае числом размещений из 20 элементов по 5. Геометрическое определение вероятности Пусть случайное испытание можно представить себе как бросание точки наудачу в некоторую геометрическую область G (на прямой, плоскости или пространстве). Элементарные исходы – это отдельные точки G, любое событие – это подмножество этой области, пространства элементарных исходов G. Можно считать, что все точки G «равноправны» и тогда вероятность попадания точки в некоторое подмножество пропорционально его мере (длине, площади, объему) и не зависит от его расположения и формы. Геометрическая вероятность события А определяется отношением: Пример. На плоскость, разграфленную параллельными полосами шириной 2d, расстояние между осевыми линиями которых равно 2D, наудачу брошен круг радиуса r ( Решение. В качестве элементарного исхода этого испытания будем считать расстояние x от центра круга до осевой линии ближайшей к кругу полосы. Тогда все пространство элементарных исходов – это отрезок Для искомой вероятности получаем: Классификация событий на возможные, вероятные и случайные. Понятия простого и сложного элементарного события. Операции над событиями. Классическое определение вероятности случайного события и её свойства. Элементы комбинаторики в теории вероятностей. Геометрическая вероятность. Аксиомы теории вероятностей. 1. Классификация событий Одним из основных понятий теории вероятностей является понятие события. Под событием понимают любой факт, который может произойти в результате опыта или испытания. Под опытом, или испытанием, понимается осуществление определённого комплекса условий. Примеры событий: – попадание в цель при выстреле из орудия (опыт — произведение выстрела; событие — попадание в цель); – выпадение двух гербов при трёхкратном бросании монеты (опыт — трёхкратное бросание монеты; событие - выпадение двух гербов); – появление ошибки измерения в заданных пределах при измерении дальности до цели (опыт - измерение дальности; событие — ошибка измерения). Можно привести бесчисленное множество подобных примеров. События обозначаются заглавными буквами латинского алфавита Различают события совместные и несовместные. События называются совместными, если наступление одного из них не исключает наступления другого. В противном случае события называются несовместными. Например, подбрасываются две игральные кости. Событие — выпадание трех очков на первой игральной кости, событие — выпадание трех очков на второй кости. и — совместные события. Пусть в магазин поступила партия обуви одного фасона и размера, но разного цвета. Событие — наудачу взятая коробка окажется с обувью черного цвета, событие — коробка окажется с обувью коричневого цвета, и — несовместные события. Событие называется достоверным, если оно обязательно произойдет в условиях данного опыта. Событие называется невозможным, если оно не может произойти в условиях данного опыта. Например, событие, заключающееся в том, что из партии стандартных деталей будет взята стандартная деталь, является достоверным, а нестандартная — невозможным. Событие называется возможным, или случайным, если в результате опыта оно может появиться, но может и не появиться. Примером случайного события может служить выявление дефектов изделия при контроле партии готовой продукции, несоответствие размера обрабатываемого изделия заданному, отказ одного из звеньев автоматизированной системы управления. События называются равновозможными, если по условиям испытания ни одно из этих событий не является объективно более возможным, чем другие. Например, пусть магазину поставляют электролампочки (причем в равных количествах) несколько заводов-изготовителей. События, состоящие в покупке лампочки любого из этих заводов, равновозможны. Важным понятием является полная группа событий. Несколько событий в данном опыте образуют полную группу, если в результате опыта обязательно появится хотя бы одно из них. Например, в урне находится десять шаров, из них шесть шаров красных, четыре белых, причем пять шаров имеют номера. — появление красного шара при одном извлечении, — появление белого шара, — появление шара с номером. События Введем понятие противоположного, или дополнительного, события. Под противоположным событием понимается событие, которое обязательно должно произойти, если не наступило некоторое событие . Противоположные события несовместны и единственно возможны. Они образуют полную группу событий. Например, если партия изготовленных изделий состоит из годных и бракованных, то при извлечении одного изделия оно может оказаться либо годным — событие , либо бракованным — событие . 2. Операции над событиями При разработке аппарата и методики исследования случайных событий в теории вероятностей очень важным является понятие суммы и произведения событий. Суммой, или объединением, нескольких событий называется событие, состоящее в наступлении хотя бы одного из этих событий. Сумма событий Например, если событие А есть попадание в цель при первом выстреле, событие В— при втором, то событие Произведением, или пересечением, нескольких событий называется событие, состоящее в совместном появлении всех этих событий. Произведение событий . Например, если событие А есть попадание в цель при первом выстреле, событие В — при втором, то событие Понятия суммы и произведения событий имеют наглядную геометрическую интерпретацию. Пусть событие А состоит в попадании точки в область А , событие В— в попадании в область В, тогда событие 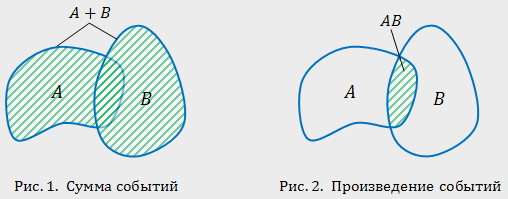 Статистическое определение вероятности Формулу (1.1) используют для непосредственного вычисления вероятностей событий только тогда, когда опыт сводится к схеме случаев. На практике часто классическое определение вероятности неприменимо по двум причинам: во-первых, классическое определение вероятности предполагает, что общее число случаев должно быть конечно. На самом же деле оно зачастую не ограничено. Во-вторых, часто невозможно представить исходы опыта в виде равновозможных и несовместных событий.[/indent] Частота появления событий при многократно повторяющихся Опытах имеет тенденцию стабилизироваться около какой-то постоянной величины. Таким образом, с рассматриваемым событием можно связать некоторую постоянную величину, около которой группируются частоты и которая является характеристикой объективной связи между комплексом условий, при которых проводятся опыты, и событием. Вероятностью случайного события называется число, около которого группируются частоты этого события по мере увеличения числа испытаний. Это определение вероятности называется статистическим. Преимущество статистического способа определения вероятности состоит в том, что он опирается на реальный эксперимент. Однако его существенный недостаток заключается в том, что для определения вероятности необходимо выполнить большое число опытов, которые очень часто связаны с материальными затратами. Статистическое определение вероятности события хотя и достаточно полно раскрывает содержание этого понятия, но не дает возможности фактического вычисления вероятности. Решение задачи: При испытании партии приборов относительная частота годных приборов оказалась равной 0,9. Найти число годных приборов, если всего было проверено 200 приборов. Дано: W(A)= 0,9; n = 200, m – ? Используемые формулы: m = W(A) n Решение: m = 0,9 x 200 = 180 Ответ: 180 годных приборов Решение задачи № 5 аналогичным способом В пакете 25 разных конфет. Какова вероятность того, что выбранные на удачу три конфеты будут именно те, которые Вы хотели? Решение. Используемые формулы 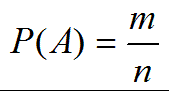 , , m - число исходов испытания , благоприятствующих наступлению события А, n - общее число всех равновозможных несовместных исходов 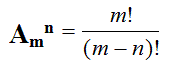 n – число элементов, входящих в каждую комбинацию; m – число всех имеющихся элементов 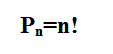 n – число элементов, входящих в каждую перестановку, (n - натуральное число) 1. Найдем n - общее число всех равновозможных несовместных исходов при вытягивании трех конфет. Их будет столько, сколько можно составить различных размещений из 25 элементов по три: 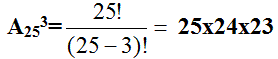 2. Найдем m. Число случаев, благоприятствующих тому, что будут выбраны нужные три конфеты, столько, сколько можно составить перестановок из трех элементов Р3= 3!= 1 х 2 х 3 = 6. 3. Искомая вероятность равна 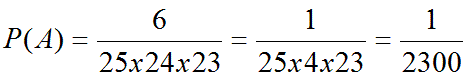 Ответ: вероятность 1/2300 Аксиоматическое определение вероятности Пусть Ω - множество всех возможных исходов некоторого опыта (эксперимента). Согласно аксиоматическому определению вероятности, каждому события А (А подмножество множества Ω) ставится в соответствии некоторое числу р(А), называемое вероятностью события А, причем так, что выполняются следующие три условия (аксиомы вероятностей): р(А)≥0 p(Ω)=1 аксиома сложения 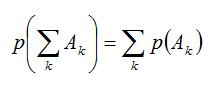 где Аi·Aj=Ω (i≠j), т.е. вероятность суммы попарно-несовместных событий равна сумме вероятностей этих событий. Из этих трех аксиом, вытекают свойства вероятности: р(Ø)=0, т.е. вероятность невозможного события равна нулю. р(А)+р(Ā)=1 0≤р(А)≤1 для любого события А р(А)≤р(В), если А подмножество В 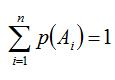 , если , если 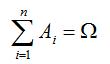 и Аi·Aj=Ø, i≠j Если множество Ω состоит из n равновозможных элементарных событий, то вероятность события А определяется по формуле классического определения вероятности: p(A)=m/n где m - число случаев (элементов), принадлежащих множеству В (число блогаприятствующих событию А исходов), n - число элементов множества Ω (число всех исходов опыта). Таким образом, мы дали определение вероятности: классическое определение вероятности, геометрическое определение вероятности и аксиоматическое определение вероятности Пример: На отрезке [0, 1] наугад (случайно) поставлена точка. Измеряется расстояние точки от левого конца отрезка. В этом опыте пространство элементарных событий W = [0, 1] - множество действительных чисел на единичном отрезке. В более точных, формальных терминах элементарные события и пространство элементарных событий описывают следующим образом. Пространством элементарных событий называют произвольное множество W, W ={w}. Элементы w этого множества W называют элементарными событиями. Понятия элементарное событие, событие, пространство элементарных событий, являются первоначальными понятиями теории вероятностей. Невозможно привести более конкретное описание пространства элементарных событий. Для описания каждой реальной модели выбирается соответствующее пространство W. Событие W называется достоверным событием. Достоверное событие не может не произойти в результате эксперимента, оно происходит всегда. Пример 4. Бросаем один раз игральную кость. Достоверное событие состоит в том, что выпало число очков, не меньше единицы и не больше шести, т.е. W = {w 1, w 2, w 3, w 4, w 5, w 6}, где w i- выпадение i очков, - достоверное событие. Невозможным событием называется пустое множество . Невозможное событие не может произойти в результате эксперимента, оно не происходит никогда. Случайное событие может произойти или не произойти в результате эксперимента, оно происходит иногда. Формула полной вероятности. Формулы Байеса Пусть A - произвольное событие, а события B1, B2, …, Bn - попарно несовместны и образуют полную группу событий, т.е. . Тогда имеет место следующая формула для вероятности события A - формула полной вероятности - Если событие A произошло, то вероятность того, что имело место событие Bk вычисляется по формуле Байеса: . |
