реферат по физике. Реферат по физике на тему "Изучение равновесных и квазиравновесных термодинамических процессов и экспериментальное определение показателя адиабаты воздуха "
 Скачать 1.27 Mb. Скачать 1.27 Mb.
|
|
Федеральное агентство морского и речного транспорта Федерального бюджетного общеобразовательное учреждение высшего профессионального образования "Волжская государственная академия водного транспорта" Кафедра эксплуатации судовых энергетических установок Реферат по физике на тему "Изучение равновесных и квазиравновесных термодинамических процессов и экспериментальное определение показателя адиабаты воздуха " Выполнил: Студент группы ЗСМ(1) Тымбай А.С Проверил: Бубнов Е.Я Дайте определение идеального газа. Запишите уравнение Менделеева-Клапейрона, связывающее параметры состояния идеального газа. Идеальный газ Наиболее простым из всех агрегатных состояний вещества является газообразное. Поэтому изучение свойств веществ начинают с газов. Газ (греч. chaos — хаос) — такое агрегатное состояние вещества, когда составляющие его частицы почти свободно и хаотически движутся между соударениями, во время которых происходит резкое изменение их скорости. Термин «газ» предложил в начале XVII в. нидерландский химик Ян Батист ван Гельмонт (1579— 1644). Для теоретического объяснения свойств газов используют их упрощённую модель — идеальный газ. Идеальный газ — модель газа, удовлетворяющая следующим условиям: 1) молекулы газа можно считать материальными точками, которые хаотически движутся; 2) силы взаимодействия между молекулами идеального газа практически отсутствуют (потенциальная энергия их взаимодействия равна нулю); силы действуют только во время столкновений молекул, причём это силы отталкивания. Поведение молекул идеального газа можно описать, используя законы Ньютона и учитывая, что между соударениями молекулы движутся практически равномерно и прямолинейно. Модель идеального газа можно использовать в ограниченном диапазоне температур и при достаточно малых давлениях. Так, например, свойства водорода и гелия при нормальном атмосферном давлении и комнатной температуре близки к свойствам идеального газа.  Изучая физику в 7-м классе, вы узнали, что давление газа на стенки сосуда, в котором он находится, как и на любое тело, помещённое внутрь сосуда, создаётся в результате ударов частиц, образующих газ (рис. 14). Вследствие хаотичности их движения усреднённое по времени давление газа в любой части сосуда одинаково, и его можно определить по формуле. Уравнение Клапейрона-Менделеева (1834 г) устанавливает связь между объемом V, давлением P и абсолютной температурой Т для газа: PV = nRT, где: n – число молей газа P – давление газа, Па; V – объем газа, м3; T – абсолютная температура газа, К; R – универсальная газовая постоянная 8,314 Дж/моль×K. Если объём газа выражен в литрах, то уравнение Клапейрона-Менделеева записывается в виде: Из уравнения Клапейрона-Менделеева следует три закона: 1. Закон Шарля: 2. Закон Гей-Люссака: 3. Закон Болйя-Мариотта: Дайте определение изопроцессов и адиабатного процесса, напишите уравнения этих процессов, графически изобразите их на диаграмме состояний. Выведите уравнение адиабатического процесса (уравнение Пуассона) Изопроцессы — термодинамические процессы, во время которых количество вещества и ещё одна из физических величин — параметров состояния: давление, объём или температура — остаются неизменными. 1. Изотермический процесс. Изменение внутренней энергии при изотермическом процессе не происходит. Все количество теплоты, переданное системе, согласно формуле (48), идет на совершение работы: ΔQ=A. ( 2. Изобарный процесс - процесс, протекающий при постоянном давлении. Первое начало термодинамики для изобарного процесса: процесс изменения состояния термодинамической системы при постоянном давлении ( 3. Изохорный процесс. При изохорном процессе газ не совершает работы. Первое начало термодинамики для изохорного процесса: ΔQ=ΔU. процесс изменения состояния термодинамической системы при постоянном объёме ( 4. Адиабатический процесс - процесс, при котором отсутствует теплообмен между системой и окружающей средой (ΔQ=0). Все быстропротекающие процессы можно отнести к адиабатическим. Уравнения состояний системы для адиабатического процесса: PVλ=const - уравнение Пуассона  Уравнение адиабатического процесса (уравнение Пуассона)  Сформулируйте первый закон (начало) термодинамики. Объясните каждую из величин Q, ΔU, A (δQ, dU, δA)входящую в этот закон. От каких параметров состояния идеального газа зависят эти величины. Запишите первое начало термодинамики для изопроцессов и адиабатного процесса. Первый закон термодинамики: При изучении физики в 9 классе вы узнали, что полная механическая энергия замкнутой системы тел сохраняется только при отсутствии трения, а при наличии трения она уменьшается. Куда девается механическая энергия? Если бутылку, заполненную до половины водой при комнатной температуре, встряхивать в течение нескольких минут, то окажется, что вода нагрелась на 1—2 °С. Каким образом нагрелась вода? В середине XIX века известный английский физик Дж. Джоуль (1818— 1889), проведя многочисленные опыты, показал, что совершённая при перемешивании воды механическая работа практически равна увеличению её внутренней энергии. Опыты Джоуля, а также исследования немецкого врача и естествоиспытателя Р. Майера (1814—1878), немецкого профессора физиологии и одного из самых знаменитых физиков второй половины XIX века Г. Гельмгольца (1821 —1894) позволили сформулировать закон сохранения и превращения энергии, распространив его на все явления природы. Согласно этому закону при любых взаимодействиях материальных объектов энергия не исчезает и не возникает из ничего, она только передаётся от одних объектов к другим или превращается из одной формы в другую. Для термодинамических систем (в термодинамике обычно рассматривают макроскопически неподвижные системы) закон сохранения и превращения энергии называют первым законом термодинамики. Согласно первому закону термодинамики, приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного или отданного системой при взаимодействии с внешними телами: Поскольку работа внешних сил равна работе, совершаемой термодинамической системой, взятой с противоположным знаком ( Если система представляет собой действующее устройство, периодически возвращающееся в исходное состояние, то при этом AU-0 и A-Q. Механизм, который мог бы совершать работу без изменения состояния составляющих его тел и без теплопередачи от внешних тел, называют «вечным двигателем первого рода». Поэтому первый закон термодинамики можно сформулировать и следующим образом: невозможен вечный двигатель первого рода, т. е. такой двигатель, который при неизменном значении собственной внутренней энергии совершал бы работу большую, чем энергия, получаемая им извне. Применим первый закон термодинамики к различным изопроцессам, происходящим с идеальным одноатомным газом. Изохорный процесс Пусть идеальный одноатомный газ находится в цилиндрическом сосуде, закрытом неподвижным поршнем (V = const). Нагреем сосуд с газом. Объём газа остаётся практически постоянным (тепловым расширением сосуда пренебрегаем) (рис. 60), следовательно, работа силы давления газа А= 0. Тогда первый закон термодинамики примет вид Это означает, что всё передаваемое газу количество теплоты идёт на увеличение его внутренней энергии. При этом приращение внутренней энергии газа 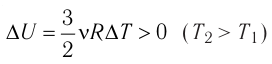 (рис. 61, а). А если газ при изохорном (рис. 61, а). А если газ при изохорном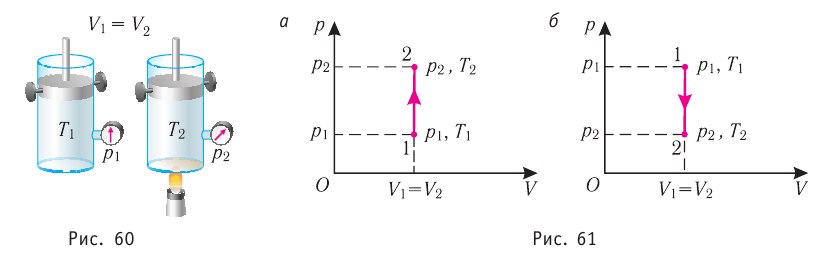 процессе отдаёт количество теплоты, то его внутренняя энергия убывает: 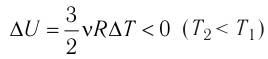 (рис. 61, б). (рис. 61, б).Изотермический процесс Пусть цилиндрический сосуд с газом под поршнем находится в термостате — устройстве, в котором поддерживается постоянная температура. В этом случае внутренняя энергия идеального одноатомного газа  остаётся постоянной, а её изменение остаётся постоянной, а её изменение Какие выводы следуют из этого? Если с помощью внешнего устройства медленно перемещать поршень в сосуде так, чтобы объём газа увеличивался (  Если же внешнее устройство обеспечивает медленное уменьшение объёма газа в сосуде ( Изобарный процесс Пусть газ находится в цилиндрическом сосуде, закрытом поршнем, который может свободно или под постоянной нагрузкой перемещаться (рис. 64). Нагреем газ, передав ему некоторое количество теплоты (Q > 0). Согласно первому закону термодинамики (11.2) переданное газу количество теплоты частично расходуется на увеличение внутренней энергии При изобарном процессе работа расширения (сжатия) газа 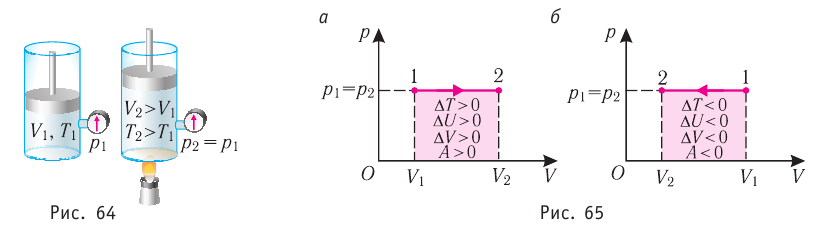 При изобарном сжатии газа внешние силы совершают работу А' > 0. Чтобы давление газа при этом оставалось постоянным, газ необходимо охлаждать, т. е. он должен отдавать в окружающую среду некоторое количество теплоты (Q < 0). Понижение температуры газа при изобарном сжатии приводит к уменьшению его внутренней энергии ( Удельная теплоёмкость вещества зависит не только от его свойств, но и от характера осуществления процесса теплопередачи. Действительно, из формулы (10.4) следует, что удельная теплоемкость 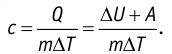 Тогда согласно первому закону термодинамики при изохорном процессе (11.3) удельная теплоёмкость идеального газа 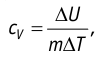 а при изобарном (11.5) — а при изобарном (11.5) —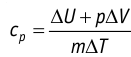 Таким образом, для одинакового увеличения температуры при изобарном нагревании единице массы газа необходимо передать большее количество теплоты, чем при изохорном нагревании, т. е. Таким образом, для одинакового увеличения температуры при изобарном нагревании единице массы газа необходимо передать большее количество теплоты, чем при изохорном нагревании, т. е. Это объясняется тем, что при постоянном давлении часть подводимой энергии расходуется на совершение силой давления газа работы при расширении. Расширение жидких и твёрдых тел при нагревании при постоянном давлении значительно меньше, чем газов, поэтому для них Адиабатный процесс Адиабатным называют процесс, в ходе которого термодинамическая система не получает и не отдаёт энергию путём теплопередачи. Таким образом, при адиабатном процессе Q = 0. Применяя к этому процессу первый закон термодинамики, получим: или При адиабатном процессе изменение внутренней энергии системы происходит только за счёт совершения работы. Если внешние силы совершают работу по сжатию газа ( 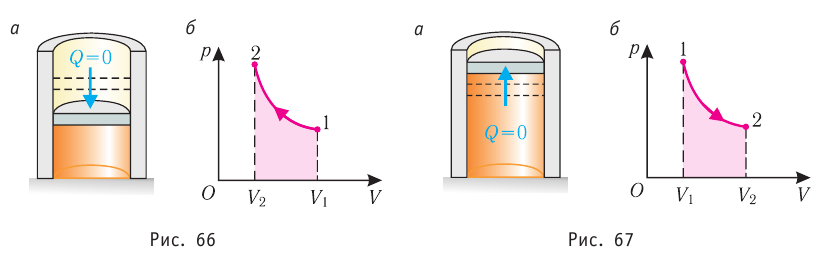 Если процесс протекает очень быстро, то теплопередача практически не сказывается. Очень нагляден опыт, иллюстрирующий уменьшение температуры газа при его адиабатном расширении. Используя насос, через отверстие в пробке будем накачивать в стеклянный сосуд воздух (рис. 68). Через некоторый промежуток времени накачивания сжатый воздух совершит работу по преодолению силы трения, с которой сосуд действует на пробку, и силы атмосферного давления. Теплопередача между сосудом и окружающими телами не успевает проявиться за тот малый промежуток времени, пока пробка вылетает из сосуда. Уменьшение внутренней энергии воздуха в сосуде выражается в понижении его температуры, что приводит к конденсации водяных паров, т. е. к образованию тумана. 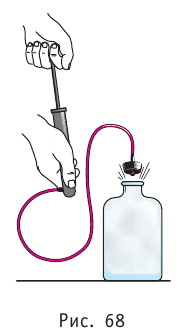 В качестве примера адиабатного процесса можно привести охлаждение воздуха в атмосфере. Нагретый возле поверхности Земли воздух при быстром подъёме в верхние слои атмосферы расширяется почти адиабатно и при этом резко охлаждается. Водяной пар в нём конденсируется в маленькие капли воды и кристаллики льда, образуя облака. Близкий к адиабатному процесс используют в двигателях внутреннего сгорания. Обратимый адиабатный процесс относят к изопроцессам, так как он характеризуется постоянством функции состояния, называемой энтропией. В отличие от остальных изопроцессов при обратимом адиабатном процессе происходят изменения давления, объёма и температуры. График адиабатного процесса в координатах (р, V) похож на график изотермического процесса (рис. 69). Однако одному и тому же изменению объёма Это объясняется тем, что в случае адиабатного расширения давление 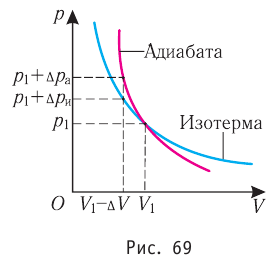 1. Приращение внутренней энергии термодинамической системы при переходе из одного состояния в другое равно алгебраической сумме работы, совершённой внешними силами, и количества теплоты, полученного или отданного системой при взаимодействии с внешними телами: 2. Количество теплоты, полученное или отданное термодинамической системой при взаимодействии с внешними телами при её переходе из одного состояния в другое, идёт на приращение внутренней энергии системы и на работу, которую система совершает при расширении: 3. При изохорном процессе всё передаваемое системе количество теплоты идёт на увеличение её внутренней энергии: 4. При изотермическом процессе работа расширения или сжатия идеального газа сопровождается теплопередачей между газом и термостатом: A=Q. 5. При изобарном процессе переданное идеальному газу количество теплоты частично расходуется на увеличение внутренней энергии газа и частично идёт на совершение работы газом при его расширении: 6. При адиабатном процессе приращение внутренней энергии газа равно работе, которую совершает сила давления газа, взятой с противоположным знаком: Пример №1 Идеальный газ, масса которого постоянна, переводят из состояния / в состояние 3 двумя различными способами: 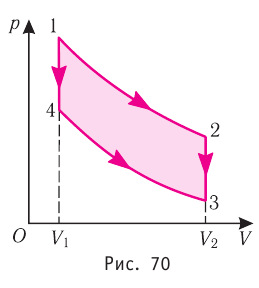 Решение, а) Так как начальное и конечное состояния для обоих переходов одинаковы, то будут одинаковы и приращения внутренней энергии: б) Из рисунка 70 видно, что площадь фигуры, ограниченной осью OV, изотермой и изохорами, проходящими через точки 3 и 4, меньше площади фигуры, ограниченной осью ОV, изотермой и изохорами, проходящими через точки 1 и 2. Следовательно, в процессе перехода в) Из первого закона термодинамики следует: Поскольку приращения внутренней энергии в обоих случаях одинаковы, а совершённая силой давления газа работа больше при переходе Ответ: а) Пример №2 Идеальный одноатомный газ, давление которого Дано: р = 2,0 • р =const Решение. Приращение внутренней энергии идеального одноатомного газа 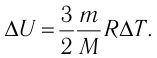 При изобарном расширении идеального газа изменение его температуры При изобарном расширении идеального газа изменение его температуры 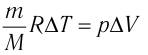 (см. пример решения задачи после § 9). Тогда (см. пример решения задачи после § 9). Тогда 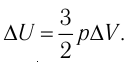 Согласно первому закону термодинамики для изобарного процесса Согласно первому закону термодинамики для изобарного процесса Отсюда 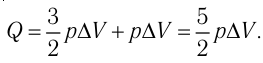 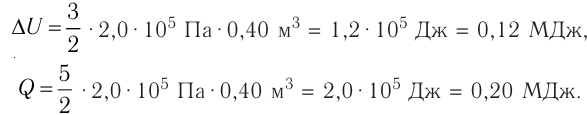 Ответ: Пример №3 В сосуд налита вода массой 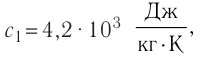 льда — льда —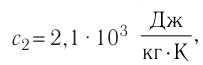 удельная теплота плавления льда удельная теплота плавления льда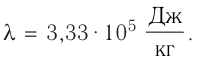 Дано 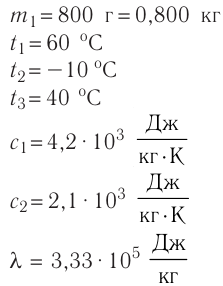 Решение. Если пренебречь потерями энергии в окружающую среду, то термодинамическая система «сосуд—вода—лёд» является изолированной. Поэтому учитываем только обмен энергией между входящими в систему телами при теплопередаче. Рассмотрим тепловые процессы, происходящие в системе: 1) нагревание льда от температуры массой Отсюда масса льда 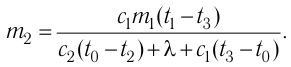 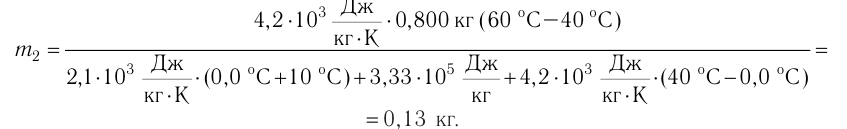 Ответ: |
