реферат по физике. Реферат по физике на тему "Изучение равновесных и квазиравновесных термодинамических процессов и экспериментальное определение показателя адиабаты воздуха "
 Скачать 1.27 Mb. Скачать 1.27 Mb.
|
|
Что называется степенями свободы молекулы и чему равно их число для одно-, двух- и трехатомных молекул? Назовите известные вам газы с одно-, двух- и трехатомными молекулами. Запишите химический состав воздуха в процентном отношении. Из каких молекул состоят газы, входящие в состав воздуха? В механике введилось понятие числа степеней свободы: это число независимых переменных (координат), которые полностью определяют положение системы в пространстве. В некоторых задачах молекулу одноатомного газа (рис. 1, а) рассматривают как материальную точку, которой задают три степени свободы поступательного движения. При этом не учитывается энергия вращательного движения. В механике молекула двухатомного газа в первом приближении считается совокупностью двух материальных точек, которые жестко связанны недеформируемой связью (рис. 1, б). Данная система кроме трех степеней свободы поступательного движения имеет еще две степени свободы вращательного движения. Вращение вокруг третьей оси, проходящей через оба атома, лишено смысла. Значит, у двухатомного газа пять степеней свободы (i = 5). У трехатомной (рис. 1, в) и многоатомной нелинейной молекулы шесть степеней свободы: три поступательных и три вращательных. Естественно считать, что жесткой связи между атомами не существует. Поэтому необходимо учитывать для реальных молекул также степени свободы колебательного движения. Рис.1 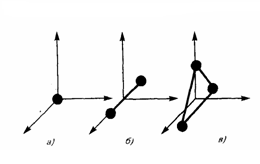 При любом числе степеней свободы данной молекулы три степени свободы всегда поступательные. Ни одна из поступательных степеней свободы не имеет преимущества перед другими, значит на каждую из них приходится в среднем одинаковая энергия, равная 1/3 значения <ε0> (энергия поступательного движения молекул): В статистической физике выводится закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для статистической системы, которая находится в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень свободы — в среднем энергия, равная kT. Колебательная степень обладает вдвое большей энергией, т.к. на нее приходится как кинетическая энергия (как в случае поступательного и вращательного движений), так и потенциальная, причем средние значения потенциальной и кинетической и энергии одинаковы. Значит, средняя энергия молекулы где i — сумма числа поступательных, числа вращательных в удвоенного числа колебательных степеней свободы молекулы: i=iпост+iвращ+2iколеб В классической теории рассматривают молекулы с жесткой связью между атомами; для них i совпадает с числом степеней свободы молекулы. Так как в идеальном газе взаимная потенциальная энергия взаимодействия молекул равна нулю (молекулы между собой не взаимодействуют), то внутренняя энергия для одного моля газа, будет равна сумме кинетических энергий NA молекул: Внутренняя энергия для произвольной массы m газа. где М — молярная масса, ν — количество вещества. Число степеней свободы тела - это сколько координат надо знать, чтобы отнгозначно описать его движение. Например, для материальной точки (имеющей нулевой размер) достаточно знать три параметра - по осям коголрдинат. В молекулярно-кинетической теории газов, помимо трех поступательных степеней свободы, есть и вращательные, число которых зависит от строения молекулы газа. Например, для кислорода или азота (молекула из двух атомов) надо рассматривать вращение вокруг двух осей (потому что вокруг третьей - это вдоль молекулы, и там нет изменения положения никакого). Для более сложных, например, аммиак, появляются все три дополнительные вращательные степени свободы. Поэтому и энергия молекул должна считаться как, например, 5/2 kT для кислорода или 3kT для аммиака, потому как полное число степеней свободы 5 и 6, соответственно. А вот гелий или неон - одноатомные газы, и для них только 3/2kT, посколку нет вращательных степеней свободы. Сте́пени свобо́ды — характеристики движения механической системы. Число степеней свободы определяет минимальное количество независимых переменных (обобщённых координат), необходимых для полного описания движения механической системы. Внутренняя энергияU - энергия хаотического (теплового) движения микрочастиц системы (молекул, атомов, электронов, ядер и т.д.) и энергия взаимодействия этих частиц. К внутренней энергии не относится кинетическая энергия движения системы как целого и потенциальная энергия системы во внешних полях.Внутренняя энергия -однозначная функция термодинамического состояния системы, т.е. в каждом состоянии система обладает вполне определенной (единственной) энергией. Внутренняя энергия не зависит от того, как система пришла в данное состояние: при переходе из состояния (1) в состояние (2) изменение внутренней энергии DU определяется только разностью значений внутренней энергии этих состояний DU = U1 - U2 и не зависит от пути перехода. Число степеней свободы системыi - это число независимых переменных (координат), полностью определяющих положение системы в пространстве: - Одноатомная молекула идеального газа имеет три степени свободы поступательного движения, т.е. i=3. - Двухатомная молекула идеального газа имеет три степени поступательного движения и две степени свободы вращательного движения, т.е. i=5. - Трехатомная молекула (и вообще нелинейная многоатомная молекула) идеального газа имеет три степени поступательного движения и три степени вращательного движения, т.е. i=6. - Для реальных молекул следует учитывать также степени свободы колебательного движения. - Независимо от числа степеней свободы молекул три степени свободы всегда поступательные; ни одна из поступательных степеней свободы не имеет преимущества перед остальными. Закон Больцмана о равномерном распределении энергии по степеням свободы молекул: для системы, находящейся в состоянии термодинамического равновесия, на каждую поступательную и вращательную степени свободы приходится в среднем кинетическая энергия, равная kT/2, а на каждую колебательную степень - в среднем энергия, равная kT (на колебательную степень свободы приходится не только кинетическая энергия, но и потенциальная, причем средние значения кинетической и потенциальной энергий одинаковы). Таким образом, средняя энергия молекулыЕ> = ikT/2, где i - сумма числа поступательных iпост, числа вращательных iвращ и удвоенного числа колебательных iколеб степеней свободы молекулы i = iпост + iвращ + 2iколеб. Для идеального газа i совпадает с числом степеней свободы молекулы. Внутренняя энергия 1 моль идеального газа равна сумме кинетических энергий NA молекул Um = ikTNA = iRT/2, (1a) и изменение внутренней энергии 1 моль идеального газа dUm =(iR/2)dT (1b) (молекулы между собой не взаимодействуют и поэтому взаимная потенциальная энергия молекул газа равна нулю). Внутренняя энергия произвольной массы m идеального газа U = (m/M)(iRT/2)=n(iRT/2), где М - молярная масса (масса одного моля), n = m/M - количество вещества. Таблица химического состава сухого воздуха, в %. 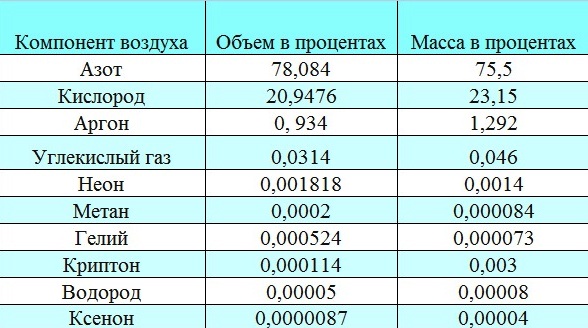  Дайте определение теплоемкости, удельной теплоемкости и молярной теплоемкости газа. В каких единицах их измеряют в СИ Теплоёмкость тела (обычно обозначается латинской буквой C) — физическая величина, определяющая отношение бесконечно малого количества теплоты δQ, полученного телом, к соответствующему приращению его температуры δT: 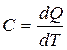 Единица измерения теплоёмкости в СИ — Дж/К. Теплоемкость тела зависит только от его химического состава, массы, вида термодинамического процесса, в широком интервале температур – от температуры. Понятие теплоёмкости определено как для веществ в различных агрегатных состояниях (твёрдых тел, жидкостей, газов), так и для ансамблей частиц и квазичастиц (в физике металлов, например, говорят о теплоёмкости электронного газа). Удельной теплоемкостью вещества называется физическая величина, численно равная количеству энергии в форме теплоты, которое надо сообщить единице массы этого вещества для увеличения его температуры на 1 Кельвин (т.е. это теплоёмкость, отнесённая к единице массы вещества): В общем случае удельная теплоемкость зависит от рода вещества и от вида термодинамического процесса, в котором телу сообщается количество теплоты. Удельные теплоёмкости многих веществ приведены в справочниках (обычно для процесса при постоянном давлении). К примеру, удельная теплоёмкость жидкой воды при нормальных условиях — 4200 Дж/(кг·К); льда – 2100 Дж/(кг·К). Количество теплоты, поглощённой телом при изменении его состояния, зависит не только от начального и конечного состояний (в частности, от их температуры), но и от способа, которым был осуществлен процесс перехода между ними. Поэтому для газов различают два вида теплоемкостей: если газ нагревают, сохраняя его объем постоянным (изохорно), говорят об удельной теплоемкости газа при постоянном объеме cV; если же газ нагревают, сохраняя постоянным его давление (изобарно), то говорят об удельной теплоемкости газа при постоянном давлении сР. У жидкостей и твёрдых тел разница между Ср и Cv сравнительно мала. Часто пользуются молярной теплоемкостью Сμ, которая, в отличие от удельной теплоемкости, отнесена не к единице массы (1 килограмму), а к массе одного моля вещества. Очевидно, что Cμ = mc, Дж/(моль×К) Для газов молярную теплоемкость, рассчитанную при постоянном давлении, обозначают СР, а рассчитанную при постоянном объеме – СV. Следовательно, СР = m×cP, CV = m×cV. Когда нагревание газа происходит при постоянном объеме, газ не совершает механической работы и все сообщаемое газу тепло идет только на увеличение его внутренней энергии DU, т.е.: DQ = m×cV×DT = DU. Если же нагревание газа происходит при постоянном давлении и, следовательно, объем газа увеличивается, то сообщаемое газу тепло DQ идет как на увеличение его внутренней энергии DU, так и на совершение газом работы DA над внешними телами, т.е. DQ = m×cP×DT = DU + DA. Из сопоставления формул следует, что cP > cV, т.е. удельная теплоемкость газа при постоянном давлении больше удельной теплоемкости того же газа при постоянном объеме. При этом, согласно уравнению Майера: CP = CV + R. В данной работе требуется определить не абсолютные значения теплоемкостей газа, а их отношение, называемое коэффициентом Пуассона: 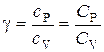 . .Теоретическое вычисление теплоемкости, в частности её зависимости от температуры тела, не может быть осуществлено с помощью чисто термодинамических методов и требует применения методов статистической физики. Чему равны молярные теплоемкости идеального газа при изобарическом, изохорическом, изотермическом и адиабатическом процессах? Каким соотношением связаны между собой молярные теплоемкости идеального газа при изобарическом и изохорическом процессах? Первый закон термодинамики есть закон сохранения энергии в применении его к термодинамическим процессам. Можно дать несколько, по существу равноценных, формулировок этого закона: а) общая энергия изолированной системы остается постоянной независимо от каких бы то ни было изменений, происходящих в этой системе; б) изменение внутренней энергии системы (∆U) равно разности между количеством сообщенной системе теплоты q и количеством работы А, совершенной системой. Математическое выражение первого закона термодинамики будет иметь вид: ∆U = q - A (2.1) q - считается положительной, если теплота поглощается системой, и отрицательной, если теплота выделяется [2]. Из первого закона термодинамики вытекает ряд следствий, имеющих большое значение для физической химии и решения различных технологических задач. Мы ограничимся применением первого закона термодинамики только для идеальных газов и рассмотрим важнейшие процессы: изохорический, изобарический, изотермический и адиабатический. Изохорический процесс Изохорический процесс протекает при постоянном объеме, поэтому система никакой работы не совершает. В этом случае вся теплота расходуется на увеличение внутренней энергии системы. Если V - соnst, то A=0, тогда qV = ∆U При изохорическом процессе количество теплоты, получаемое системой, можно вычислить по уравнениям: qV |
