фазовые переходы. Копать_Владислав. Реферат По теме Фазовые переходы

• Название: Реферат По теме Фазовые переходы
• Анкор: фазовые переходы
• Дата: 20.05.2022
• Размер: 122.74 Kb.
• Имя файла: Копать_Владислав.docx
• Тип: Реферат; #539605

Белорусский государственный университет 

Факультет радиофизики и компьютерных технологий


Реферат

По теме: «Фазовые переходы»

                                                                            

   Выполнил: 

студент 1 курса 4 группы

 Копать Владислав

Преподаватель:

Литвинович Глеб Святославович 
Содержание
1. Значение фазового перехода

2. Классификация фазовых переходов

3. Фазовые переходы первого рода

4. Квантовый фазовый переход

5. Фазовые переходы второго рода

6. Равновесие фаз

Список литературы


1. Значение фазового перехода
Фазовый переход (фазовое превращение) в термодинамике — переход вещества из одной термодинамической фазы в другую при изменении внешних условий. С точки зрения движения системы по фазовой диаграмме при изменении её интенсивных параметров (температуры, давления и т. п.), фазовый переход происходит, когда система пересекает линию, разделяющую две фазы. Поскольку разные термодинамические фазы описываются различными уравнениями состояния, всегда можно найти величину, которая скачкообразно меняется при фазовом переходе.

Поскольку разделение на термодинамические фазы — более мелкая классификация состояний, чем разделение по агрегатным состояниям вещества, то далеко не каждый фазовый переход сопровождается сменой агрегатного состояния. Однако любая смена агрегатного состояния есть фазовый переход.

Наиболее часто рассматриваются фазовые переходы при изменении температуры, но при постоянном давлении (как правило, равном 1 атмосфере). Именно поэтому часто употребляют термины «точка» (а не линия) фазового перехода, температура плавления и т. д. Разумеется, фазовый переход может происходить и при изменении давления, и при постоянных температуре и давлении, но и при изменении концентрации компонентов (например, появление кристалликов соли в растворе, который достиг насыщения).

2. Классификация фазовых переходов
Фазовые переходы первого рода — фазовые переходы, при которых скачком изменяются первые производные термодинамических потенциалов по интенсивным параметрам системы (температуре или давлению). Переходы первого рода реализуются как при переходе системы из одного агрегатного состояния в другое, так и в пределах одного агрегатного состояния (в отличие от фазовых переходов второго рода, которые происходят в пределах одного агрегатного состояния)

Наиболее распространённые примеры фазовых переходов первого рода:

• 
  плавление и кристаллизация
  
• 
  испарение и конденсация
  
• 
  сублимация и десублимация
  

Фазовые переходы второго рода — фазовые переходы, при которых вторые производные термодинамических потенциалов по давлению и температуре изменяются скачкообразно, тогда, как их первые производные изменяются постепенно. Отсюда следует, в частности, что энергия и объём вещества при фазовом переходе второго рода не изменяются, но изменяются его теплоёмкость, сжимаемость, различные восприимчивости и т. д. Фазовые переходы второго рода происходят в тех случаях, когда меняется симметрия строения вещества (симметрия может полностью исчезнуть или понизиться). Описание фазового перехода второго рода как следствие изменения симметрии даётся теорией Ландау. В настоящее время принято говорить не об изменении симметрии, но о появлении в точке перехода параметра порядка, равного нулю в менее упорядоченной фазе и изменяющегося от нуля (в точке перехода) до ненулевых значений в более упорядоченной фазе.

Наиболее распространённые примеры фазовых переходов второго рода:

• 
  прохождение системы через критическую точку
  
• 
  переход парамагнетик-ферромагнетик или парамагнетик -антиферромагнетик (параметр порядка — намагниченность)
  
• 
  переход металлов и сплавов в состояние сверхпроводимости (параметр порядка — плотность сверхпроводящего конденсата)
  
• 
  переход жидкого гелия в сверхтекучее состояние (п. п. — плотность сверхтекучей компоненты)
  
• 
  переход аморфных материалов в стеклообразное состояние
  

Современная физика исследует также системы, обладающие фазовыми переходами третьего или более высокого рода.

В последнее время широкое распространение получило понятие квантовый фазовый переход, то есть фазовый переход, управляемый не классическими тепловыми флуктуациями, а квантовыми, которые существуют даже при абсолютном нуле температур, где классический фазовый переход не может реализоваться вследствие теоремы Нернста.
3. Фазовые переходы первого рода
Плавление — это процесс превращения вещества из твёрдого состояния в жидкое.

Наблюдения показывают, что если измельчённый лёд, имеющий, например, температуру –10 °С, оставить в тёплой комнате, то его температура будет повышаться. При 0 °С лёд начнет таять, а температура при этом не будет изменяться до тех пор, пока весь лёд не превратится в жидкость. После этого температура образовавшейся изо льда воды будет повышаться.

Это означает, что кристаллические тела, к которым относится и лед, плавятся при определённой температуре, которую называют температурой плавления. Важно, что во время процесса плавления температура кристаллического вещества и образовавшейся в процессе его плавления жидкости остаётся неизменной.

В описанном выше опыте лёд получал некоторое количество теплоты, его внутренняя энергия увеличивалась за счёт увеличения средней кинетической энергии движения молекул. Затем лёд плавился, его температура при этом не менялась, хотя лёд получал некоторое количество теплоты. Следовательно, его внутренняя энергия увеличивалась, но не за счёт кинетической, а за счёт потенциальной энергии взаимодействия молекул. Получаемая извне энергия расходуется на разрушение кристаллической решетки. Подобным образом происходит плавление любого кристаллического тела.

Аморфные тела не имеют определённой температуры плавления. При повышении температуры они постепенно размягчаются, пока не превратятся в жидкость.

Кристаллизация — это процесс перехода вещества из жидкого состояния в твёрдое состояние. Охлаждаясь, жидкость будет отдавать некоторое количество теплоты окружающему воздуху. При этом будет уменьшаться её внутренняя энергия за счёт уменьшения средней кинетической энергии его молекул. При определённой температуре начнётся процесс кристаллизации, во время этого процесса температура вещества не будет изменяться, пока всё вещество не перейдет в твёрдое состояние. Этот переход сопровождается выделением определённого количества теплоты и соответственно уменьшением внутренней энергии вещества за счёт уменьшения потенциальной энергии взаимодействия его молекул.

Таким образом, переход вещества из жидкого состояния в твёрдое состояние происходит при определённой температуре, называемой температурой кристаллизации. Эта температура остаётся неизменной в течение всего процесса плавления. Она равна температуре плавления этого вещества.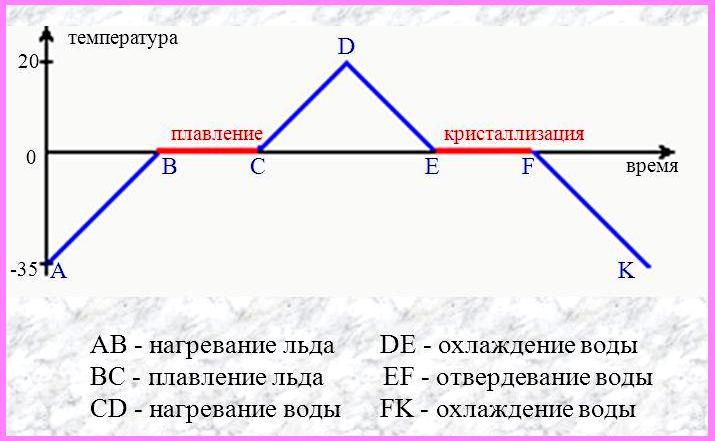



 

На рисунке приведён график зависимости температуры твёрдого кристаллического вещества от времени в процессе его нагревания от комнатной температуры до температуры плавления, плавления, нагревания вещества в жидком состоянии, охлаждения жидкого вещества, кристаллизации и последующего охлаждения вещества в твёрдом состоянии.

Испаре́ние— процесс фазового перехода вещества из жидкого состояния в парообразное или газообразное, происходящий на поверхности вещества. При испарении с поверхности жидкости или твёрдого тела вылетают (отрываются) частицы (молекулы, атомы), при этом их кинетическая энергия должна быть достаточна для совершения работы, необходимой для преодоления сил притяжения со стороны других молекул жидкости. Во время процесса испарение, энергия, извлеченная из испаряемой жидкости, снижает температуру жидкости, что приводит к испарительному охлаждению.

В среднем только часть молекул жидкости имеет достаточно тепловой энергии, чтобы выйти из жидкости. Процесс испарения является обратным процессу конденсации (переход из парообразного состояния в жидкое). Испарение будет продолжаться до тех пор, пока не будет достигнуто равновесие, во время которого испарение жидкости равно её конденсации. В замкнутом пространстве жидкость будет испаряться до тех пор, пока окружающий воздух не станет насыщенным.

Конденса́ция паров (лат. condense «накопляю, уплотняю, сгущаю») — переход вещества в жидкое или твёрдое^[1] состояние из парообразного (обратный последнему процессу называется сублимация). Максимальная температура, ниже которой происходит конденсация, называется критической. Пар, из которого может происходить конденсация, бывает насыщенным или ненасыщенным.

Конденсация имеет место во многих теплообменных аппаратах (например, в мазутоподогревателях на ТЭС), в опреснительных установках, технологических аппаратах (перегонные аппараты). Важнейшее применение на ТЭС — конденсаторы паровых турбин. В них конденсация происходит на охлаждаемых водой трубах. Для повышения КПД термодинамического цикла ТЭС важно снижать температуру конденсации (за счёт понижения давления), и обычно она близка к температуре охлаждающей воды (до 25—30 °C).

Сублима́ция (от лат. sublimo «возносить»), возго́нка — переход вещества из твёрдого состояния сразу в парообразное, минуя стадию плавления (перехода в жидкое состояние) и кипения. Поскольку при возгонке изменяется удельный объём вещества и поглощается энергия (теплота сублимации), возгонка является фазовым переходом первого рода.

Десублима́ция (Депози́ция) — физический процесс перехода вещества из газообразного состояния в твёрдое, минуя жидкое. При десублимации высвобождается энергия. Десублимация является экзотермическим фазовым переходом. Обратным процессом является возгонка (сублимация). Десублимация осуществляется на твёрдые поверхности или происходит в объёме газовой фазы с выделением твердого вещества в виде частиц аэрозоля.

При десублимации (процесс самоорганизации) возникают ван-дер-ваальсовы связи между отдельными молекулами вещества с выделением энергии, которую отводят от десублимата непосредственным контактом его с охлаждаемой твёрдой поверхностью, взаимодействуя с вводимым дополнительно хладагентом, испарением жидкости, добавляемой в газовую смесь, её расширением.

Примером десублимации является появление ледяных узоров на оконных стёклах в зимнее время и такие атмосферные явления, как иней и изморозь.
5. Квантовый фазовый переход

Чтобы понять квантовые фазовые переходы, полезно сравнить их с классическими фазовыми переходами (КПН) (также называемыми тепловыми фазовыми переходами). CPT описывает излом в термодинамических свойствах системы. Это сигнализирует о реорганизации частиц; Типичный пример - замерзание воды, описывающее переход от жидкости к твердому телу. Классические фазовые переходы вызваны конкуренцией между энергией системы и энтропией.его тепловых колебаний. Классическая система не имеет энтропии при нулевой температуре, и поэтому фазовый переход не может происходить. Их порядок определяется первой разрывной производной термодинамического потенциала. Фазовый переход от воды к льду, например, включает скрытую теплоту (разрыв внутренней энергии ) и имеет первый род. Фазовый переход от ферромагнетика к парамагнетику непрерывен и имеет второй род. (См. Фазовый переход для классификации фазовых переходов Эренфеста по производной свободной энергии, разрывной при переходе). Эти непрерывные переходы из упорядоченной фазы в неупорядоченную описываются параметром порядка, который равен нулю в неупорядоченной фазе и отличен от нуля в упорядоченной фазе. Для вышеупомянутого ферромагнитного перехода параметр порядка будет представлять полную намагниченность системы.

Хотя термодинамическое среднее параметра порядка равно нулю в неупорядоченном состоянии, его флуктуации могут отличаться от нуля и становиться дальнодействующими вблизи критической точки, где их типичный масштаб длины ξ (длина корреляции) и типичный масштаб времени затухания флуктуаций τ _c (время корреляции) расходятся: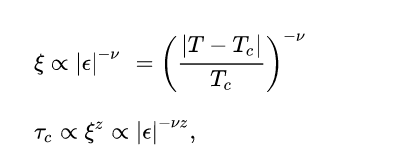



Где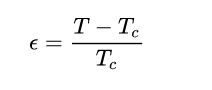



определяется как относительное отклонение от критической температуры T _c . Мы называем ν критическим показателем ( корреляционной длины ), а z - динамическим критическим показателем . Критическое поведение фазовых переходов при ненулевой температуре полностью описывается классической термодинамикой ; квантовая механика не играет никакой роли, даже если фактические фазы требуют квантово-механического описания (например, сверхпроводимости ).

6. Фазовые переходы второго рода
Изменение симметрии

Фазовые переходы второго рода сопровождаются изменением симметрии вещества. Изменение симметрии может быть связано со смещением атомов определённого типа в кристаллической решётке, либо с изменением упорядоченности вещества.

В большинстве случаев, фаза, обладающая большей симметрией (т. е. включающей в себя все симметрии другой фазы), соответствует более высоким температурам, но существуют и исключения. Например, при переходе через нижнюю точку Кюри в сегнетовой соли, фаза, соответствующая меньшей температуре, обладает ромбической симметрией, в то время как фаза, соответствующая большей температуре, обладает моноклинной симметрией.

Для количественной характеристики симметрии при фазовом переходе второго рода вводится параметр порядка, принимающий отличные от нуля значения в фазе с большей симметрией, и тождественно равный нулю в неупорядоченной фазе.

Теоретическое описание фазовых переходов второго рода

Теория Ландау

Теория среднего поля – самый первый и простейший способ теоретического описания критических явлений. Для этого производится линеаризация много частичного гамильтониана взаимодействия, то есть фактически, он заменяется на одно частичный гамильтониан с некоторым эффективным самосогласованным полем. Таким образом, мы переходим от близкодействия к дальнодействию, то есть к взаимодействию с формально бесконечным радиусом. Также мы пренебрегаем корреляционными эффектами.

Применение теории среднего поля для описания фазовых переходов фактически эквивалентно применению теории Ландау, то есть разложению функционала свободной энергии по степеням параметра порядка около критической точки.

При описании фазовых переходов, эффективное поле обычно принимается пропорциональным параметру порядка. Как правило, множителем пропорциональности является средняя энергия взаимодействия частиц системы. Так, в магнетике рассматривается действие на отдельный электронный спин локального магнитного поля, создаваемое соседними спинами.

Критические показатели для магнетика в теории Ландау:













Для других систем – антиферромагнетика, бинарного сплава и системы жидкость-пар теория среднего поля даёт те же критические показатели.

Критические показатели, полученные в теории среднего, поля плохо согласуются с экспериментальными значениями. Но она предсказывает полную универсальность показателей, то есть их независимость от деталей теории.

Основным недостатком теории является то, что она неприменима в тех случаях, когда существенными становятся флуктуации параметра порядка, то есть непосредственно в окрестности точки фазового перехода: Теория Ландау справедлива до тех пор, пока флуктуации в объеме с линейными размерами порядка радиуса корреляции малы по сравнению с равновесным значением параметра порядка. В противном случае термодинамический подход неприменим. Для самих точек фазового перехода теория даёт завышенные показания, а предсказываемые ей критические показатели отличаются от экспериментальных значений. Кроме того, критические показатели, согласно теории среднего поля, не зависят от размерностей пространства и параметра порядка. Для систем с размерностями d=1, d=2 теория среднего поля вообще не применима.

• 
  Примеры фазовых переходов второго рода
  
• 
  переход парамагнетик-ферромагнетик или парамагнетик -антиферромагнетик (параметр порядка — намагниченность),
  
• 
  переход металлов и сплавов в состояние сверхпроводимости (параметр порядка — плотность сверхпроводящего конденсата),
  
• 
  переход жидкого гелия в сверхтекучее состояние (п.п. — плотность сверхтекучей компоненты),
  
• 
  переход аморфных материалов в стеклообразное состояние.
  

7. Равновесие фаз
Равновесие фаз в термодинамике — состояние, при котором фазы в термодинамической системе находятся в состоянии теплового, механического и химического равновесия.

Типы фазовых равновесий:

Тепловое равновесие означает, что все фазы вещества в системе имеют одинаковую температуру.

Механическое равновесие означает равенство давлений по разные стороны границы раздела соприкасающихся фаз. Строго говоря, в реальных системах эти давления равны лишь приближенно, разность давлений создается поверхностным натяжением.

Химическое равновесие выражается в равенстве химических потенциалов всех фаз вещества.

Условие равновесия фаз

Рассмотрим химически однородную систему (состоящую из частиц одного типа). Пусть в этой системе имеется граница раздела между фазами 1 и 2. Как было указано выше, для равновесия фаз требуется равенство температур и давлений на границе раздела фаз. Что состояние термодинамического равновесия в системе с постоянными температурой и давлением соответствует точке минимума потенциала Гиббса.

Потенциал Гиббса такой системы будет равен
,
где и — химические потенциалы, а и — числа частиц в первой и второй фазах соответственно.

При этом сумма (полное число частиц в системе) меняться не может, поэтому можно записать

.
Предположим, что , для определенности, . Тогда, очевидно, минимум потенциала Гиббса достигается при (все вещество перешло в первую фазу).

Таким образом, равновесие фаз возможно только в том случае, когда химические потенциалы этих фаз по разные стороны границы раздела равны:

.

Уравнение Клаперона-Клаузиса

Из условия равновесия фаз можно получить зависимость давления в равновесной системе от температуры. Если говорить о равновесии жидкость — пар, то под давлением понимают давление насыщенных паров, а зависимость называется кривой испарения.

Из условия равенства химических потенциалов следует условие равенства удельных термодинамических потенциалов : , где
,
потенциал Гиббса i-й фазы, — её масса.

Отсюда:

,

а значит,
,
где и — удельные объем и энтропия фаз. Отсюда следует, что
,
и окончательно
,
где — удельная теплота фазового перехода (например, удельная теплота плавления или удельная теплота испарения).

Последнее уравнение называется уравнением Клапейрона — Клаузиуса.

Правило фаз Гиббса

термодинамическом равновесии, число фаз не может превышать числа компонентов, увеличенного на 2 ; установлено Дж. У. Гиббсом в 1873—76.

Рассмотрим теперь систему, вообще говоря, химически неоднородную (состоящую из нескольких веществ). Пусть 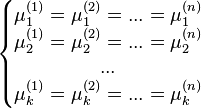— число компонентов (веществ) в системе, а — число фаз. Условие равновесия фаз для такой системы можно записать в виде системы из уравнений:

Здесь — химический потенциал для i-го компонента в j-й фазе. Он однозначно определяется давлением, температурой и концентрацией каждого компонента в фазе. Концентрации компонентов не независимы (их сумма равна 1). Поэтому рассматриваемая система уравнений содержит неизвестных ( — концентрации компонентов в фазах, плюс температура и давление).

Система разрешима, вообще говоря, если число уравнений не превышает числа неизвестных (система, не удовлетворяющая этому условию, также может быть разрешима, однако это исключительный случай, с которым в физике можно не считаться). Поэтому
,
отсюда
,
то есть число фаз в равновесной системе может превышать число компонентов не более, чем на два.

Последнее неравенство называется правилом фаз Гиббса. В частном случае для однокомпонентной (химически однородной системы) оно превращается в условие

.

Список литературы

1. 
   Арцимович Л.А. Элементарная физика плазмы, М.: ИНФРА-М, 2001.-597с.
   
2. 
   Зельдович Б.И., Мышкис А.Д. Элементы математической физики. — М.: Просвещение, 2001. — 352с.
   
3. 
   Кибец И. Н., Кибец В.И. Физика. Справочник. - Харьков: Фолио ; Ростов н/Д : Феникс, 2003.-587с.
   
4. 
   Рузавин Г.И. Концепции современного естествознания. М.: ИНФРА-М, 2003.-722с.
   
5. 
   Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика: Учеб. пособие для студентов втузов. — М.: Наука, 2002. — 432с.
   
6. 
   Франк-Каменецкий Д.А. Плазма – четвёртое состояние вещества, М, Просвещение, 2001.- 679с.
   
7. 
   Интернет https://ru.wikipedia.org