ТОАТ КУРСОВОЙ. Реферат Построение функциональной схемы сау эп
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
8.Исследование САУ ЭП с П-регулятором на модели Структурная схема САУ ЭП с П-регулятором приведена на рисунке 8.1. На этой схеме блок «ТП-ДПТ-Р-Н» включает в себя все элементы структурной схемы, относящиеся к электроприводу как объекту управления. 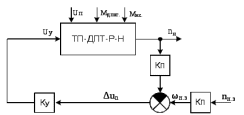 Рисунок 8.1 Структурная схема ЭП с П-регулятором Для удобства моделирования обратная связь на приведенной схеме образована не по значению угловой скорости ωн,, а по значению частоты вращения nн., ,т.е. блок «ТП-ДПТ-Р-Н» включает в себя и преобразователь значений ωн (рад/с) в значения nн (об/мин), как и в схеме модели на рисунке 6.1 Звенья с коэффициентами передачи кн. соответствует датчикам частоты вращения nн. Значение кн можно определить, исходя из условия,что при максимальном значении nн номинальное напряжение на выходе датчика (Uп.ном) равно 5В.В частности при nн.макс=40 об./мин. имеем: 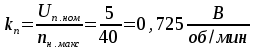 . .Звено с коэффициентом передачи (усиления) ку соответствует усилению, реализующему пропорциональный закон управления. Для упрощения структурной схемы САУ ЭП звенья с передаточным коэффициентом кп. целесообразно перенести через звено сравнения (сумматор). В полученной схеме (рисунок8.2) при моделировании можно непосредственно наблюдать и измерять отклонение Δnн выходной переменной от заданного значения nн.з..  Рисунок8.2. структурная схема САУ ЭП с П-регулятором. Схема модели САУ ЭП с П-регулятором приведена на рисунке 8.3. Исследование влияние коэффициента усиления ку(а следовательно, и коэффициента передачи разомкнутой системы к) на характер переходных процессов удобнее производить при постоянных значениях Uп.и Mн.с ,в частности, при Uп.= Uп.ном. и Mн.с= Mн.с.макс. Поэтому соответствующие входа блока «ТП-ДПТ-Р-Н» подключены непосредственно к выходам блоков SP2 и SP4. Чтобы моделируемая система по своим динамическим свойствам была близка к линейной, в ней в блоке «ТП-ДПТ-Р-Н» временно удалим блок ограничения L1 (рисунок 6.1), подключив выход блока TF1 непосредственно ко входу блока М1. Для образования в ЭП обратной связи по переменной nн в диаграмму добавлены звено сравнения S7, блок а9 («gain») c коэффициентом передачи кп (соответствующий датчику значений переменной nн) и блок SP6(«slider»), соответствующий задающему устройству. Кроме того, в модель введены блок умножения М3(«multiply») и задатчик коэффициента усиления ку блок SP7(«slider»). Использование этих двух блоков вместо одного блока «gain» с коэффициентом усиления ку позволяет изменять значение ку в любых пределах. Запустив программу на выполнение и наблюдая за переходными процессами по осциллографу, изменяя значения коэффициента ку, добиваемся такого режима работы САУ ЭП, когда в ней происходят незатухающие гармонические процессы. Система в этом режиме находится на границе устойчивости, значение коэффициента усиления ку= ку.кр..=16,2 соответствует критическому. При ку< ку.кр. колебательные процессы в системе затухают - система устойчива, при ку> ку.кр - расходятся – система не устойчива. Получим осциллограммы переходных процессов nн.(t) в системе для случаев, когда она находится на границе устойчивости (при ку= ку.кр) и когда имеет запасы устойчивости по амплитуде (β), равные 2 (при ку=8,1) и 4 (при ку=4,05). Для этого блоки М3 и SP7 заменим одним блоком «gain» с коэффициентом усиления ку и на одной диаграмме построим три схемы к модели САУ ЭП, отличающиеся значением коэффициента ку. Вид измененной модели САУ ЭП и результаты исследований nн.(t) приведены на рисунке 8.4. На этом рисунке объединенный блок «ТП-ДПТ-Р-Н» включает в себя не только блок «ТП-ДПТ-Р-Н» на рисунке8.3, но и блоки SP2 и SP4. Анализ осциллограмм показывает, что при уменьшении коэффициента ку, а следовательно, и коэффициента к, т.е. при увеличении запаса устойчивости β, колебательность переходного процесса снижается; максимальное перерегулирование и число перерегулирований N уменьшаются (при β=2 и β=4 имеем соответственно δ 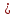 60%, N=1),время регулирования tрег.уменьшается с 0,4 до 0,2. В то же время в установившемся режиме увеличивается отклонение nн.уст. от заданного значения nн.з.= 40об/мин. А именно, при β=2 Δnн.ст.=4,5 об/мин., а при β=4 Δnн.ст.=7,5 об./мин. При β=1 в системе наблюдаются незатухающие гармонические колебания, САУ ЭП находится на границе устойчивости и неработоспособна. 60%, N=1),время регулирования tрег.уменьшается с 0,4 до 0,2. В то же время в установившемся режиме увеличивается отклонение nн.уст. от заданного значения nн.з.= 40об/мин. А именно, при β=2 Δnн.ст.=4,5 об/мин., а при β=4 Δnн.ст.=7,5 об./мин. При β=1 в системе наблюдаются незатухающие гармонические колебания, САУ ЭП находится на границе устойчивости и неработоспособна. 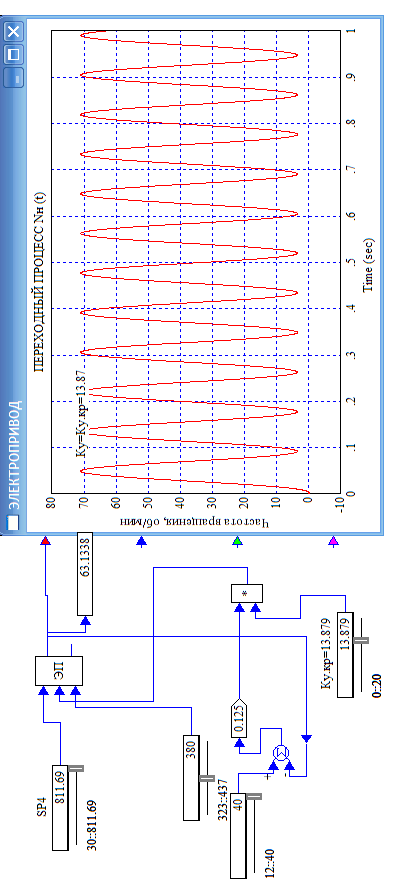 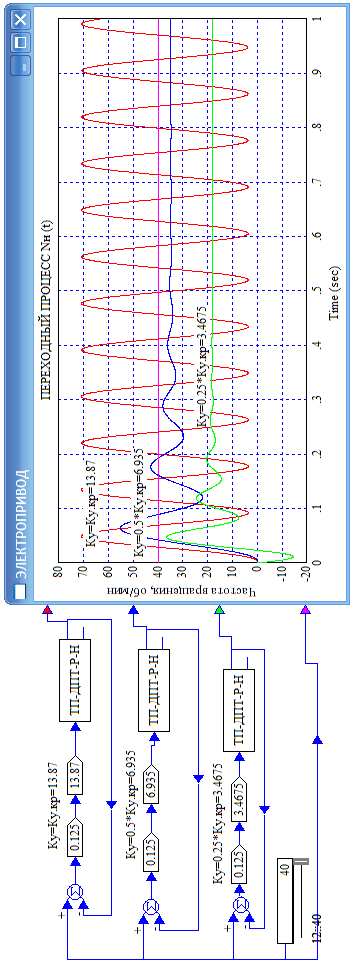 Далее проведем исследование влияния на выходную величину nн при β=2 и β=4 скачкообразных возмущений по напряжению питания Uп и по нагрузкеMн.с. Для этого на диаграмме (рисунок 8.5)разместим генераторы ступенчато изменяющихся переменных Uп и Mн.с, аналогичные генераторам диаграммы на рисунке 6.2. Построение модели САУ ЭП и осциллограммы исследований приведены на рисунке8.5. Анализ результатов исследований показывает, что при nн.з.=40 об./мин изменение возмущений Uп и Mн.с в заданных приделах не существенно сказывается на разбросе установившихся значений nн ,а именно: при β=2, nн.уст.max=36 об/мин, nн.уст.мин=34,6об/мин, разброс значения nн.уст составляет nн.уст=1,4об/мин; при β=4, nн.уст.max=32,8об/мин, nн.уст.мин=30,4об/мин, разброс Δnн.уст=2,8об/мин. В целом введение САУ с П-регулятором в сравнении с ЭП без регулятора (осциллограммы рисунка 6.2) дает определенные преимущества при действии возмущений. Так значение nн.уст меньше подвержено влиянию скачкообразных возмущений по Uп и Mн.с , переходные процессы при каждом изменении возмущения заканчиваются быстрее, Δnн.уст имеет меньший разброс значений. Тем не менее при САУ ЭП с П-регулятором отклонение фактических значений nн от заданного nн.з. в установившихся режимах составляет : при β=2, nн.ст=4 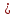 5,4об./мин, 5,4об./мин,при β=4, nн.ст=7,2 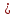 9,6об./мин, 9,6об./мин,что не удовлетворяет требованиям задания и требует дальнейшего совершенствования алгоритма управления САУ ЭП. На модели САУ ЭП с П-регулятором для разомкнутой системы получит амплитудно-фазовые характеристики (АФХ) при различных значениях запаса устойчивости β, для чего необходимо выделить все блоки замкнутого контура (т.е. цепи обратной связи) кроме звена сравнения (сумматора). Далеезапуская программу на выполнение и выделяя строку «Nyquist Response» («Характеристика Найквиста») в меню «Analyse»(«анализ») получает АФХ на комплексной плоскости [годограф комплексного коэффициента передачи W(jω)], позволяющую судить об устойчивости системы на основании критерия Найквиста. На рисунках 8.6, 8.7, 8.9 приведены АФХ САУ ЭП с П-регулятором при значениях запаса устойчивости по усилению (амплитуде) β равных: 2, 1 и 4 соответственно. При этом ку=8.1, 16.2, 4.05 соответственно. Из АФХ рисунка 8.6 видно, что при угловой скорости вращения вала нагрузки ωπ(соответствующей φ=-π) значение комплексного коэффициента передачи ККП 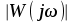 равно 0,5, что и соответствует двойному запасу по усилению(амплитуде), так как равно 0,5, что и соответствует двойному запасу по усилению(амплитуде), так как 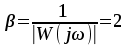 На той же модели САУ ЭП с П-регулятором получим логарифмические амплитудную и фазовую частотные характеристики [ЛАЧХ L(ω) и ЛФЧХ φ(ω)] разомкнутой системы, для чего в меню «Analyse» необходимо выделить пункт «Frequency Response» («Частотная характеристика»). Эти характеристики получим для тех же трех значений β. Характеристики представлены на рисунках 8.9,8.10 и 8.11. По ЛАЧХ и ЛФЧХ определим запасы устойчивости Lзап (по амплитуде в логарифмическом масштабе) и 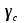 (по фазе). (по фазе).Так, при β=1 рисунок 8.9 Lзап. 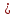 0 дБ, 0 дБ, 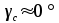 ; ;при β=2 рисунок 8.10 Lзап. 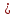 6,2 дБ, 6,2 дБ, 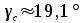 ; ;при β=4 рисунок 8.11 Lзап. 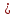 12,4 дБ, 12,4 дБ, 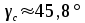 . .Проведенные исследования подтверждают ранее выводы о влиянии запасов устойчивости САУ на качество переходных процессов. С увеличением запасов устойчивости поLзап и 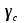 качество переходных процессов улучшается, а именно: уменьшается перерегулирование, уменьшается колебательность , уменьшается время регулирования. качество переходных процессов улучшается, а именно: уменьшается перерегулирование, уменьшается колебательность , уменьшается время регулирования.Однако в статических состояниях в САУ с П-регулятором сохраняется большое отклонение выходной величины ЭП от заданного значения. Причем, с увеличением запасов устойчивости отклонение возрастает, что ухудшает точность системы. Это не удовлетворяет требованиям задания. Поэтому необходимо дальнейшее совершенствование алгоритма управления САУ ЭП. 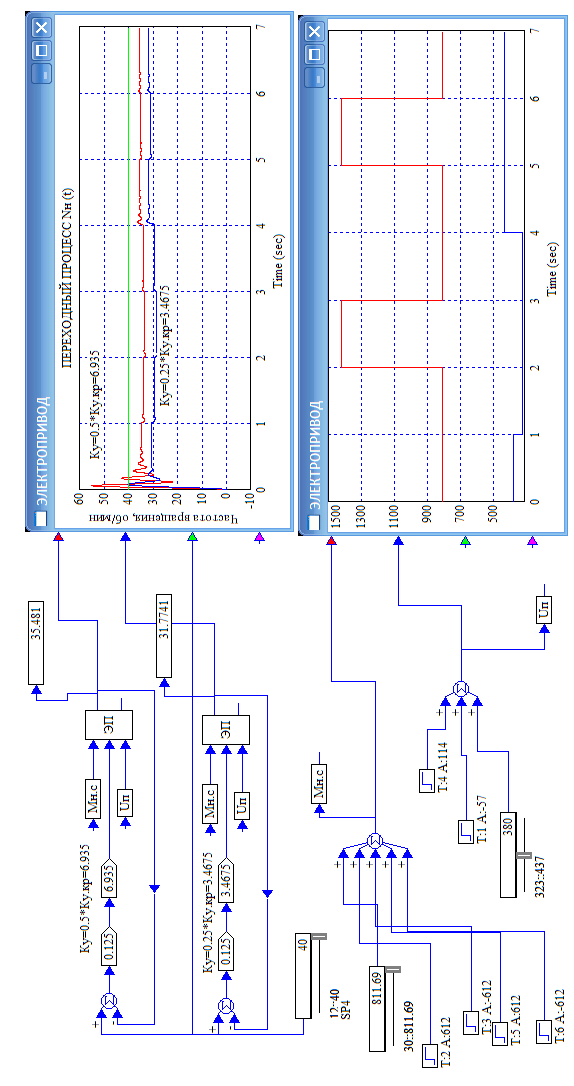 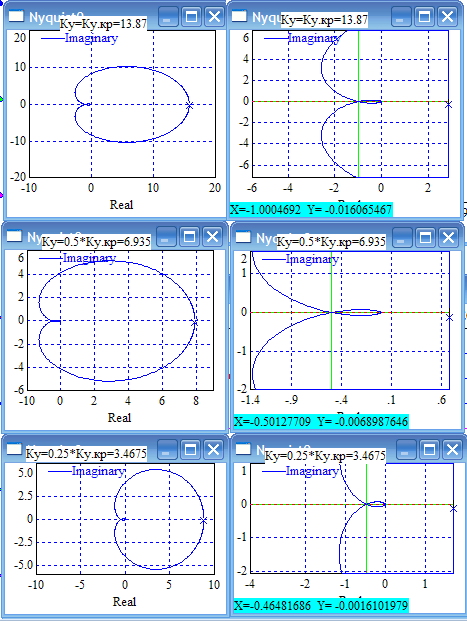 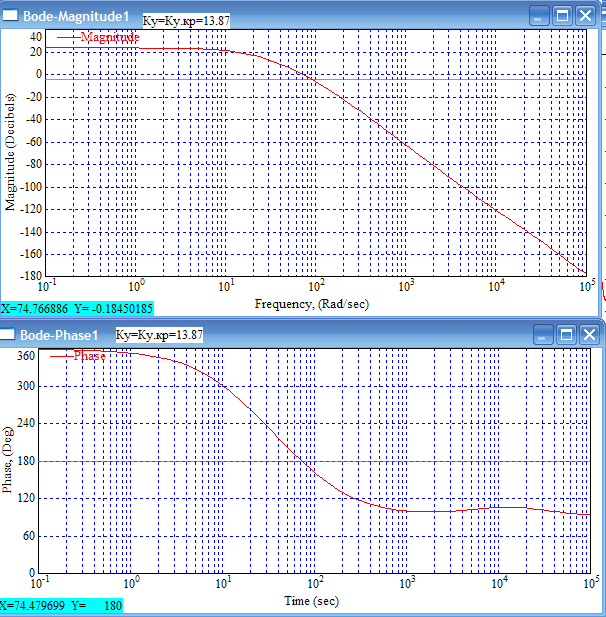 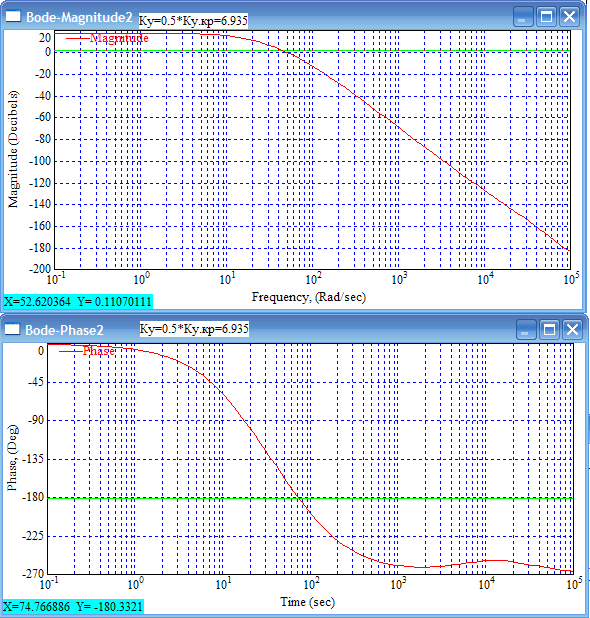 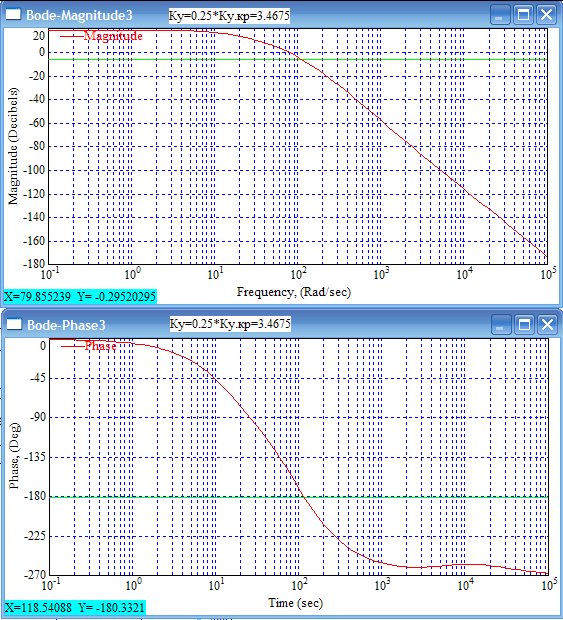 9. Построение статических САУ ЭП Если изменением коэффициента усиления усилителя ку, а следовательно и коэффициента преобразования системы к, не удается обеспечить требования к качеству управления в станционных режимах, то в САУ целесообразно использовать интегральный или пропорционально-интегральный законы управления. Результаты, реализующие такие законы управления, называются интегральными (И-регуляторами) и пропорционально-интегральными(ПИ-регуляторами). Указанные законы управления обычно реализуют путем включения в регулятор РС(регулятор скорости) интегрирующих или изодромных звеньев, имеющих передаточные функции: 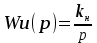 ; ;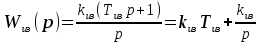 . . Струкутурная схема САУ после её приведения к одноконтурному виду может содержать на участке между точкой воздействия возмущения f и выходом y звенья с интегрирующими свойствами. В замкнутом контуре регулирования также могут иметься звенья интегрирующего типа, наличие которых обусловлено, например, интегрирующими свойствами ОУ. При использовании И- или ПИ-регуляторов число таких звеньев увеличивается. Пусть q- общее число звеньев интегрирующего типа в замкнутом контуре САУ, т. е. передаточная функция W(p) выраженная (7.3) содержит в знаменателе множитель рq. Тогда в статическом режиме для той составляющей переменной у, которая обусловлена действием возмущения f на основании (7.3) и (7.4) Применительно к данному курсовому проекту имеем, что в преобразованной одноконтурной структурной схеме САУ ЭП(рисунок 7.2) вообще отсутствуют звенья интегрирующего типа. Т.е. l=0[нет интегрирующих или изодромных звеньев в прямой цепи от f(Mн.с) до Y(ωн )] и до q=0(нет таких звеньев и в контуре главной обратной связи). В связи с этим в статическом режиме при (к=0)имеем статические ошибки слежения Δycт(уз.)[ Δ ωн.ст(ωн.з) 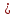 0]и статическое отклонение Δycт(f.)[ Δ ωн.ст(Mн.с.ст ) 0]и статическое отклонение Δycт(f.)[ Δ ωн.ст(Mн.с.ст )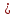 0]. Это подтверждается и результатами анализа, представленными в разделе 7(выражение7.9), и исследованиями раздела 8(рисунки 8.4 и 8.5). 0]. Это подтверждается и результатами анализа, представленными в разделе 7(выражение7.9), и исследованиями раздела 8(рисунки 8.4 и 8.5).Для получения равных нулю статической ошибки слежения Δωн.ст(ωн.з.)=0 и статического отклонения выходной величины от возмущения Δ ωн.ст(Mн.с.ст )=0 достаточно в регулятор скорости САУ ввести одно интегрирующее или изодромное звено. При этом q=1 САУ ЭП становится астатической как по задающему, так и по возмущающему воздействиям [q>l,(1>0)] . Если, при этом (q=1), воздействия ωн.з или Mн.с будут изменяться с постоянной скоростью 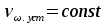 или или 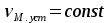 , соответственно(т.е к=1), то в САУ ЭП будет иметь место установившееся отклонение выходной величины Δωн.уст (q=k=1)как от изменения заданного значения этой величины , так и от изменения момента сопротивления нагрузки, т.е. Δωн.уст (ωн.з.) , соответственно(т.е к=1), то в САУ ЭП будет иметь место установившееся отклонение выходной величины Δωн.уст (q=k=1)как от изменения заданного значения этой величины , так и от изменения момента сопротивления нагрузки, т.е. Δωн.уст (ωн.з.) 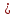 0 или Δωн.уст(Mн.с. ) при 0 или Δωн.уст(Mн.с. ) при 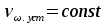 или или 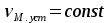 ,соответственно, необходимо в регулятор скорости САУ ввести еще одно (итого два) интегрирующее или изодромное звено. При этом q=2, ,соответственно, необходимо в регулятор скорости САУ ввести еще одно (итого два) интегрирующее или изодромное звено. При этом q=2,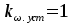 или или 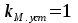 и, следовательно, Δωн.уст(ωн.з.)=0 [q>kω.уст,(2>1)]и Δ ωн.ст(Mн.с.ст )=0 [q>kМ.уст,(2>1)]. и, следовательно, Δωн.уст(ωн.з.)=0 [q>kω.уст,(2>1)]и Δ ωн.ст(Mн.с.ст )=0 [q>kМ.уст,(2>1)].Если же ωн.з или Mн.с будут изменяться с постоянным ускорением (к=2) 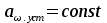 или или 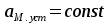 , соответственно, то при двух звеньех интегрирующего типа в РС (q=k=2)в САУ ЭП будет иметь место установившееся отклонение выходной величины Δωн.уст(ωн.з) , соответственно, то при двух звеньех интегрирующего типа в РС (q=k=2)в САУ ЭП будет иметь место установившееся отклонение выходной величины Δωн.уст(ωн.з)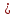 0 или Δωн.уст(Mн.с. ) 0 или Δωн.уст(Mн.с. )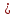 0. для сведения и этих отклонений к нулю необходимо в РС САУ ввести еще одно (итого три) звено интегрирующего типа. При этом q=3,к=2, q>k и по любому внешнему воздействию статическому или установившемуся (по скорости или по ускорению) Δωн.уст по соответствующему воздействию будет равно нулю. 0. для сведения и этих отклонений к нулю необходимо в РС САУ ввести еще одно (итого три) звено интегрирующего типа. При этом q=3,к=2, q>k и по любому внешнему воздействию статическому или установившемуся (по скорости или по ускорению) Δωн.уст по соответствующему воздействию будет равно нулю.Окончательное количество вводимых звеньев интегрирующего типа в РС будет определяться в следующем разделе по мере выполнения требований к качеству управления, точности и устойчивости работы системы САУ ЭП. Список использованной литературы: Сазонов В.В. Анализ и синтез системы автоматического управления электрическим приводом постоянного тока [Текст]: методические указания к выполнению курсового проекта по дисциплине «Теоретические основы автоматики, телемеханики и связи» для студентов спец. «АТС на ж/д транспорте» всех форм обучения/ В.В. Сазонов, Л.А.Плешакова. – Самара: СамГАПС, 2005.-36 с. (в библиотеке СамГУПС №1633). Сазонов В.В. Анализ и синтез системы автоматического управления электрическим приводом постоянного тока [Текст]: уч. Пособие/Вячеслав Викторович Сазонов. – Самара: СамГАПС, 2005.-176 с. Сазонов В.В. Методические указания по использованию пакета динамического моделирования VisSim при выполнении курсового проекта и лабораторных работ по дисциплине «Теоритические основы автоматики, телемеханики и связи» [Текст]: для студентов спец. «АТС на ж/д транспорте» всез форм обучения / В.В.Сазонов. – Самара: СамГАПС, 2005.-68 с. (В библиотеке СамГУПС № 1642). |
