ТОАТ КУРСОВОЙ. Реферат Построение функциональной схемы сау эп
 Скачать 1.23 Mb. Скачать 1.23 Mb.
|
|
Содержание Реферат……………………………………………………………………………2 1 Построение функциональной схемы САУ ЭП…………………………….3-5 2 Построение структурных схем ДПТ и механической части ЭП………..6-10 3 Выбор ДПТ и расчет параметров звеньев структурных схем………..…11-14 4 Построение структурной схемы тиристорного преобразователя………15-21 5 Построение структурной схемы ЭП и её преобразование…………...…22-25 6 Исследование статических и динамических………………………….…26-31 характеристик ЭП на модели 7 Анализ САУ ЭП с пропорциональным законом управления………..…32-34 8 Исследование САУ ЭП с П-регулятором на модели………………...…35-47 9 Построение статических САУ ЭП……………………………………..…48-49 Список использованной литературы………………………………………….50 РЕФЕРАТ Курсовой проект Пояснительная записка: 49 с., 24 рис., 3 источника. Система автоматического управления, электрический привод, функциональная схема, тиристорный преобразователь, двигатель, структурная схема, П – регулятор, Спроектировали систему автоматического управления электрическим приводом постоянного тока (САУ ЭП), обеспечивающую выполнение заданных требований к качеству процессов управления. Построение функциональной схемы САУ ЭП. Объектом управления системы управления, которому требуется разработать в курсовом проекте, является ЭП постоянного тока тиристорным преобразовательным устройством. Функциональная схема системы автоматического управления таким ЭП (САУ ЭП) приведена на рисунке 1.1. 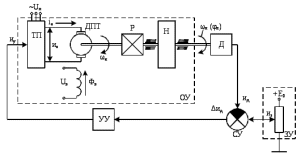 Рисунок 1.1 – Функциональная схема САУ ЭП В ЭП использован двигатель постоянного тока (ДПТ) с независимым возбуждением. Магнитный поток возбуждения Фв создается обмоткой возбуждения, питаемой от независимого источника постоянного напряжения Uв. Цепь якоря ДПТ подключена к выходу управляемого тиристорного преобразователя ТП, преобразующего переменное напряжения сети Uп в постоянное регулируемое напряжение uя. Путем изменения напряжения uя можно изменять угловую скорость вращения якоря ДПТ ωя. Значения uя регулируется сигналом управления uу. Вал якоря ДПТ через редуктор Р связан с механической нагрузкой Н. В зависимости от назначения ЭП регулируемой переменной (у) является угловая скорость вращения (ωн). Целью управления является изменение ωн в соответствии с изменением задающего сигнала (напряжения) uз. Напряжение uз пропорционально заданному значению (ωн.з.) регулируемой переменной: uз= Kз ωн.з., (1.1) где Кз – постоянный коэффициент. Напряжение uз формируется задающим устройством (ЗУ). В простейшем случае таким устройством является потенциометр (рис. 1.5). Напряжение, снимаемое с нижнего плеча потенциометра, пропорционально перемещению его движка. В рассматриваемой системе управления использован принцип обратной связи (по отклонению). Для получения информации о значении регулируемой переменной служит датчик Д. Напряжение uд (uω) на выходе датчика пропорционально значению регулируемой переменной: uω=Кдωн, (1.2) где Кд – постоянный коэффициент. Для получения сигнала, характеризующего отклонение выходной переменной от заданного значения, служит сравнивающее устройство СУ, на выходе которого формируется напряжение Δuω: Δuω=uз-uω (1.3) С учетом (1.1) и (1.2) Δuω=Кз ωн.з-Кдωн, (1.4) Чтобы напряжение Δuω было пропорционально отклонению выходной переменной от заданного значения, следует принять Кд=Кз. Тогда, обозначив эти коэффициенты через Кω получим: Δuω= Кω(ωн.з-ωн)= Кω Δωн, (1.5) где Δωн= ωн.з-ωн. Таким образом, на выходе СУ формируется сигнал, равный не самому отклонению регулируемой переменной от заданного значения, а сигнала, пропорциональный этому отклонению. Однако для процесса управления это не имеет значения, так как правильно спроектированная САУ стремиться уменьшить отклонение Δuω, а следовательно и отклонение Δωн. Напряжение Δωн подается на вход УУ, которое формирует управляющий сигнал (напряжение) uу на основании какого-либо закона управления uу=ƒ(Δuω). Рассмотрим работу ЭП по схеме на рис. 1.1 при использовании наиболее простого закона управления – пропорционального. В этом случае УУ обычно представляет собой усилитель постоянного тока, у которого uу= Kу uω (1.6) где Ку – коэффициент усиления усилителя. Регулируемой переменной является угловая скорость вращения вала нагрузки ωн. В исходном состоянии система выключена, якорь ДПТ не вращается (uя=0, ωя=0, ωн=0), а на выходе задающего устройства установлено некоторое напряжение uз>0.Тогда после пуска системы на выходе СУ, согласно выражению (1.3), появится сигнал Δuω= uз (поскольку непосредственно после пуска имеем ωн=0 и uω=0). На выходе усилителя появится управляющее напряжение uу= Kу uз, вызывающее появление на выходе ТП напряжения uя>0. Под действием этого напряжения якорь ДПТ начнет вращаться, приводя во вращение и нагрузку Н (через редуктор Р). Значение переменной ωн будет постепенно увеличиваться, вызывая увеличение напряжения uω и уменьшение значения сигнала Δuω=uз-uω. В системе будет наблюдаться переходный процесс, который может иметь колебательный или апериодический характер (в зависимости от параметров системы). Если система устойчива, то этот процесс завершится при некотором достаточно малом значении Δuω, когда uω≈uз и ωн≈ωн.з. Полностью устранить отклонение ωн от ωн.з система с регулятором, реализующим пропорциональный закон управления и называемым П-регулятором, не может, так как при ωн=ωн.з на выходе СУ имеем Δuω=0, при этом uу=0, uя=0, якорь ДПТ не вращается. Для формирования сигнала управления uу, соответствующего требуемому значению ωн, обязательно требуется определенное значение сигнала Δuω= Кωωн. Уменьшить значения Δuω и Δωн можно увеличением коэффициента усилителя Ку, однако при этом качество переходных процессов может существенно ухудшиться (возрастет колебательность), а при достаточно больших значениях Ку система может стать не устойчивой. Если задающий сигнал ωн.з изменяется в процессе работы ЭП, то система управления с определенной точностью будет стремиться поддержать значение ωн на уровне ωн.з. Например, при увеличении ωн.з (т.е. uз) возрастают Δuω, uу, uя, ωя и ωн (до значения ωн≈ωн.з). Если uз=const, то система обеспечивает стабилизацию регулируемой переменной (например, ωн). Если в результате каких-либо возмущений произойдет изменение переменной ωн к прежнему или близкому к нему значению. Возмущениями в рассматриваемой системе являются изменения нагрузки на валу редуктора (а следовательно, и ДПТ) и напряжения питания ТП Uп. Если, например, нагрузка на вал возрастет, то якорь ДПТ будет вращаться медленнее, значение ωн уменьшиться. При этом значение напряжения uω уменьшится, а значение напряжения Δuω увеличится, что приведет к увеличению сигнала управления uу, напряжения uя, угловой скорости ωя и переменной ωн.Переходный процесс также закончится при ωн≈ωн.з, однако фактическое значение ωн будет уже иным, так как для приведения в действии возросшей нагрузки требуется больше значение напряжения uя, а следовательно, напряжений uу и Δuω. Большему значению Δuωсоответствует и большее значение отклонения Δωн. 2. Построение структурных схем ДПТ и механической части ЭП. Принцип работы ДПТ основан на взаимодействии магнитного поля и находящего в нем проводника с током. Магнитное поле в ДПТ обычно создается обмоткой возбуждения, расположенной на полюсах статора. Проводник выполняют в виде обмотки, расположенной в пазах якоря. За счет сил Fn, действующих на витки этой обмотки, создается электромагнитный (вращающий) момент якоря Мэм зависящий от числа витков обмотки, диаметра якоря и других параметров. Обычно выражение для момента Мэм записывают в виде: Мэм=СмФвiя, (2.1) где См - постоянный коэффициент, зависящий от конструктивных параметров ДПТ; Фв - магнитный поток возбуждения, создаваемый обмоткой возбуждения; iя- ток в цепи якоря. Поскольку обмотка возбуждения питается от независимого источника, и ток возбуждения постоянен, то магнитный поток Фв также постоянен. Поэтому можно записать Мэм=Кмiя, (2.2) где Км=СмФв – постоянная величина. Если входной величиной ДПТ считать ток якоря iя, а выходной - электромагнитный момент Мэм, создаваемый обмоткой якоря, то ДПТ является безынерционным звеном, поскольку вращающий момент Мэм создается силами, действующими на витки обмотки якоря, а эти силы в любой момент времени при Фв = const зависят только от тока, протекающего по виткам в тот же момент времени. Если же входной величиной ДПТ считать ток iя, а за его выходную величину принять угловую скорость вращения якоря ωя, то ДПТ уже не является безынерционным звеном, поскольку значение ωя в любой момент времени не определяется значением тока iя в тот же момент времени. Если предположить, что ток iя резко (скачком) увеличится, то также скачком (без задержки) возрастет и момент Мэм. Однако ωя скачком возрасти не может из-за инерционности вращающихся механических частей ДПТ (якоря, коллектора и т. д.). Кроме того, входной величиной ДПТ по цепи якоря чаще является не ток iя, а напряжение на якоре uя. Установим связь тока iя с напряжением на якоре uя. При этом следует учесть и влияние на ток iя ЭДС еЯ индуцированной в обмотке якоря при ее вращении в магнитном поле. В динамике эта связь может быть выражена вторым законом Кирхгофа, согласно которому 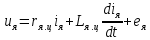 (2.3) (2.3)где rя.ц- полное активное сопротивление якорной цепи [в общем случае оно включает в себя сопротивления обмоток якоря, щеточных контактов, щеток, сопротивления обмоток дополнительных полюсов и последовательной (компенсационной) обмотки]; Lя.ц- полная индуктивность якорной цепи. Вторая составляющая напряжения uя в выражении (2.3) представляет собой ЭДС самоиндукции, которая возникает в якорной цепи только при изменении тока iя, например, во время переходных процессов; от ωя эта ЭДС не зависит. В то же время ЭДС еЯ зависит от ωя и не зависит от тока iя. За счет индуктивности Lя.ц ток iя, а стало быть и момент Мэм, не могут возрасти скачком при скачке напряжения uя. Следовательно, индуктивность обуславливает дополнительную инерционность ДПТ (помимо инерционности его вращающихся частей) по отношению к управляющему воздействию. Структурную схему звена, связывающего якоря ДПТ ток iя с переменными величинами uя и еЯ, легко получить на основании дифференциального уравнения (1.9), записав его в символической форме: 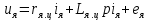 (2.4) (2.4)или 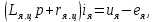 ооткуда 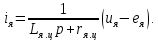 (2.5) (2.5)В соотношении (1.11) выражение 1/(Lя.цp+rя.ц) представляет собой передаточную функцию, связывающую ток iя с напряжением uя и ЭДС ея (в данном случае - с их разностью). После преобразования этой функции стандартному виду получаем: 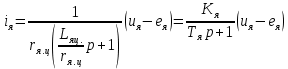 , (2.6) , (2.6)где Кя=1/rя.ц - постоянный коэффициент, представляющий собой проводимость якорной цепи; Тя= Lя.ц/rя.ц - постоянная времени цепи якоря ДПТ. Зависимость электромагнитного момента Мэм от тока якоря iя определяется соотношением (2.2), в котором коэффициент Кмявляется передаточной функцией, характеризующей связь Мэми iя. На основании соотношений (2.2) и (2.6) легко построить структурную схему звена, отображающего связь момента Мшс переменными величинами ияи ея; эта схема показана на рис. 1.10.  Рисунок 1.10 В построенной схеме напряжение ия формируется тиристорным преобразователем и является по отношению к ДПТ внешним управляющим воздействием. В то же время ЭДС ея является результатом функционирования самого ДПТ. Эта ЭДС образуется при пересечении магнитного поля витками обмотки якоря (согласно закону электромагнитной индукции) и зависит от скорости этого пересечения, т. е. от скорости вращения якоря. Значение ЭДС, индуцированной во всей обмотке якоря, можно определить по формуле: ея=СяФвωя, где Ся - конструктивная постоянная двигателя. Добавив в структурную схему на рис. 1.10 звено с передаточной функцией (коэффициентом) СЯФВ, связывающей переменные еяи ωя, получим более полную структурную схему ДПТ, приведенную на рис. 1.11. 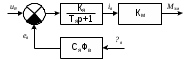 Следует отметить, что момент Мэм, развиваемый якорем, еще не является моментом на валу ДПТ. В двигателе имеются потери мощности, обусловленные трением в подшипниках, трением между щетками и коллектором, вентиляционными потерями, возникающими при вращении якоря и вентилятора, расположенного на его валу. Поэтому часть момента Мэмтребуется затратить на преодоление трения и вентиляционные потери. Если обозначить эту часть момента Мэмчерез Мд.пот., то момент на валу ДПТ (Мд) равен: Мд=Мэм-Мд.пот. (2.7) Момент Мд.потявляется реактивным (§ 1.1) и всегда действует в направлении, противоположном направлению вращения якоря ЭД. Кроме того, в реальных ЭД Мд.пот зависит от ωя (особенно та его часть, которая обусловлена вентиляционными потерями). Тем не менее при упрощенных расчетах обычно принимают 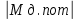 = const Тогда характеристика Мд.пот(ωя) имеет вид и описывается выражением: = const Тогда характеристика Мд.пот(ωя) имеет вид и описывается выражением:Мд.пот= 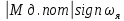 (2.8) (2.8)С учетом момента Мд.пот структурная схема ДПТ принимаем вид, показанный на рисунке 1.12. Выходной переменной в этой схеме является момент на валу двигателя Мд. 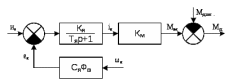 Рисунок 1.12 В схеме на рис. 1.12 выходной переменной является момент Мд на валу ДПТ, а входными воздействиями, определяющими значение Мд, являются напряжение ияи угловая скорость ωЯ (при Мд.пот= const). В то же время в большинстве ЭП регулируемой переменной является угловая скорость вращения якоря ωя. Вращение якоря обусловлено действием электромагнитного момента Мэм, при этом значение ωя зависит от момента сопротивления, создаваемого нагрузкой, а в переходных режимах - и от инерционности движущихся механических элементов ЭП. Полная структурная схема ЭП не может быть построена без анализа процессов, происходящих в его механической части. Обычно в эту часть включают движущиеся части ЭД, передаточное устройство (редуктор) и исполнительный орган (нагрузку). В общем случае механическая часть ЭП представляет собой сложную систему элементов конечной жесткости с различными массами (сосредоточенными и распределенными) и с различными скоростями движения; на эти массы воздействуют различные силы и моменты. Принимаем допущение, что все вращающиеся элементы механической части ЭП жестко связаны между собой, т.е. не имеют упругих деформаций (все элементы являются обсалютно жесткими), и по отношению к процессу движения могут рассматриваться кА один элемент. Механические системы такого типа принято называть одномассовыми. Движение одномассовой механической системой (второй закон динамики для вращательного движения) описывается уравнением: 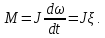 (2.9) (2.9)Это уравнение аналогично уравнению динамики (второму закону Ньютона) для прямолинейного движения тела 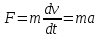 (2.10) (2.10)В этих уравнениях движения M – полный суммарный момент внешних сил, равный алгебраической сумме моментов всех внешних сил, действующих на тело, относительно оси вращения; Ω – угловая скорость вращения тела; 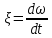 – его угловое ускорение; J – общий (суммарный) момент инерции вращающихся частей рассматриваемой механической системы. – его угловое ускорение; J – общий (суммарный) момент инерции вращающихся частей рассматриваемой механической системы.Момент инерции J по отношению к вращательному движению тела играет ту же роль, что и масса (m) по отношению к его поступательному движению. J относительно оси – величина являющаяся мерой инерции тела во вращательном движении вокруг этой оси, m – масса тела служит мерой инерции в поступательном движении. Если ЭП включает в себя ещё и передаточное устройство (редуктор), связывающее нагрузку с ЭД, то механическая часть ЭП представляет собой более сложную систему связанных между собой механических элементов. Эти элементы могут иметь различные скорости вращения и различные моменты инерции. Для жесткого редуктора коэффициент редукции r равен 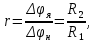 (2.11) (2.11)Откуда, 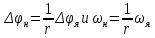 (2.12) (2.12)Для упрощения расчетов реальную механическую систему обычно представляют в виде модели, в которой все элементы, движущиеся с различными скоростями, приводят к какой-нибудь одной скорости. Применительно к ЭП в качестве такой скорости используют угловую скорость вращения вала якоря ДПТ-ωя. За счет передаточного устройства изменяются условия передачи вращающего момента от ЭД к нагрузке и момента сопротивления, оказываемого нагрузкой на ЭД. Если рассматривать передачу вращающего момента от ЭД к нагрузке, то момент Мдн, оказываемый двигателем на нагрузку через редуктор, увеличивается в r раз. Это и является главным достоинством редуктора, поскольку он делает возможным приведение в действие больших нагрузок с помощью ЭД небольшой мощности. Мдн=rMд. (2.13) При этом предполагается, что редуктор не имеет потерь, т.е. если рассматривать действие нагрузки на вал ЭД через редуктор, то момент Мн на выходном валу редуктора передается на вал ЭД в r раз ослабленным. Двигатель воспринимает момент сопротивления нагрузки вr раз уменьшенным, что и делает возможным нормальную работу ЭД при больших моментах нагрузки. В переходных режимах работы ЭП редуктор уменьшает и влияние той части момента сопротивления нагрузки, т.е. момент инерции нагрузки по отношению к вращению вала ЭД также изменяется. Уравнение динамики вращения нагрузки имеет вид: 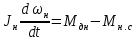 (2.14) (2.14) |
