Случайные события. случайные события. Реферат Теория вероятности. Случайные события. Теория вероятности. Случайные события
 Скачать 158.49 Kb. Скачать 158.49 Kb.
|
    minaychenko_ekaterina@mail.ru Минайченко Екатерина 1 группа Институт психологии. Факультет психологии человека и социального взаимодействия. реферат Теория вероятности. Случайные события. Теория вероятности. Случайные события. Основное положение теории. Теория вероятности - это наука, занимающаяся изучением закономерностей массовых случайных явлений. Такие же закономерности, только в более узкой предметной области социально-экономических явлений, изучает статистика. Между этими науками имеется общность методологии и высокая степень взаимосвязи. Практически любые выводы сделанные статистикой рассматриваются как вероятностные. Особенно наглядно вероятностный характер статистических исследований проявляется в выборочном методе, поскольку любой вывод сделанный по результатам выборки оценивается с заданной вероятностью. Случайные события, их классификация. Понятие «случайное событие»: пусть проводится некоторый опыт (эксперимент, наблюдение, испытание), исход которого предсказать заранее нельзя. Такие эксперименты в теории вероятностей называют случайными. При этом рассматриваются только такие эксперименты, которые можно повторять, хотя бы теоретически, при неизменном комплексе условий произвольное число раз. Случайным событием называется любой исход опыта, который может произойти или не произойти.        СЛУЧАЙНЫЕ НЕВОЗМОЖНЫЕ ДОСТОВЕРНЫЕ СОБЫТИЯ Достоверным является событие, которое в результате испытания обязательно произойдет. Например, камень упадет вниз. Невозможным является событие, которое заведомо не произойдет в результате испытания. Например, камень при падении улетит вверх. Случайным называется событие, которое в результате испытания может произойти, а может не произойти. Например, из колоды карт вытащили туза. События обозначаются, как правило, заглавными буквами латинского алфавита: А, В, С, ... Пример 1. Опыт: бросание игральной кости; событие А - выпадение 5 очков, событие В - выпадение четного числа очков, событие С - выпадение 7 очков, событие D - выпадение целого числа очков, событие Е - выпадение не менее 3-х очков, …. Непосредственные исходы опыта называются элементарными событиями. Обозначение: w, wi. Совокупность всех элементарных событий, соответствующих опыту, называется пространством элементарных событий. Обозначение: W = {w}. Любое подмножество множества W называется событием. События и действия над ними можно наглядно иллюстрировать с помощью диаграмм Эйлера-Венна: 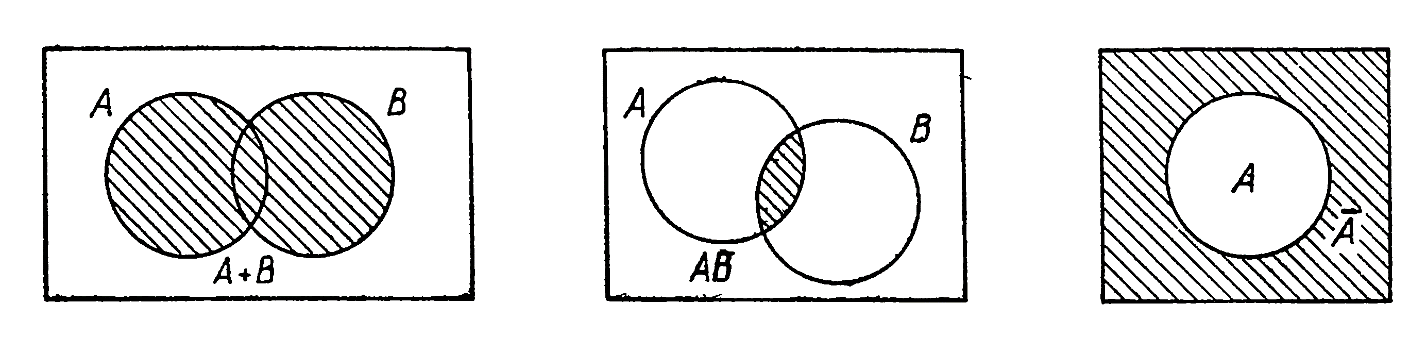 Вероятность случайных событий. Любое случайное событие обладает какой-то степенью возможности, которую в принципе можно измерить численно. Чтобы сравнивать события по степени их возможности, нужно связать с каждым из них какое-то число, которое тем больше, чем больше возможность события. Это число мы и назовем вероятностью события. Какое бы событие A мы бы ни взяли, его вероятность P(A) удовлетворяет условию: 0 Событие A называется практически невозможным, если его вероятность не в точности равна нулю, но очень близка к нулю: P(A) 0 практически достоверным является событие, вероятность которого не в точности равна единице, но очень близка к единице: P(A) 1 Противоположным событию А называется событие А, состоящее в непоявлении события А. Пример. Опыт: Один выстрел по мишени. Событие А - попадание в десятку. Противоположное событие А - непопадание в десятку. Если какое-то событие А практически невозможно, то противоположное ему событие А практически достоверно и наоборот. Практически невозможные (и сопутствующие им практически достоверные) события играют большую роль в теории вероятностей: на них основана вся её познавательная ценность. Ни один прогноз в области случайных явлений не является и не может являться полностью достоверным; он может быть только практически достоверным, т. е. осуществляться с очень большой вероятностью. Существует класс опытов, для которых вероятности их возможных исходов можно вычислить, исходя непосредственно из самих условий опыта. Для этого нужно, чтобы различные исходы опыта обладали симметрией и в силу этого были объективно одинаково возможными. Принцип практической уверенности. В основе применения всех выводов и рекомендаций, добываемых с помощью теории вероятностей, лежит принцип практической уверенности, который можно сформулировать следующим образом: Если вероятность события А в данном опыте весьма мала, то (при однократном выполнении опыта) можно вести себя так, как будто событие А вообще невозможно, т. е. не рассчитывать на его появление. Если кубик выполнен симметрично, "правильно" (центр тяжести не смещен ни к одной из граней), естественно предположить, что любая из граней будет выпадать так же часто, как каждая из остальных. Так как достоверное событие "выпадает какая-то из граней" имеет вероятность, равную единице, и распадается на шесть одинаково равных вариантов (1, 2, 3, 4, 5 или 6 очков), то естественно приписать каждому из них вероятность, равную 1/6. Для всякого опыта, обладающего симметрией возможных исходов, можно применить аналогичный прием, который называется непосредственным подсчетом вероятностей. Равновозможные события. Если опыт обладает симметрией возможных исходов, то случаи представляют собой набор его равновозможных и исключающих друг друга исходов. Про такой случай говорят, что он сводится к схеме случаев. Для таких опытов возможен непосредственный подсчет вероятностей, основанный на подсчете доли так называемых благоприятных случаев в общем их числе. Случай называется благоприятным (или "благоприятствующим") событию A, если появление этого случая влечет за собой появление данного события. Если опыт сводится к схеме случаев, то вероятность события A в данном опыте можно вычислить как долю благоприятных случаев в общем их числе: P(A)=m/n, где m - число случаев, благоприятных событию A; n – общее число случаев. Данная формула, так называемая "классическая формула" для вычисления вероятностей, предложенная еще в XVII веке, когда главным полем приложения теории вероятностей были азартные игры ( в которых симметрия возможных исходов обеспечивается специальными мерами), долгое время ( вплоть до XIX века ) фигурировала в литературе как " определение вероятности "; те задачи, в которых схема случаев отсутствует, искусственными приемами сводились к ней. В настоящее время формального определения вероятности не дается, т. к. это понятие считается первичным и не определяется. В данное время для вычисления вероятностей применяется закон распределения Пуассона. Распределением Пуассона описываются : а) показания счетчика, снимаемые через каждый интервал времени Т; б) число зарегистрированных событий. Распределение Пуассона играет большую роль в практическом применении теории вероятностей: многие физические явления приводят именно к такому распределению вероятностей. |
