ФОРМУЛА ЛОГИКИ ПРЕДИКАТОВ И ЕЕ ЗНАЧЕНИЕ.. Реферата Теория. Основные понятия, связанные с предикатами Равносильные формулы логики предикатов
 Скачать 1.38 Mb. Скачать 1.38 Mb.
|
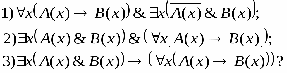 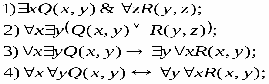 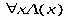 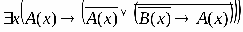 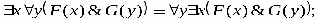 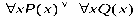 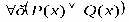 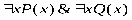 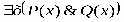 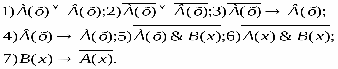 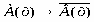 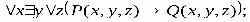 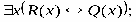 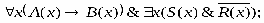 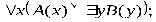 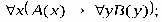 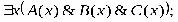 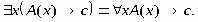 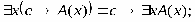 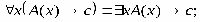 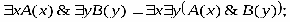 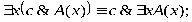 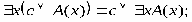 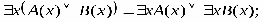 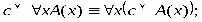 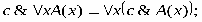 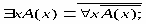 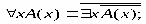 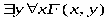 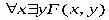 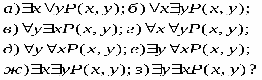 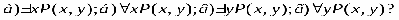 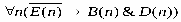 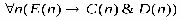 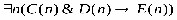 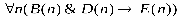 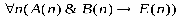 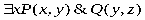 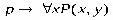 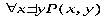 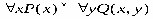 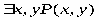 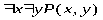 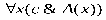 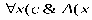 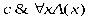 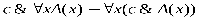 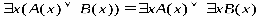 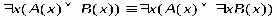 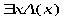 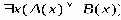 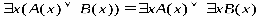 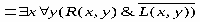 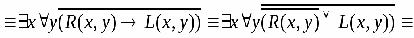 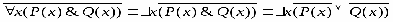 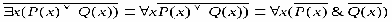 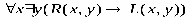 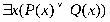 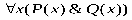 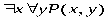 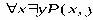 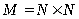 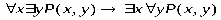 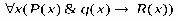 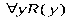 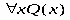 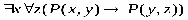 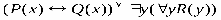 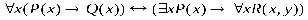 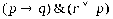 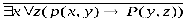 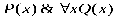 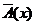 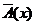 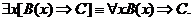 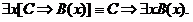 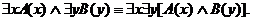 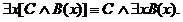 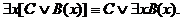 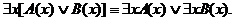 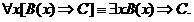 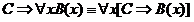 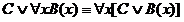 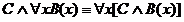 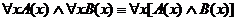 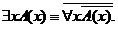 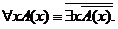 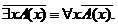 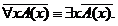 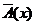 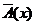 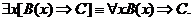 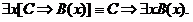 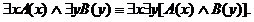 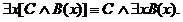 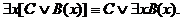 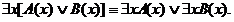 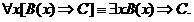 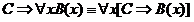 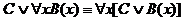 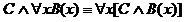 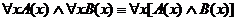 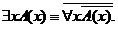 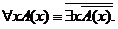 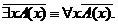 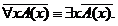 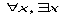 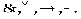 ПЛАН РЕФЕРАТА: ПЛАН РЕФЕРАТА:
ТЕОРИЯ. ОСНОВНЫЕ ПОНЯТИЯ, СВЯЗАННЫЕ С ПРЕДИКАТАМИ В логике предикатов используется следующая символика:
1. Каждое высказывание как переменное, так и постоянное, является формулой.
РАВНОСИЛЬНЫЕ ФОРМУЛЫ ЛОГИКИ ПРЕДИКАТОВ.Определение1.Две формулы логики предикатов А и В называются равно сильнымина о бластиМ,если они принимают одинаковые логические значения при всех значениях входящ в них переменных, отнесенных к области М. Определение2.Две формулы логики предикатов А и В называются равно сильными, если он равносильны на всякой области. Ясно, что все равносильности алгебры высказываний будут верны, если в них вместо переменных высказываний подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов. Рассмотрим основные из этих равносильностей. Пусть А(х) и В(х) – переменные предикаты, а С – переменное высказывание (или формула, н содержащая х). Тогда имеют место равносильности: 1. 2. 3. 4 5. 6. . 7. 8. 9. 10. 11. 12. 13. 14. 15. Равносильность 1 означает тот простой факт, что, если не для всех х истинно А(х), то существует х, при котором будет истиной . Равносильность 2 означает тот простой факт, что, если не существует х, при котором истинно А(х), то для всех х будет истиной . Равносильности 3 и 4 получаются из равносильностей 1 и 2, соответственно, если от обеих и частей взять отрицания и воспользоваться законом двойного отрицания. ЗАКОНЫ ЛОГИЧЕСКИХ ОПЕРАЦИЙ.(общезначимые формулы логики предикатов) Равносильныеформулылогикипредикатов. Определение1.Две формулы логики предикатов А и В называются равно сильнымина о бластиМ,если они принимают одинаковые логические значения при всех значениях входящ в них переменных, отнесенных к области М. Определение2.Две формулы логики предикатов А и В называются равно сильными, если он равносильны на всякой области. Ясно, что все равносильности алгебры высказываний будут верны, если в них вместо переменных высказываний подставить формулы логики предикатов. Но, кроме того, имеют место равносильности самой логики предикатов. Рассмотрим основные из этих равносильностей. Пусть А(х) и В(х) – переменные предикаты, а С – переменное высказывание (или формула, н содержащая х). Тогда имеют место равносильности: 1. 2. 3. 4. 5. 6. . 7. 8. 9. 10. 11. 12. 13. 14. 15. Равносильность 1 означает тот простой факт, что, если не для всех х истинно А(х), то существует х, при котором будет истиной . Равносильность 2 означает тот простой факт, что, если не существует х, при котором истинно А(х), то для всех х будет истиной . ПРИМЕРЫ ЗАДАЧС ИСПОЛЬЗОВАНИЕМ ФОРМУЛ ЛОГИКИ ПРЕДИКАТОВ Пример 1. Какие из следующих выражений являются формулами логики предикатов? каждой формуле выделите свободные и связанные переменные.
4); 5); 6). Решение. Выражения 1), 2), 4), 6) являются формулами, так как записаны в соответствии определением формулы логики предикатов. Выражения 3) и 5) не являются формулами. выражении 3) операция конъюнкция применена к формулам Р(х) и; в первой из н переменнаях свободна, а во второй связана квантором общности, что противореч определению формулы. В выражении 5) квантор существования по переменной унавешен формулу , в которой переменнаяусвязана квантором общности, что также против речит определению формулы. В формуле 1) переменная у свободна, а переменные х и zсвязаны. В формуле 2) н предметных переменных. В формуле 4) переменная хсвязана, а переменная усвободна. О логическом значении формулы логики предикатов можно говорить лишь тогда, когда зада множество М,на котором определены входящие в эту формулу предикаты. Логическ значение формулы логики предикатов зависит от значения трех видов переменных, входящ в формулу: а) переменных высказываний; б) свободных предметных переменных из множества М; в) предикатных переменных. При конкретных значениях этих переменных формула принимает конкретное логическ значение. Пример 2. Дана формула ,где предикаты Р(х),Q(х) и R(х) определен на множестве N. Найти ее значение, если
12. Но тогда при всех х,если число хделится на 12, то оно делится и на 2, и, значит, в случае формула истинна. Так как из делимости числа хна 12 не при всех хследует делимость числа хна 5, то в случ
Пример 3. Вычислить значение формулы ,если предикат Р(х,у)имеет значение Р°(х,у) —«число хмень числа у»и определен на множестве . Решение. Так как при указанном значении предиката Р(х,у)высказывание означает утверждение, что для любого натурального числа х найдется натуральн число у,большее числа х,то это высказывание истинно. В то же время высказывани означает утверждение, что существует натуральное число х,которое мень любого натурального числа у.которое ложно. При этом исходная формула, очевидно, ложна. Определение 2. Две формулы логики предикатов А и Вназываютсяравносильными областиМ,если они принимают одинаковые значения при всех значениях входящих в н переменных, отнесенных к области М. Две формулы логики предикатов Аи Вназываютсяравносильными,если они равносильны всякой области. Здесь, как и в алгебре высказываний, для равносильных формул принято обозначение А≡В Ясно, что все равносильности алгебры высказываний будут верны, если в них вмес переменных высказываний подставить формулы логики предикатов. Но, кроме того, име место равносильности самой логики предикатов. Сюда, в первую очередь, следует отнес равносильности: , . Они широко используются в логике предикатов при равносильных преобразованиях, ес приходится иметь дело с выражениями, содержащими операцию отрицания. Пример 4. Найти отрицание следующих формул: 1) ; 2) ; 3). Решение. 1); 2)
Доказательство равносильностей логики предикатов требует или детального рассмотрен значений формул или использования известных равносильностей. Пример 5. Доказать равносильность . Решение. Для доказательства равносильности достаточно рассмотреть два случая:
.
Следовательно,. Пример 6. Доказать равносильность . Решение. Рассмотрим два случая:
. Значит, в этом случае обе исходные формулы тождественно ложны.
будут ложными, то есть ложные значения принимают обе исходные формул что в итоге доказывает их равносильность.
«число пделится па 4», D(n)«число n делится на 6», Е(п): «число n делится на 12». Укажит какие из следующих утверждений истинны, какие ложны: 1) ; 2); 3); 4); 5);
1. «Треугольник ABCпрямоугольный» и «Треугольник ABCтупоугольный»;
5) «Натуральное число n- простое» и «Натуральное число n - составное.»
2) 3) 4) 5) 6) 7) 8) 9) 10) 11)
2) 3) 4) 5) 6)
3) можно ли в 1) и 2) заменить F(x) и G(y)двухместными предикатами, зависящими от x и y?
Решение задачи по математической логике Исчисление предикатов Дано универсальное множество = {e,d,f,c,g,a,h,b,o,u,l} и два подмножества J={f, b, g, h, a, c} и I={o, h, b, l, u, a}; два предиката C(x)=" x принадлежит J" и В(x)=" x принадлежит I". Найдите область истинности предикатов: P1(x)=C(x)∨B(x); P2(x)=C(x)→B(x); P3(x)=C(x)B(x); P4(x)=C(x)&B(x) Решение. Универсальное множество U = {e, d, f, c, g, a, h, b, o, u, l}. Область истинности предиката С(x): J={f, b, g, h, a, c}. Область истинности предиката B(x): I={o, h, b, l, u, a}. Область истинности предиката P1(x)=C(x)∨B(x): J⋃ I={f, b, g, h, a, c, o, l, u}. Область истинности предиката P2(x) = C(x)→B(x):J I(U\ J) I ={e, d, o, u, l}⋃{o, h, b, l, u, a}={e, d, o, u, l, h, b, a}. Т.к. C( x) ∼ B( x) (C(x) B( x)) & (C( x) B(x)) , то область истинности предиката P3(x)=C(x)B(x) – это элементы, принадлежащие области пересечения множеств J∩ I(оба предиката при этих элементах истинны), и элементы, не принадлежащие ни одному из этих множеств (оба предиката при этих элементах ложны): {e, d, a, h, b}. Область истинности предиката P4(x)=C(x)&B(x): J∩ I= {b, h, a}.
«Через две различные точки проходит единственная прямая» Решение. Введем элементарные предикаты наименьшей местности Pxxточка, Lxxпрямая, Bx, yх проходит через у, Nx, yх не совпадает с у. Тогда формулу «Через две различные точки проходит единственная прямая»можно записать в следующем виде: xyPxPyNx, y⇒ ⇒ zLzBz, xBz, ywLwBw, xBw, y⇒ Nz, w То есть для любых двух не совпадающих точекx, yсуществует прямая z, которая проходит через данные точки и любая прямая w, также проходящая через эти точки, совпадает с z (то есть z единственная такая прямая).Приведем формулу к предваренной нормальной форме. Исключаем импликации: xyPxPyN x, y
Заносим отрицания до атомарных формул.xyPxPyNx, y
Задача скачана с сайта www.MatBuro.ru Еще примеры: https://www.matburo.ru/ex_subject.php?p=dm ©МатБюро - Решение задач по математике, экономике, статистике xyPxPyNx, y
Переименовываем связанные переменные. Нет необходимости.xyPxPyNx, y
Переносим кванторы в начало формулы.xyzwPxPyNx, y
Получили предваренную нормальную форму.Задача 3. Составить предваренную нормальную форму: xyPx, yyPy, xyQx, yQy, x& zPz Решение.Применяем алгоритм приведения к ПНФ, используя законы логики предикатов: Px, yPy, x Переименовываем переменную:yPy, xy2 Py2 , x Преобразуем:xy1Px, y1 y2 Py2 , xy1 Qx, y1 Qy1 , x& zPz Далее преобразуем импликации: PQPQ Преобразуем:xy1Px, y1 y2 Py2 , xy1 Qx, y1 Qy1 , x& zPz убираем двойное отрицаниеxy1Px, y1 y2 Py2 , xy1 Qx, y1 Qy1 , x& zPz Qx, y1 Qy1, x xy1Px, y1 y2 Py2 , xy1 Qx, y1 & zPz Продвигаем отрицания вглубьxy1Px, y1 y2 Py2 , xy1 Qx, y1 & zPz xy1Px, y1 y2Py2 , xy1 Qx, y1 & zPz xy1Px, y1 y2Py2 , xy1 Qx, y1 & zPz xy1Px, y1 y2Py2 , xy1 Qx, y1 & zPz Выносим кванторы.xy1Px, y1 y2Py2 , xy1 Qx, y1 & zPz xy1y2 Px, y1 Py2 , xy1zQx, y1 & Pz xy1y2zPx, y1 Py2 , xQx, y1 & Pz
Какие вхождения переменных являются свободными,а какие связанными в следующей формуле: ∀ ( , ) → ∀ ( ). Решение Переменные, не связанные квантором, называют свободными переменными. В сложной предикатной формуле любая переменная может быть свободной, связанной, а также связанной и свободной. В данной формуле есть две переменные и . Переменная входит два раза (в выражения ∀ и ( , )); переменная входит три раза (в выражения ( , ), ∀ и ( )). Анализируя действия кванторов и количество вхождений переменных, можно определить, что:
связанными, так как квантор ∀ действует на выражение ( , ).
| |||||||||||||||||||||||||||||||||||||||||||
