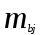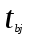РГР Эконометрика регрессия и корреляция. Эконометрика ргр. Регрессия и корреляция
 Скачать 146.77 Kb. Скачать 146.77 Kb.
|
|
Парная регрессия и корреляция 1. Построим уравнения парной линейной регрессии вида 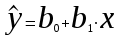 для переменных y, x1. для переменных y, x1.Параметры b0 и b1 уравнения линейной регрессии рассчитываются методом наименьших квадратов путем решения системы нормальных уравнений: 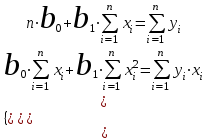 Для нахождения параметров b0 и b1 используем ППП «Анализ данных» MS Excel. Результаты расчетов приведены в приложении 1. Уравнения регрессии имеют вид: Для пары признаков y, x1 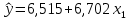 (1) (1)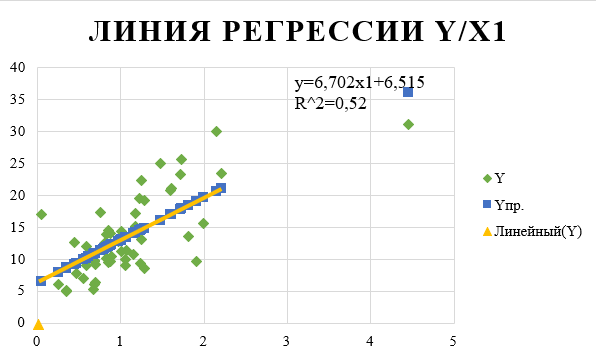 Рис. 1. Линия регрессии 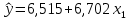 на корреляционном поле. на корреляционном поле.2. Оценим полученное уравнение регрессии через среднюю ошибку аппроксимации и F-критерий Фишера, t-критерий Стьюдента. Найдем среднюю относительную ошибку аппроксимации по формуле:  . .Для вычисления 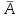 составим расчетные таблицы (см. приложение 2). составим расчетные таблицы (см. приложение 2).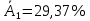 Т.к. значения средней относительной ошибки аппроксимации для уравнения парной линейной регрессии > 12%, уравнениe не даёт хорошую точность. Исследование статистической значимости уравнения регрессии в целом проводится с помощью F-критерия Фишера. Выдвинем гипотезу Н0 о том, что уравнение в целом статистически незначимо, при конкурирующей гипотезе Н1: уравнение в целом статистически значимо. Расчетное значение критерия находится по формуле: 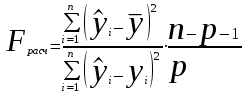 . .Для парного уравнения p=1. Табличное (теоретическое) значение критерия находится по таблице критических значений распределения Фишера-Снедекора по уровню значимости по уровню значимости α и двум числам степеней свободы k1 = p = 1 и k2 = n - p - 1 = 51. 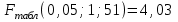 Если Fрасч Для уравнения (1) Fрасч = 54,737, неравенство (2) невыполняется. Проверим статистическую значимость оценок параметров уравнения b0, b1 с помощью t‑критерия Стъюдента. Выдвигается гипотеза Н0: параметр bj = 0 (j = 0, 1) (статистически незначим, случайно отличается от 0), при конкурирующей гипотезе Н1: параметр bj ≠ 0 (статистически значим, неслучайно отличается от 0). Находится расчетное значение критерия 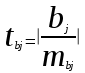 , ,где среднеквадратические ошибки параметров bj равны 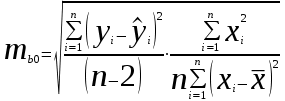 , ,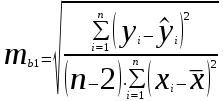 . .Теоретическое значение критерия tтабл находится по таблице критических значений распределения Стъюдента по уровню значимости α и числу степеней свободы k = n - p - 1 . Если tbj > tтабл , то гипотеза Н0 отвергается с вероятностью ошибки α , т.е. оценка коэффициента регрессии bj признается статистически значимой, в противном случае (tbj < tтабл) - незначимой. Табличное значение критерия для уровня значимости α=0,05 и числа степеней свободы k = n - 2 = 51 равно 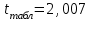 Найдем доверительные интервалы для параметров b0 и b1 уравнения (1). ∆b0= tтабл·mb0=2,007·1,1=2,30; ∆b1 = tтабл·mb1 =2,007·0,9=1,82. Сами доверительные интервалы имеют вид: 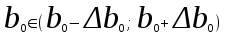 ; ;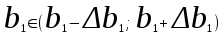 . .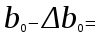 6,515-2,30=4,22 6,515-2,30=4,22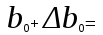 6,515+2,30=8,81 6,515+2,30=8,81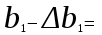 6,702-1,82=4,88 6,702-1,82=4,88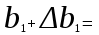 6,702+1,82=8,52 6,702+1,82=8,52Результаты расчетов (см. приложение 1) приведены в таблицe 1. Таблица 1. Проверка критерия Стъюдента
Доверительный интервал для параметра b0 имеет одинаковые знаки, что подтверждает вывод критерия Стъюдента о его статистической значимости. 3. Коэффициент корреляции находится по формуле: 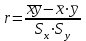 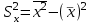 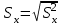 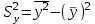 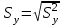 Коэффициент корреляции для пары признаков y и x1 r=0,719 (см. приложение 1) . Следовательно, между показателями y и x1 практически нет линейной связи. Коэффициент детерминации для пары признаков y и x1: R2=r2=(0,719)2=0,52 Т.е. всего 52% изменчивости y объясняется показателем x1. 4. Найдем прогнозное значение yпр путем подстановки значения x1пр в уравнение регрессии 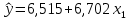 xпр = 1,07*1,05 = 1,125 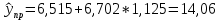 Стандартную ошибку прогноза найдем по формуле 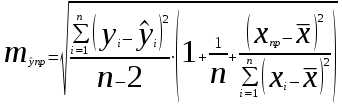 = 4,45 = 4,45Результаты расчетов приведены в приложении 2. 5. Определим с помощью коэффициентов эластичности силу влияния признаков xj на результирующий признак y. Для парного линейного уравнения регрессии средний коэффициент эластичности находится по формуле: 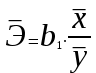 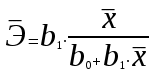 Для признаков y и x1 уравнение регрессии имеет вид 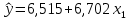 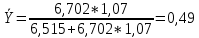 При росте фактора «Удельный вес рабочих в составе ППП» (X1) на 1%, рентабельность (Y) увеличивается на 0,49%. Частные коэффициенты эластичности находятся по формулам 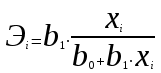 . .Расчеты эластичности приведены итоговой таблице 2. Таблица 2.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||